本文主要是介绍1125和855最小公倍数C语言,2017年事业单位行测数量关系备考之最大公约数和最小公倍数...,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
最大公约数和最小公倍数是行测数量关系里的常考考点,要做这部分题目必须掌握最大公约数和最小公倍数的概念以及解题方法,下面我们就一起学习一下这类题目的解法。
一、基本概念
1.约数、倍数
如果一个自然数a能被自然数b整除,那么称a为b的倍数,b为a的约数。
2.公约数、公倍数
如果一个自然数同时是若干个自然数的约数,那么称这个自然数是这若干个自然数的公约数。
如果一个自然数同时是若干个自然数的倍数,那么称这个自然数是这若干个自然数的公倍数。
3.最大公约数、最小公倍数
若干个数的公约数中最大的一个就称为这若干个自然数的最大公约数。
若干个数的公倍数中最小的一个就称为这若干个自然数的最小公倍数。
二、解题方法
分解质因数:
求最大公约数时,先将各数分解质因数,再将相同的质因数取幂指数最小值连乘到一起。
求最小公倍数时,先把这几个数分解质因数,再将所有的质因数取幂指数最大值连乘到一起,得到的就是这几个数的最小公倍数。
三、例题精讲
例1.一张长方形纸,长2703厘米,宽1113厘米,要把它截成若干个同样大小的正方形,纸张不能有剩余且正方形的边长要尽可能大。问:这样的正方形的边长是多少厘米?
A.153 B.156 C.158 D.159
解析:根据题意,正方形的边长是2703和1113的公约数,并且是最大公约数,利用分解质因数的方法,可以求出159是两者的最大公约数,选D选项。
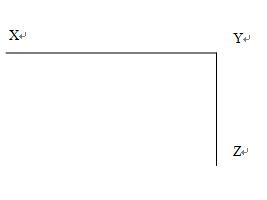
例2.如下图,街道XYZ在Y处拐弯,XY=1125米,YZ=855米,在街道一侧等距装路灯,要求XYZ处各装一盏灯,这条街道最少要按多少盏路灯?
A.47
B.46
C.45
D.44
解析:要使XYZ处各装一盏路灯,则间距应为1125,855的公约数,要使路灯最少,则应为最大公约数,可求得1125和855最大公约数是45,即间距为45米,所以路灯数为(1125+855)÷45+1=45盏,选择C选项。
例3.甲乙丙丁四个人去图书馆借书,甲每隔5天去一次,乙每隔11天去一次,丙每隔17天去一次,丁每隔29天去一次。如果5月18日他们四个人在图书馆相遇,问下一次四个人在图书馆相遇是几月几号?
A.10月18日B.10月14日C.11月18日D.11月14日
解析:每隔5、11、17、29天去一次,即每(5+1)、(11+1)、(17+1)、(29+1)天去一次,再次相遇经过的天数为6、12、18、30的最小公倍数180。则180天后四人再次相遇,这天为11月14日,选择D选择。
通过上面的讨论,大家可以看出,这种题目掌握了概念和方法以后,仔细题目,可以很快的得出正确答案。
这篇关于1125和855最小公倍数C语言,2017年事业单位行测数量关系备考之最大公约数和最小公倍数...的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





