本文主要是介绍python股票_实战 | 用 Python 选股票,据说可以多挣个20%,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
原标题:实战 | 用 Python 选股票,据说可以多挣个20%
本文将使用Python来可视化股票数据,比如绘制K线图,并且探究各项指标的含义和关系,最后使用移动平均线方法初探投资策略。
数据导入
这里将股票数据存储在stockData.txt文本文件中,我们使用pandas.read_table()函数将文件数据读入成DataFrame格式。
其中参数usecols=range(15)限制只读取前15列数据,parse_dates=[0]表示将第一列数据解析成时间格式,index_col=0则将第一列数据指定为索引。
import pandasaspd
import numpyasnp
importmatplotlib.pyplotasplt
%matplotlibinline
%configInlineBackend.figure_format='retina'
%pylabinline
pylab.rcParams['figure.figsize']=(10,6)#设置绘图尺寸
#读取数据
stock=pd.read_table('stockData.txt',usecols=range(15),parse_dates=[0],index_col=0)
stock=stock[::-1]#逆序排列
stock.head()
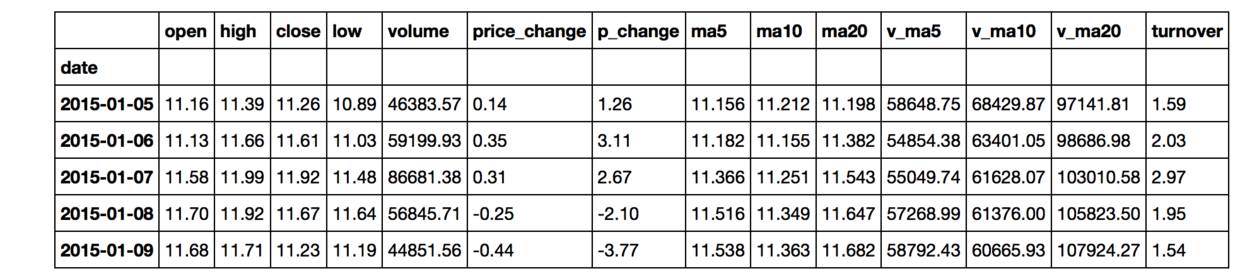
以上显示了前5行数据,要得到数据的更多信息,可以使用.info()方法。它告诉我们该数据一共有20行,索引是时间格式,日期从2015年1月5日到2015年1月30日。总共有14列,并列出了每一列的名称和数据格式,并且没有缺失值。
stock.info()
DatetimeIndex:20entries,2015-01-05to2015-01-30
Data columns(total14columns):
open20non-null float64
high20non-null float64
close20non-null float64
low20non-null float64
volume20non-null float64
price_change20non-null float64
p_change20non-null float64
ma520non-null float64
ma1020non-null float64
ma2020non-null float64
v_ma520non-null float64
v_ma1020non-null float64
v_ma2020non-null float64
turnover20non-null float64
dtypes:float64(14)
memoryusage:2.3KB
在观察每一列的名称时,我们发现’open’的列名前面似乎与其它列名不太一样,为了更清楚地查看,使用.columns得到该数据所有的列名如下:
stock.columns
Index([' open','high','close','low','volume','price_change',
'p_change','ma5','ma10','ma20','v_ma5','v_ma10','v_ma20',
'turnover'],
dtype='object')
于是发现’open’列名前存在多余的空格,我们使用如下方法修正列名。
stock.rename(columns={' open':'open'}, inplace=True)
至此,我们完成了股票数据的导入和清洗工作,接下来将使用可视化的方法来观察这些数据。
数据观察
首先,我们观察数据的列名,其含义对应如下:
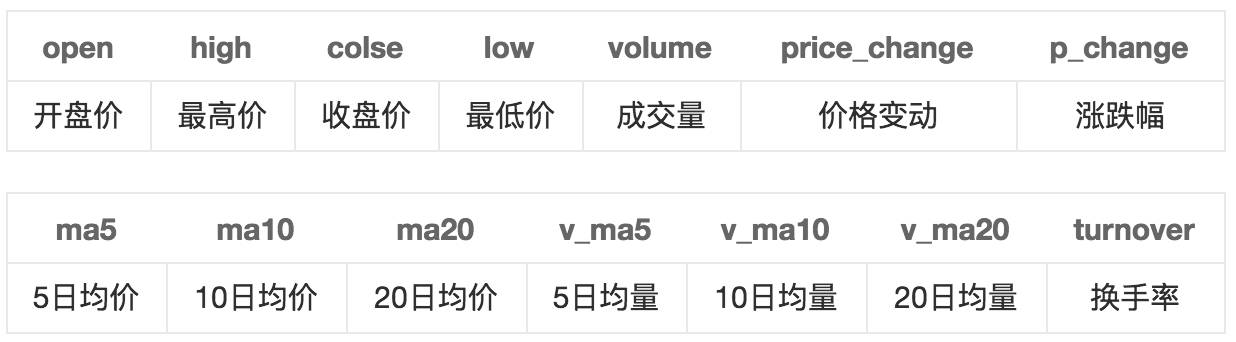
这些指标总体可分为两类:
价格相关指标
当日价格:开盘、收盘价,最高、最低价
价格变化:价格变动和涨跌幅
均价:5、10、20日均价
成交量相关指标
成交量
换手率:成交量/发行总股数×100%
成交量均量:5、10、20日均量
由于这些指标都是随时间变化的,所以让我们先来观察它们的时间序列图。
时间序列图
以时间为横坐标,每日的收盘价为纵坐标,做折线图,可以观察股价随时间的波动情况。这里直接使用DataFrame数据格式自带的做图工具,其优点是能够快速做图,并自动优化图形输出形式。
stock['close'].plot(grid=True)
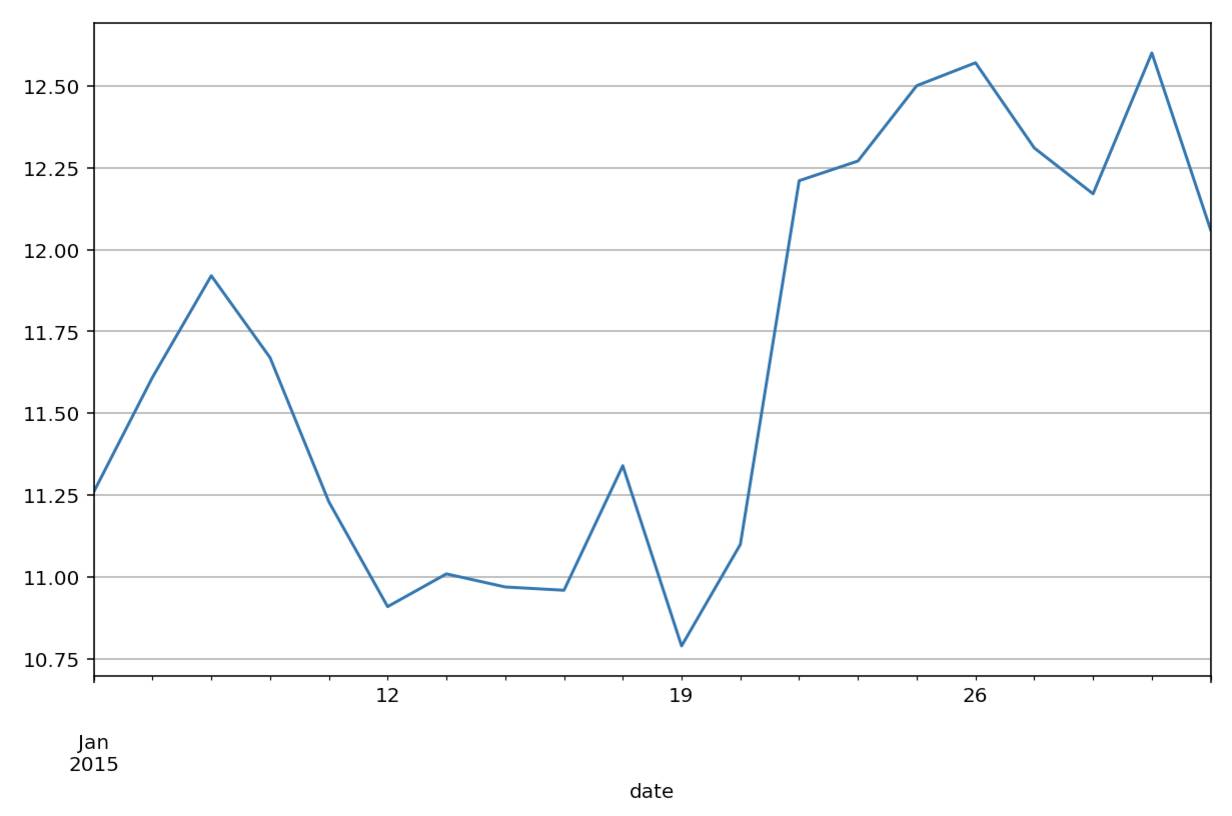
如果我们将每日的开盘、收盘价和最高、最低价以折线的形式绘制在一起,难免显得凌乱,也不便于分析。那么有什么好的方法能够在一张图中显示出这四个指标?答案下面揭晓。
K线图
相传K线图起源于日本德川幕府时代,当时的商人用此图来记录米市的行情和价格波动,后来K线图被引入到股票市场。每天的四项指标数据用如下蜡烛形状的图形来记录,不同的颜色代表涨跌情况。
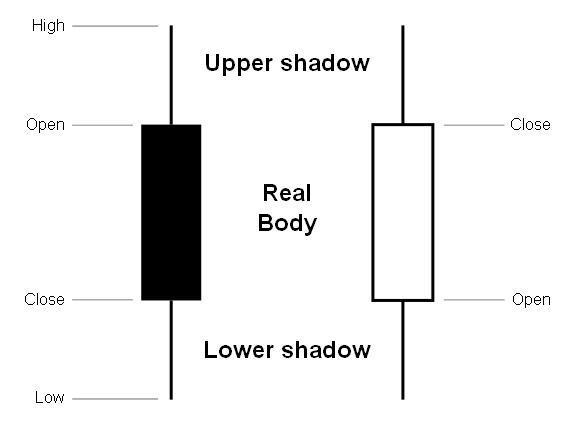
图片来源:http://wiki.mbalib.com/wiki/K线理论
Matplotlib.finance模块提供了绘制K线图的函数candlestick_ohlc(),但如果要绘制比较美观的K线图还是要下点功夫的。下面定义了pandas_candlestick_ohlc()函数来绘制适用于本文数据的K线图,其中大部分代码都是在设置坐标轴的格式。
frommatplotlib.financeimportcandlestick_ohlc
frommatplotlib.datesimportDateFormatter,WeekdayLocator,DayLocator,MONDAY
defpandas_candlestick_ohlc(stock_data,otherseries=None):
# 设置绘图参数,主要是坐标轴
mondays=WeekdayLocator(MONDAY)
alldays=DayLocator()
dayFormatter=DateFormatter('%d')
fig,ax=plt.subplots()
fig.subplots_adjust(bottom=0.2)
ifstock_data.index[-1]-stock_data.index[0]
weekFormatter=DateFormatter('%b %d')
ax.xaxis.set_major_locator(mondays)
ax.xaxis.set_minor_locator(alldays)
else:
weekFormatter=DateFormatter('%b %d, %Y')
ax.xaxis.set_major_formatter(weekFormatter)
ax.grid(True)
# 创建K线图
stock_array=np.array(stock_data.reset_index()[['date','open','high','low','close']])
stock_array[:,0]=date2num(stock_array[:,0])
candlestick_ohlc(ax,stock_array,colorup="red",colordown="green",width=0.4)
# 可同时绘制其他折线图
ifotherseriesisnotNone:
foreachinotherseries:
plt.plot(stock_data[each],label=each)
plt.legend()
ax.xaxis_date()
ax.autoscale_view()
plt.setp(plt.gca().get_xticklabels(),rotation=45,horizontalalignment='right')
plt.show()
pandas_candlestick_ohlc(stock)
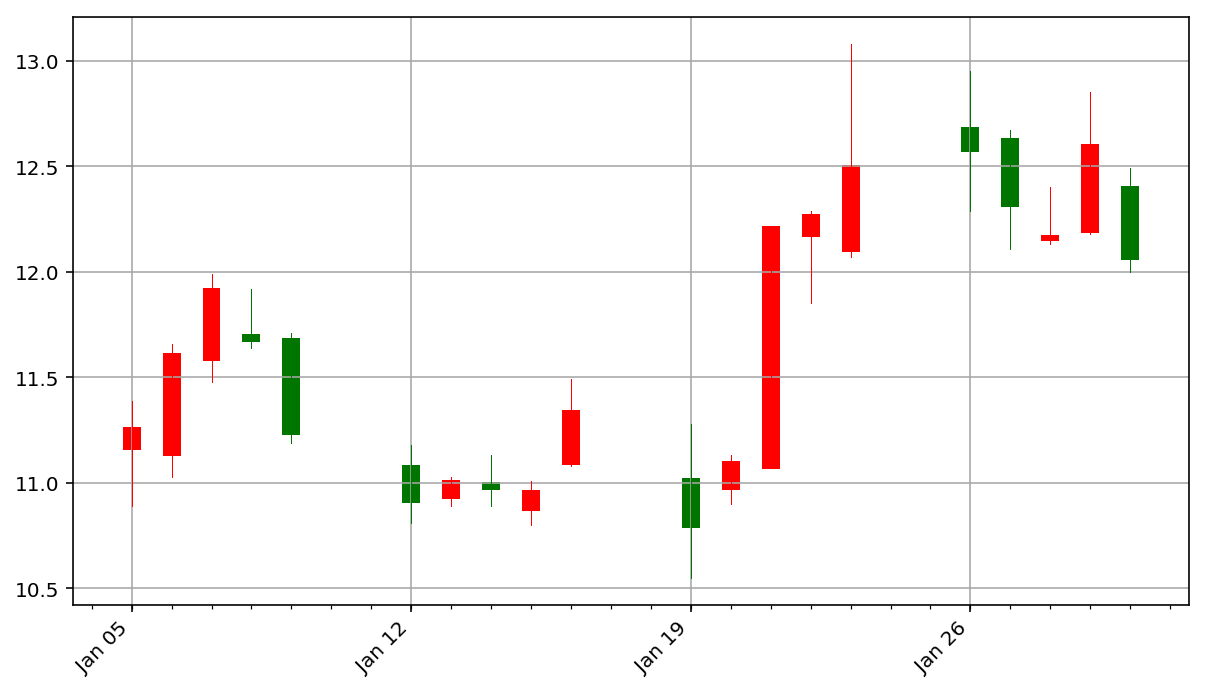
这里红色代表上涨,绿色代表下跌。
相对变化量
股票中关注的不是价格的绝对值,而是相对变化量。有多种方式可以衡量股价的相对值,最简单的方法就是将股价除以初始时的价格。

stock['return']=stock['close']/stock.close.iloc[0]
stock['return'].plot(grid=True)
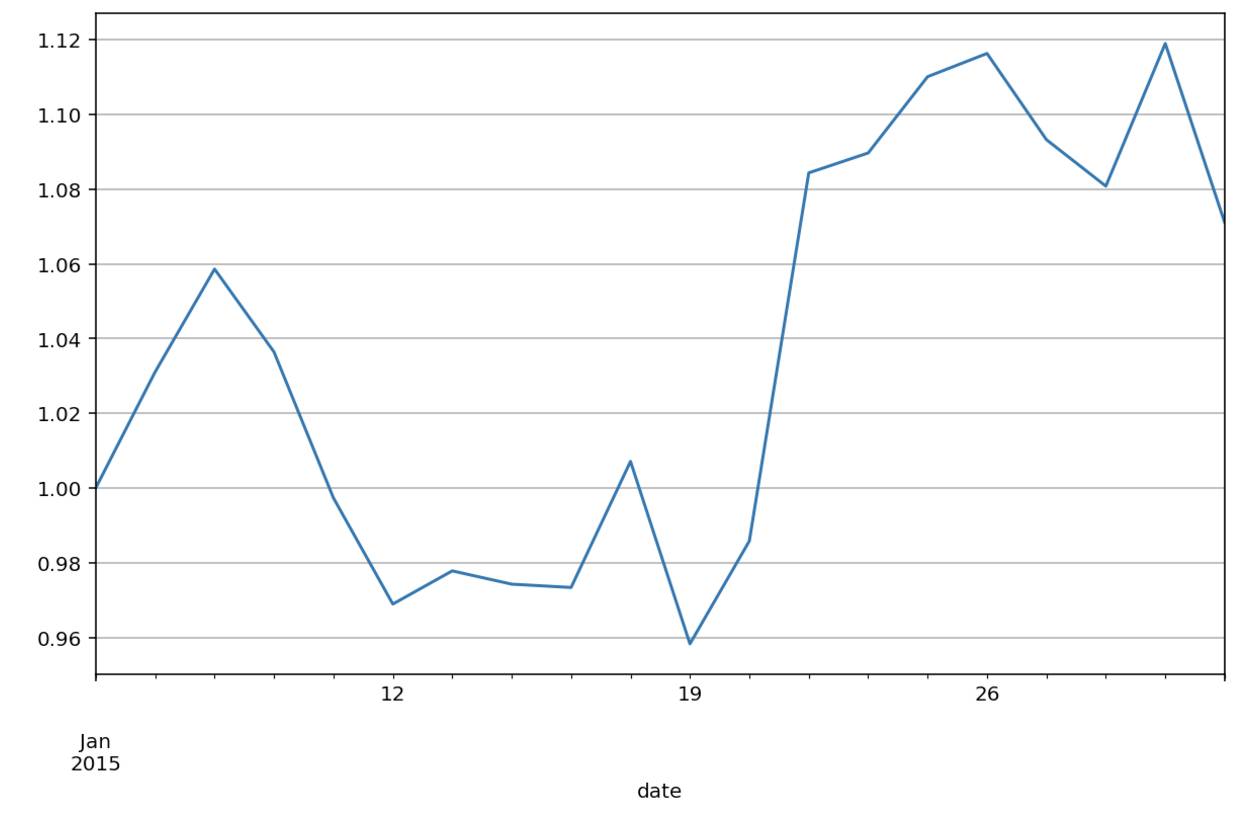
第二种方法是计算每天的涨跌幅,但计算方式有两种:
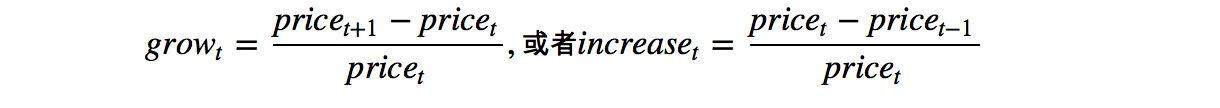
这两者可能导致不同的分析结果,样例数据中的涨跌幅使用的是第一个公式,并乘上了100%。
stock['p_change'].plot(grid=True).axhline(y=0, color='black', lw=2)
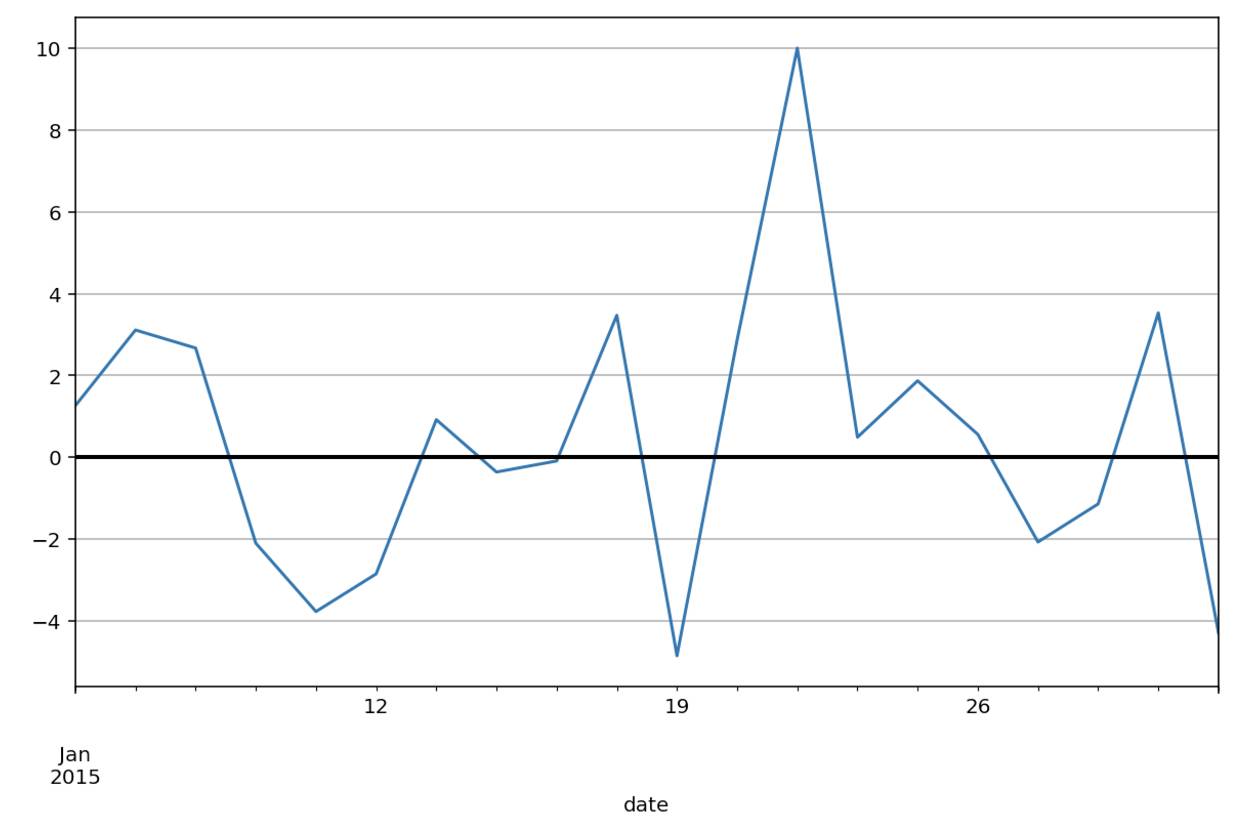
为了解决第二种方法中的两难选择,我们引入第三种方法,就是计算价格的对数之差,公式如下:
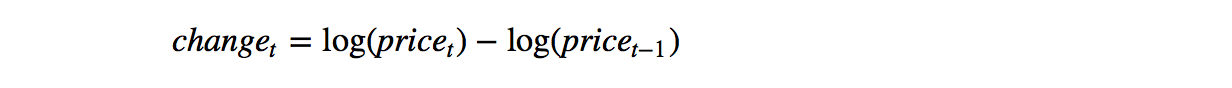
close_price=stock['close']
log_change=np.log(close_price)-np.log(close_price.shift(1))
log_change.plot(grid=True).axhline(y=0,color='black',lw=2)
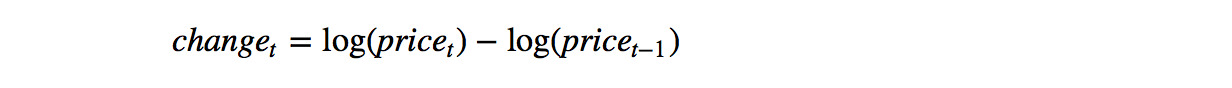
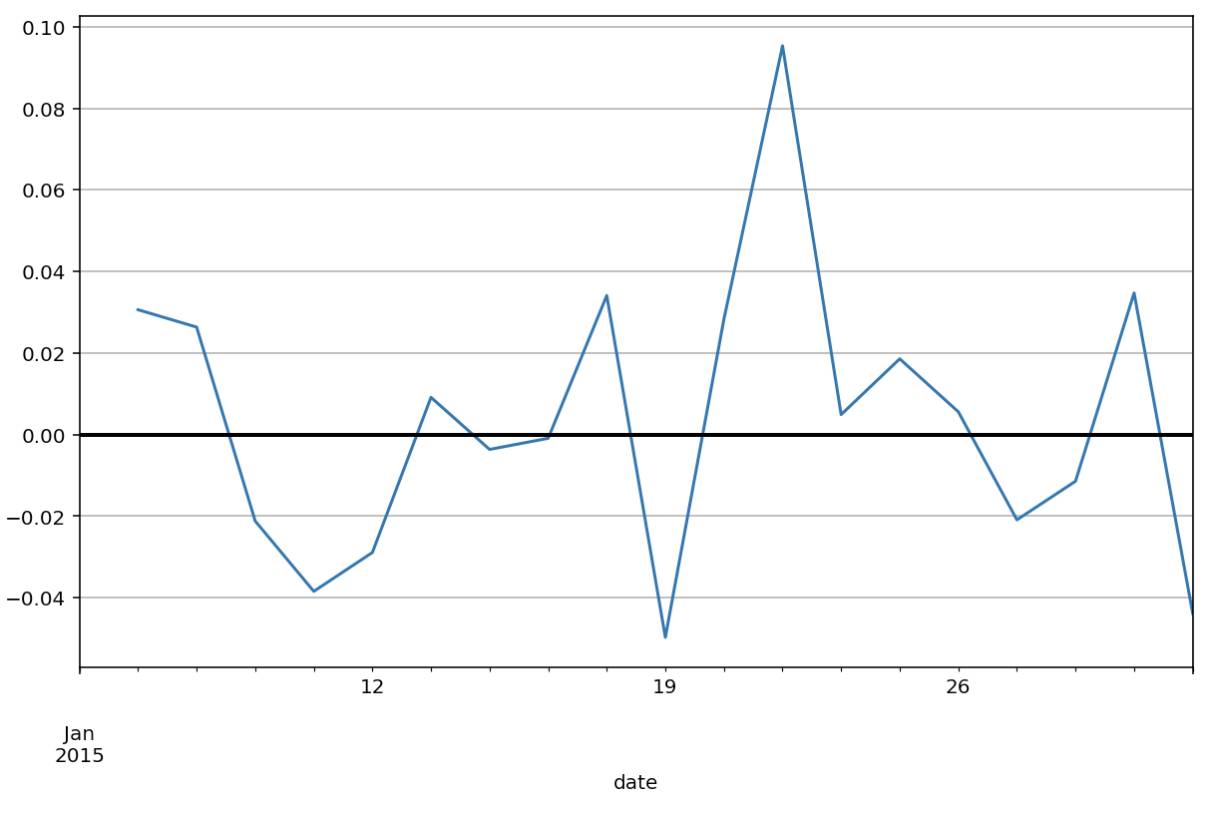
相关关系
在观察了价格的走势之后,我们来看看各指标之间的关系。下面挑选了部分代表性的指标,并使用pandas.scatter_matrix()函数,将各项指标数据两两关联做散点图,对角线是每个指标数据的直方图。
small=stock[['close','price_change','ma20','volume','v_ma20','turnover']]
_=pd.scatter_matrix(small)
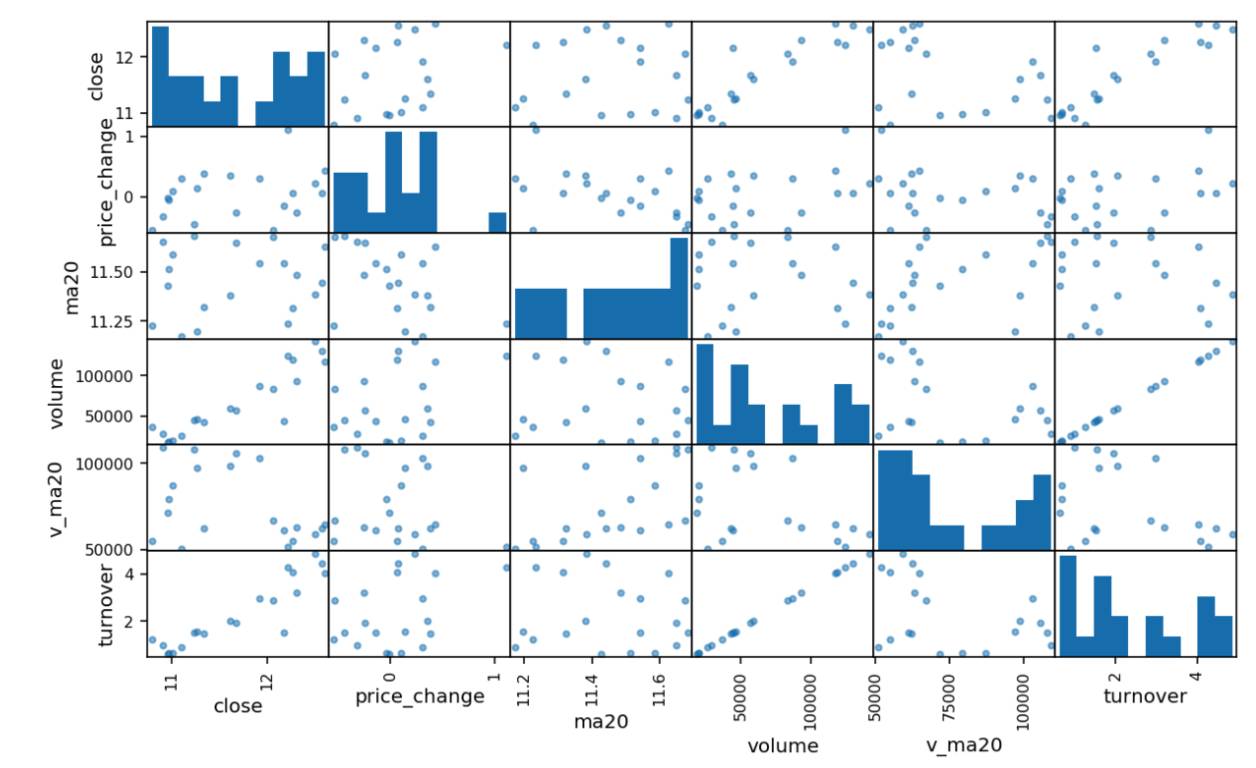
图中可以明显发现成交量(volume)和换手率(turnover)有非常明显的线性关系,其实换手率的定义就是:成交量除以发行总股数,再乘以100%。所以下面的分析中我们将换手率指标去除,这里使用了相关性关系来实现数据降维。
上面的散点图看着有些眼花缭乱,我们可以使用numpy.corrcof()来直接计算各指标数据间的相关系数。
small=stock[['close','price_change','ma20','volume','v_ma20']]
cov=np.corrcoef(small.T)
cov
array([[1.,0.30308764,0.10785519,0.91078009,-0.37602193],
[0.30308764,1.,-0.45849273,0.3721832,-0.25950305],
[0.10785519,-0.45849273,1.,-0.06002202,0.51793654],
[0.91078009,0.3721832,-0.06002202,1.,-0.37617624],
[-0.37602193,-0.25950305,0.51793654,-0.37617624,1.]])
如果觉得看数字还是不够方便,我们继续将上述相关性矩阵转换成图形,如下图所示,其中用颜色来代表相关系数。我们发现位于(0,3)位置的相关系数非常大,查看数值达到0.91。这两个强烈正相关的指标是收盘价和成交量。
img=plt.matshow(cov,cmap=plt.cm.winter)
plt.colorbar(img,ticks=[-1,0,1])
plt.show()
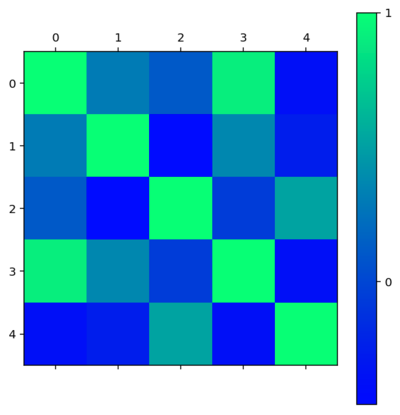
以上我们用矩阵图表的方式在多个指标中迅速找到了强相关的指标。接着做出收盘价和成交量的折线图,因为它们的数值差异很大,所以我们采用两套纵坐标体系来做图。
stock[['close','volume']].plot(secondary_y='volume', grid=True)
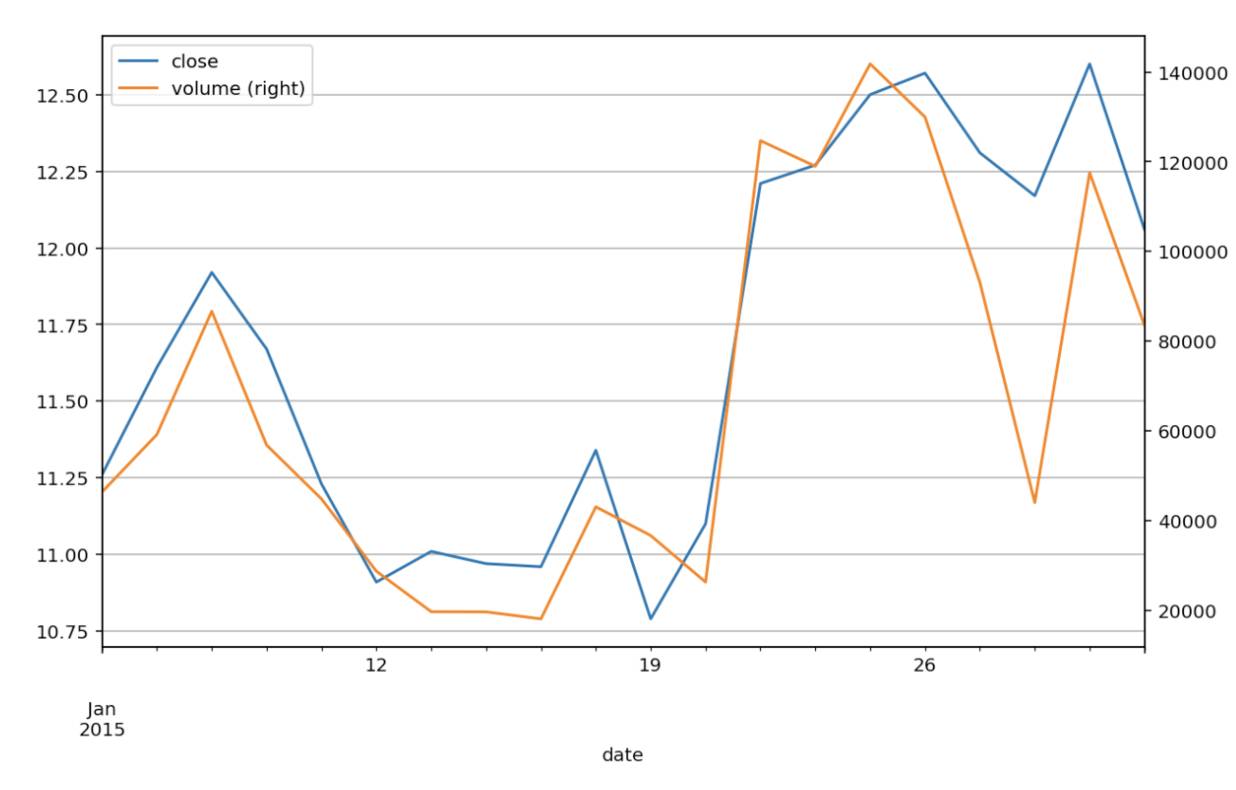
观察这两个指标的走势,在大部分时候股价上涨,成交量也上涨,反之亦然。但个别情况下则不成立,可能是成交量受到前期的惯性影响,或者还有其他因素。
移动平均线
吴军老师曾讲述他的投资经验,大意是说好的投资方式不是做预测,而是能在合适的时机做出合适的应对和决策。同样股市也没法预测,我们能做的是选择恰当的策略应对不同的情况。
好的指标是能驱动决策的。在上面的分析中我们一直没有使用的一类指标是5、10、20日均价,它们又称为移动平均值,下面我们就使用这项指标来演示一个简单的股票交易策略。(警告:这里仅仅是演示说明,并非投资建议。)
为了得到更多的数据来演示,我们使用pandas_datareader直接从雅虎中下载最近一段时间的谷歌股票数据。
import datetime
importpandas_datareader.dataasweb
# 设置股票数据的时间跨度
start=datetime.datetime(2016,10,1)
end=datetime.date.today()
# 从yahoo中获取google的股价数据。
goog=web.DataReader("GOOG","yahoo",start,end)
#修改索引和列的名称,以适应本文的分析
goog.index.rename('date',inplace=True)
goog.rename(columns={'Open':'open','High':'high','Low':'low','Close':'close'},inplace=True)
goog.head()
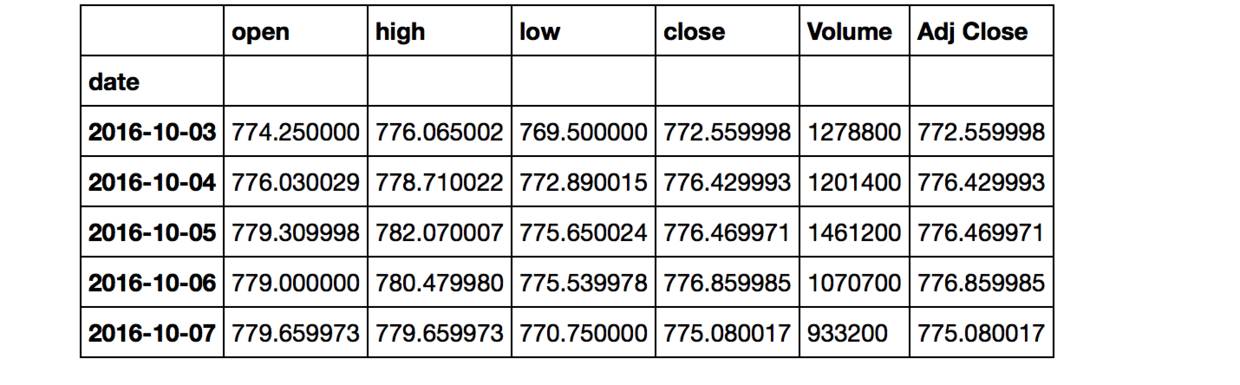
数据中只有每天的价格和成交量,所以我们需要自己算出5日均价和10日均价,并将均价的折线图(也称移动平均线)与K线图画在一起。
goog["ma5"]=np.round(goog["close"].rolling(window=5,center=False).mean(),2)
goog["ma20"]=np.round(goog["close"].rolling(window=20,center=False).mean(),2)
goog=goog['2017-01-01':]
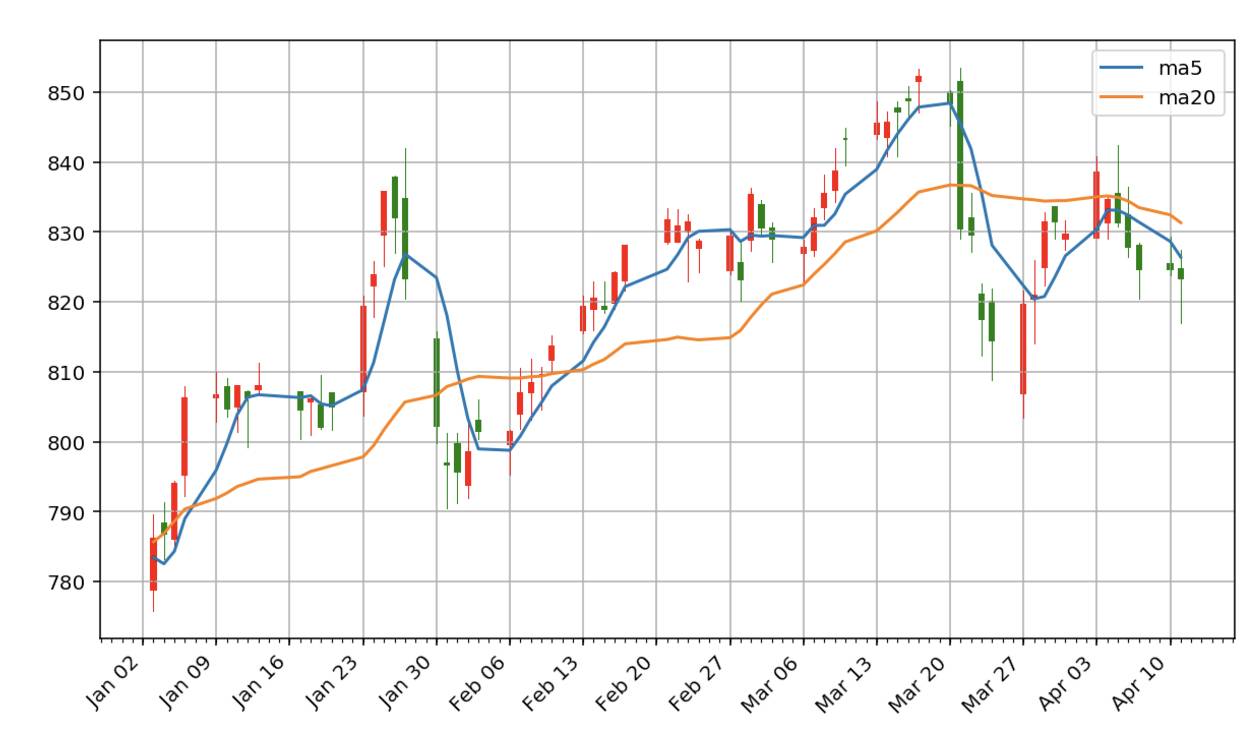
pandas_candlestick_ohlc(goog,['ma5','ma20'])
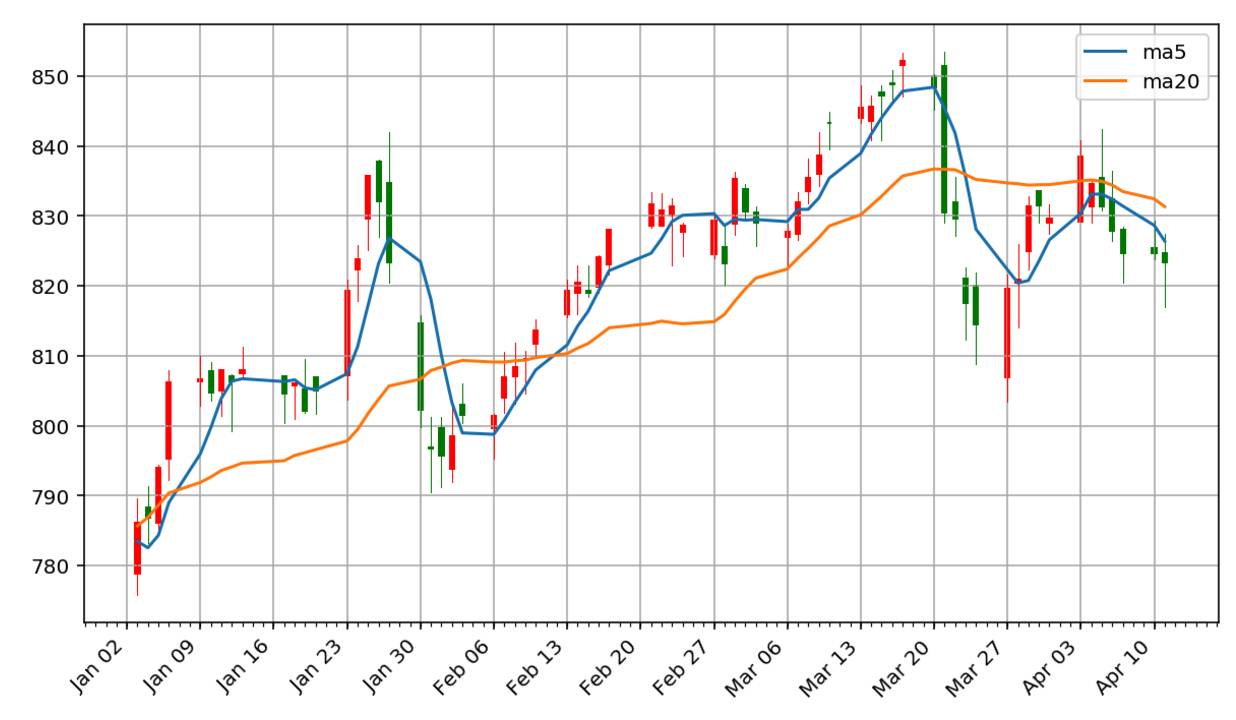
观察上图,我们发现5日均线与K线图较为接近,而20日均线则更平坦,可见移动平均线具有抹平短期波动的作用,更能反映长期的走势。比较5日均线和20日均线,特别是关注它们的交叉点,这些是交易的时机。移动平均线策略,最简单的方式就是:当5日均线从下方超越20日均线时,买入股票,当5日均线从上方越到20日均线之下时,卖出股票。
为了找出交易的时机,我们计算5日均价和20日均价的差值,并取其正负号,作于下图。当图中水平线出现跳跃的时候就是交易时机。
goog['ma5-20']=goog['ma5']-goog['ma20']
goog['diff']=np.sign(goog['ma5-20'])
goog['diff'].plot(ylim=(-2,2)).axhline(y=0,color='black',lw=2)
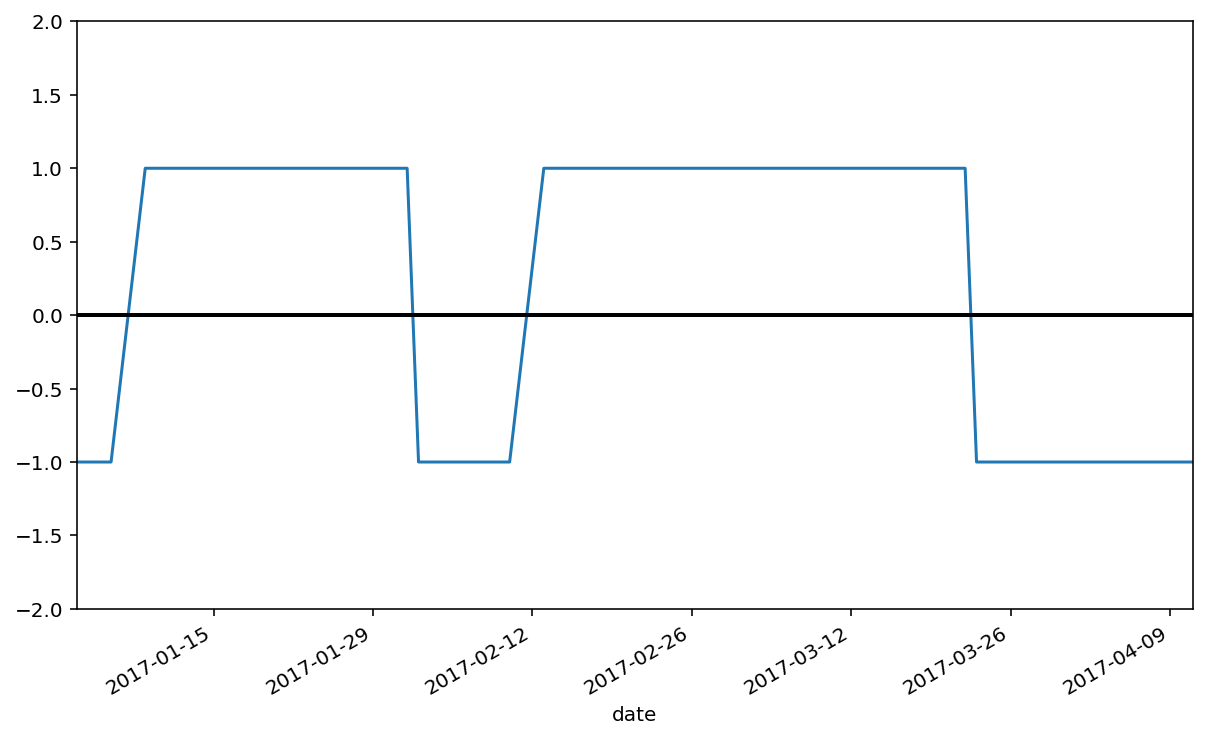
为了更方便观察,上述计算得到的均价差值,再取其相邻日期的差值,得到信号指标。当信号为1时,表示买入股票;当信号为-1时,表示卖出股票;当信号为0时,不进行任何操作。
goog['signal']=np.sign(goog['diff']-goog['diff'].shift(1))
goog['signal'].plot(ylim=(-2,2))
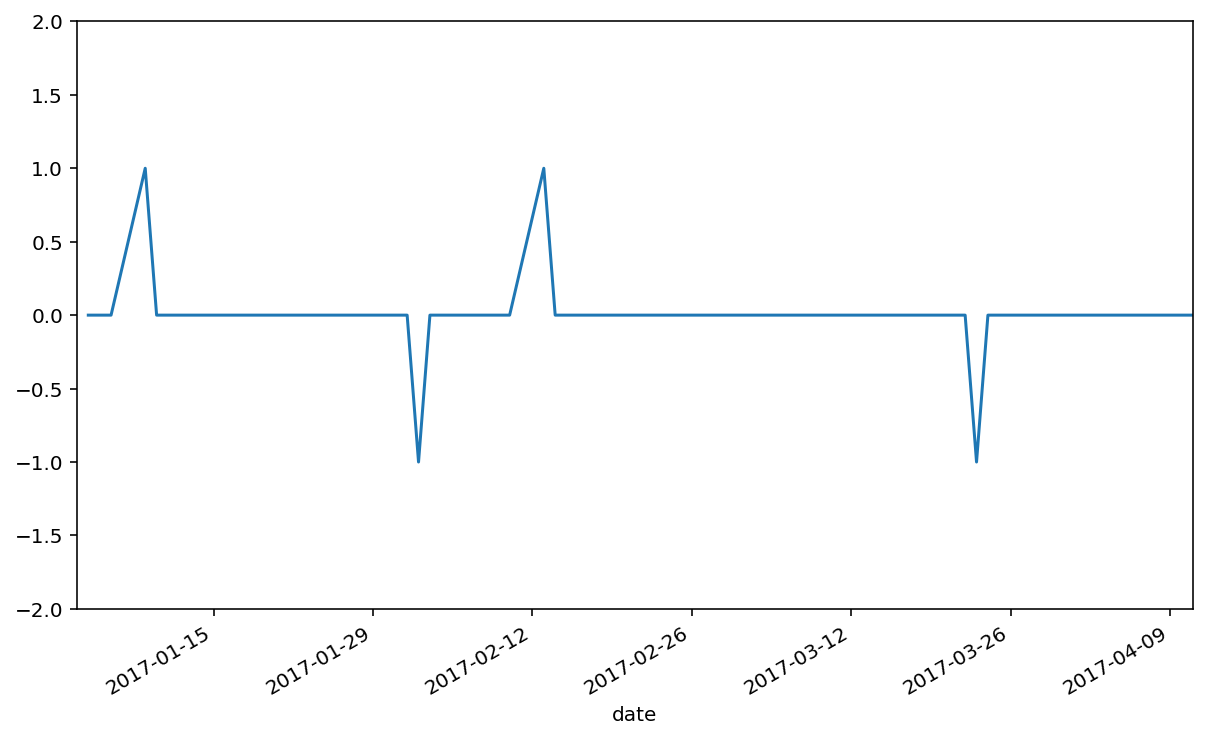
从上图中看出,从今年初到现在,一共有两轮买进和卖出的时机。到目前为止,似乎一切顺利,那么让我们看下这两轮交易的收益怎么样吧。
trade=pd.concat([
pd.DataFrame({"price":goog.loc[goog["signal"]==1,"close"],
"operation":"Buy"}),
pd.DataFrame({"price":goog.loc[goog["signal"]== -1,"close"],
"operation":"Sell"})
])
trade.sort_index(inplace=True)
trade
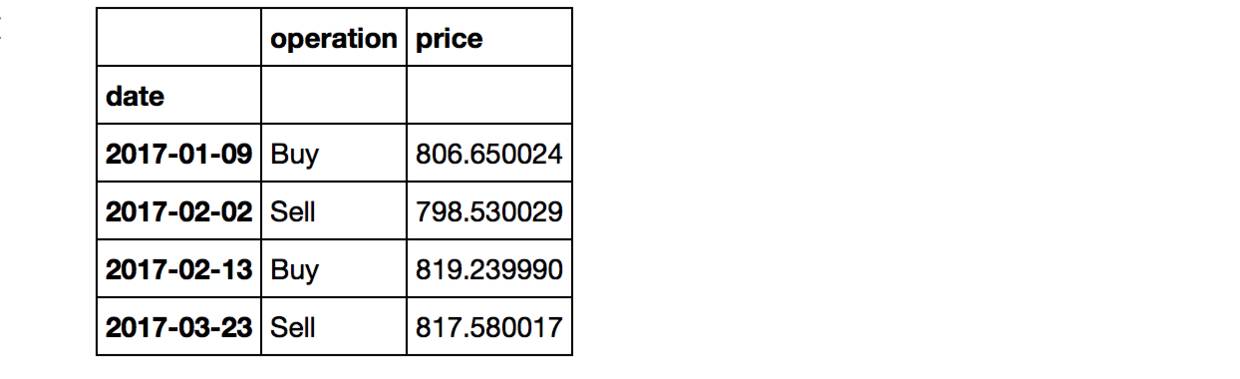
上述表格列出了交易日期、操作和当天的价格。但很遗憾地发现,这两轮交易的卖出价都小于买入价,实际上按上述方法交易我们亏本了!!!
你是否很愤怒呢?原来分析到现在,都是假的呀!我之前就警告过,这里的分析只是演示移动平均线策略的思想,而并非真正的投资建议。股票市场是何其的复杂多变,又如何是一个小小的策略所能战胜的呢?
那么这个策略就一无是处吗?非也!如果考虑更长的时间跨度,比如5年、10年,并考虑更长的均线,比如将20日均线和50日均线比较;虽然过程中也有亏损的时候,但赢的概率更大。也就是说,在更长的时间尺度上该策略也是可行的。但即使你赚了,又能跑赢大盘吗?这时候还需用到其他方法,比如合理配置投资比例等。
还是那句话,股市有风险,投资需谨慎。本文不是分析股票的文章,而是借用股票数据来说明数据分析的基本方法,以及演示什么样的指标是好的指标。
参考资料:
An Introduction to Stock Market Data Analysis with Python (Part 1)
An Introduction to Stock Market Data Analysis with Python (Part 2)
K线理论
K线图做图示例
来源:鱼心DrFish
www.jianshu.com/p/ce0e0773c6ec#返回搜狐,查看更多
责任编辑:
这篇关于python股票_实战 | 用 Python 选股票,据说可以多挣个20%的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






