拓扑排序——平行课程（leetcode 1136）

题目描述

已知有 N 门课程，它们以 1 到 N 进行编号。

给你一份课程关系表 relations[i] = [X, Y]，用以表示课程 X 和课程 Y 之间的先修关系：课程 X 必须在课程 Y 之前修完。

假设在一个学期里，你可以学习任何数量的课程，但前提是你已经学习了将要学习的这些课程的所有先修课程。

请你返回学完全部课程所需的最少学期数。

如果没有办法做到学完全部这些课程的话，就返回 -1。

示例 1：

输入：N = 3, relations = [[1,3],[2,3]]
输出：2
解释：
在第一个学期学习课程 1 和 2，在第二个学期学习课程 3。

示例 2：

输入：N = 3, relations = [[1,2],[2,3],[3,1]]
输出：-1
解释：
没有课程可以学习，因为它们相互依赖。

提示：

    1 <= N <= 5000
    1 <= relations.length <= 5000
    relations[i][0] != relations[i][1]
    输入中没有重复的关系

算法分析

根据题目的描述和示例，我们首先应该想到本题很适合图的算法。那么我们就以图的形式将题目中的信息建模。

    令 G(V,E)G(V, E)G(V,E) 为一个有向，无权图。
    每门课程为图中的一个结点。
    根据课程之间的先修关系对边进行建模。问题中给出的 relations[i] = [X, Y] 的二元组代表课程 X 是课程 Y 的先修课程。这可以用一条有向边表示。
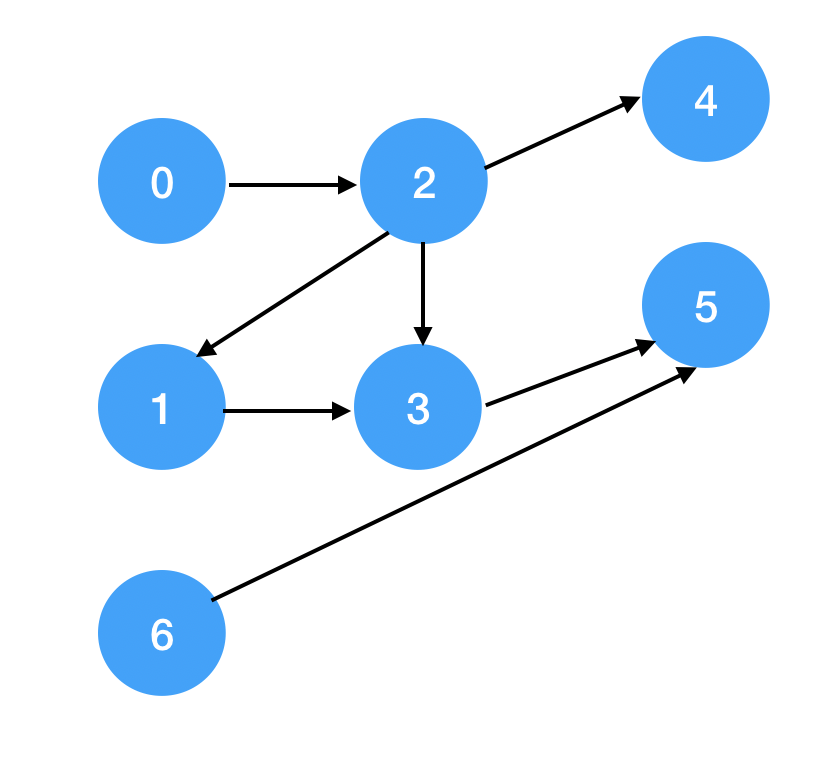
    图 GGG 有可能是循环图，如果是循环图，则不可能完成所以课程。

下面我们根据一个示例来建图，示例为 relations = [[0,2],[1,3],[2,1],[2,3],[2,4],[3,5],[6,5]。

对于上述图，可能的一种上课方法是：0 6 2 1 4 3 5，还有一种可能的方法为：0 2 1 3 4 5 6。当然还有其他可能的方法。这是两种不同的排序方法，第一种是根据拓扑排序，第二种则是深度优先遍历的方法。本题使用第一种方法更加合适。
方法一：拓扑排序

思路

这题其实是典型的有优先级限制的调度问题，我们可以使用拓扑排序来解决这样的问题。

我们知道只有当一门课程没有前置课程的时候，才能上这门课。我们可以把这门课程需要上的前置课程的数量表示为入度。比如上图中 0 的入度为 0，没有前置课程需要上，而 3 的入度为 2，有 1 和 2 需要上。所以我们可以每一次遍历把所有入度为 0 的课程上完，并且把他们的后置课程的入度减 1，重复这个过程直到没有课程可以上。

算法

    初始化所有课程的入度 preClassCount和直接后置课程 nextClasses。
    初始化 term 记录一共遍历了几次，一次代表一个学期。
    找出所有入度为 0 的课程，记录为已学习 learn。
    将所有这学期已学习的课程的直接后置课程的入度减 1。
    重复第三步直到所有课程已经学完，或者这个学期不能学习任何课程。

广度优先搜索

class Solution {
public:int minimumSemesters(int n, vector<vector<int>>& relations) {vector<vector<int>> edges(n);vector<int> ins(n);queue<int> que;for(auto& v : relations) {edges[v[0]-1].push_back(v[1]-1);++ins[v[1]-1];}for(int i =0; i < n; ++i) {if(ins[i] == 0) {que.push(i);}}int ans = 0;int count = 0;while(!que.empty()) {int size = que.size();++ans;while(size) {--size;int v = que.front();que.pop();count++;for(auto& neighbor : edges[v]) {--ins[neighbor];if(ins[neighbor] == 0) {que.push(neighbor);}}}}return count == n? ans:-1;}
};

算法复杂度分析

时间复杂度：O(E+V)。这里 E表示邻边的条数，V表示结点的个数。初始化入度为 0 的集合需要遍历整张图，具体做法是检查每个结点和每条边，因此复杂度为 O(E+V)，然后对该集合进行操作，又需要遍历整张图中的每个结点和每条边，复杂度也为 O(E+V)。

空间复杂度：O(E+V)。这里 E 表示邻边的条数，V 表示结点的个数。入度数组长度为节点个数 V，二维数组记录后置节点的长度为 E。