【挖坑】【GSS系列】GSS1:区间最大子段和

Can you answer these queries?

​ GSS系列是spoj出品的一套数据结构好毒瘤题，主要以线段树、平衡树和树链剖分为背景，进行了一些操作的魔改，使得难度远超模板题，但对于思维有极大的提升。

​ 所以我会选择一些在我能力范围内的题挖坑选讲，构成一个GSS系列。至于剩下那些，等我成为巨佬弄懂了再说吧。

GSS1:区间最大子段和

原题传送门（洛谷）

题意

​ 给定一个序列，无修改操作，查询某一段区间的最大子段和。

口胡

​ 首先，题目要求区间查询，那么第一感觉就是使用线段树维护。那么如何维护一个区间的最大子段和呢？在线段树中，push_up和push_down操作永远是最关键的，但由于本题无修改操作，所以只需要关心push_up操作。于是考虑两个相邻区间如何合并成为一个更大的区间。（随便瞎搞一下就好了）

​ 我们设一个区间的从左端点开始的最大子段和为$ls$，同理从右端点开始为$rs$，整段区间和为$sum$，区间最大子段和为$mx$。

​ 那么一个大区间的$ls$就可以由左半区间的$ls$或左区间的$sum$加上右区间的$ls$，同理求得$rs$。$mx$可以由左右区间的$mx$和合并后中间的最大子段和（左区间的$rs$和右区间的$ls$）合并而来。

图解

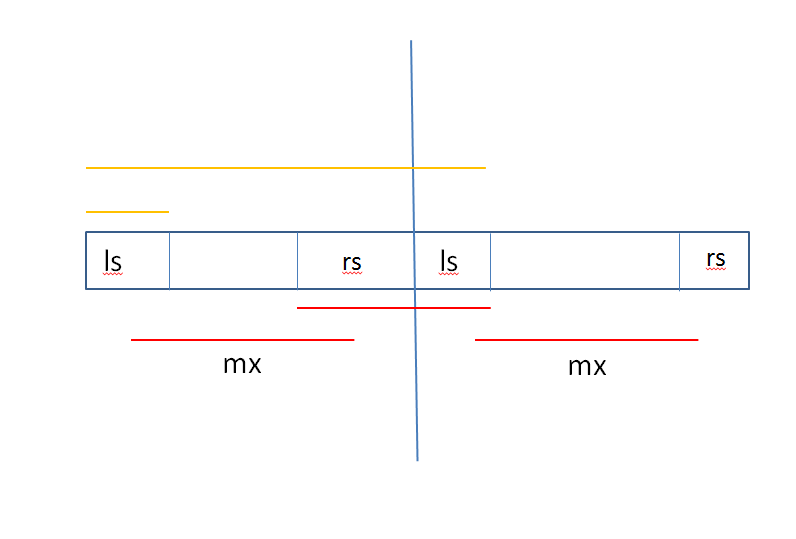
​ 如图，对于一个大区间，它的$ls$可以是上图的两条黄色线段，即

​ ls[p] = max(ls[lc(p)], sum[lc(p)]+ls[rc(p)])，同理可求得$rs$。

​ 对于区间的$mx$，显然可以是上图的三条红色线段，即

​ mx[p] = max(mx[lc(p)], mx[rc(p)], rs[lc(p)]+ls[rc(p)])。

​ 讲完了维护，接下来就是一些查询的套路了。由于我们查询的最大子段和不能仅依靠自己进行合并。所以即使我们知道了左右区间的最大子段和，也不能立马得出当前区间的最大子段和。所以我们选择在查询的时候直接返回一个节点。这样就可以获取到所有子区间的信息，再通过上述方法合并就可得到最后的答案。

代码：

#include <bits/stdc++.h>
#define MAXN 50005
#define lc(x) (x<<1)
#define rc(x) (x<<1|1)
#define mid ((l+r)>>1)
using namespace std;struct node{int sum, ls, rs, ms;		//区间和,分别从左右端点开始的最大子段和,区间最大子段和 
};int n, m, val[MAXN];
node a[MAXN*4];void push_up(int p){			//将子区间合并到父亲区间a[p].sum = a[lc(p)].sum + a[rc(p)].sum;a[p].ls = max(a[lc(p)].ls, a[lc(p)].sum+a[rc(p)].ls);a[p].rs = max(a[rc(p)].rs, a[rc(p)].sum+a[lc(p)].rs);a[p].ms = max(max(a[lc(p)].ms, a[rc(p)].ms), a[lc(p)].rs + a[rc(p)].ls);
}void build(int p, int l, int r){if(l == r){a[p].sum = a[p].ls = a[p].rs = a[p].ms = val[l];return;}build(lc(p), l, mid);build(rc(p), mid+1, r);push_up(p);
}node query(int p, int l, int r, int ul, int ur){	//返回节点所有信息if(l>=ul && r<=ur){return a[p];}if(ul > mid){		//两个特判，判断所查询的区间被当前的左或右区间包含，直接去相应子区间查询return query(rc(p), mid+1, r, ul, ur);}if(ur <= mid){return query(lc(p), l, mid, ul, ur);}node res, tl, tr;			//合并答案，具体原理看图解分析tl = query(lc(p), l, mid, ul, ur);tr = query(rc(p), mid+1, r, ul, ur);res.sum = tl.sum + tr.sum;res.ls = max(tl.ls, tl.sum+tr.ls);res.rs = max(tr.rs, tr.sum+tl.rs);res.ms = max(max(tl.ms, tr.ms), tl.rs+tr.ls);return res;
}int main()
{cin >> n;for(int i = 1; i <= n; i++){scanf("%d", &val[i]);}build(1, 1, n);cin >> m;int x, y;while(m--){scanf("%d%d", &x, &y);printf("%d\n", query(1,1,n, x, y).ms);}return 0;
}

What to do next?

​ GSS3: 带单点修改的最大子段和

​ 其实在真正了解了区间最大子段和求法之后，即使是带修改，也并没有增加任何难度，因为实际上修改并不影响任何最大子段和的性质，无非多加一个普通的修改函数而已。