CodeForces 1293 C NEKO's Maze Game

题意：

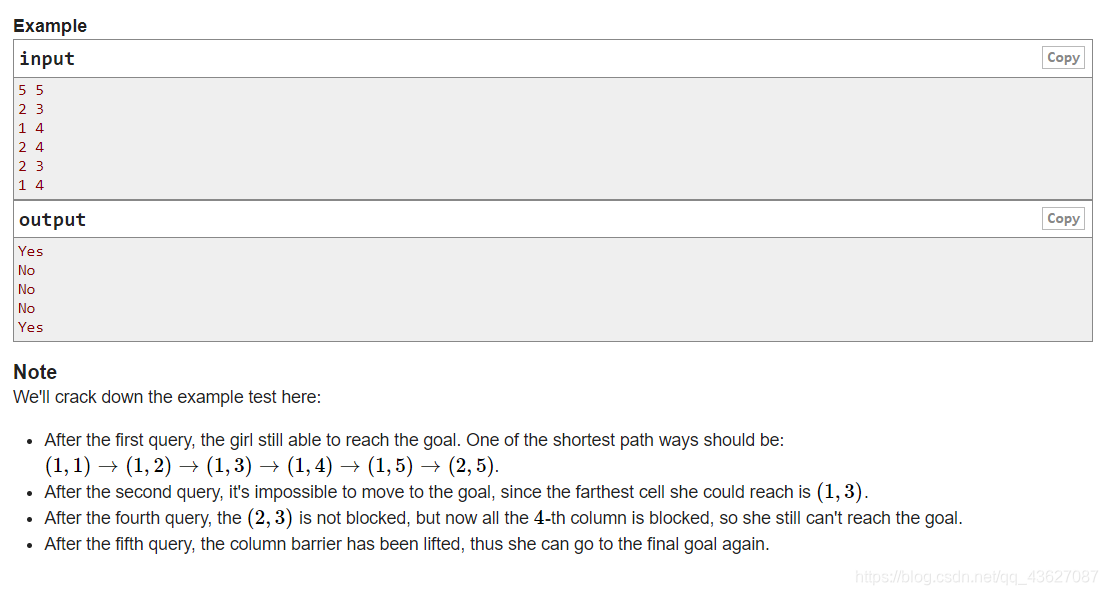
2*n的迷宫，从（1，1）出发到（2，n），初始时全部的都是地面，每次询问会把一个地面给变成熔浆，熔浆变成地面，熔浆不能通过，问是否可以走到。
每次变成熔浆的话只会对这个点对面的相邻的三个点，所以每次查询只需要判断是否对面的相邻的三个点是否都是地面就行。

AC代码：

#include <cstdio>
#include <vector>
#include <queue>
#include <cstring>
#include <cmath>
#include <map>
#include <set>
#include <string>
#include <iostream>
#include <algorithm>
#include <iomanip>
#include <stack>
#include <queue>
using namespace std;
#define sd(n) scanf("%d", &n)
#define sdd(n, m) scanf("%d%d", &n, &m)
#define sddd(n, m, k) scanf("%d%d%d", &n, &m, &k)
#define pd(n) printf("%d\n", n)
#define pc(n) printf("%c", n)
#define pdd(n, m) printf("%d %d", n, m)
#define pld(n) printf("%lld\n", n)
#define pldd(n, m) printf("%lld %lld\n", n, m)
#define sld(n) scanf("%lld", &n)
#define sldd(n, m) scanf("%lld%lld", &n, &m)
#define slddd(n, m, k) scanf("%lld%lld%lld", &n, &m, &k)
#define sf(n) scanf("%lf", &n)
#define sc(n) scanf("%c", &n)
#define sff(n, m) scanf("%lf%lf", &n, &m)
#define sfff(n, m, k) scanf("%lf%lf%lf", &n, &m, &k)
#define ss(str) scanf("%s", str)
#define rep(i, a, n) for (int i = a; i <= n; i++)
#define per(i, a, n) for (int i = n; i >= a; i--)
#define mem(a, n) memset(a, n, sizeof(a))
#define debug(x) cout << #x << ": " << x << endl
#define pb push_back
#define all(x) (x).begin(), (x).end()
#define fi first
#define se second
#define mod(x) ((x) % MOD)
#define gcd(a, b) __gcd(a, b)
#define lowbit(x) (x & -x)
typedef pair<int, int> PII;
typedef long long ll;
typedef unsigned long long ull;
typedef long double ld;
const int MOD = 1e9 + 7;
const double eps = 1e-9;
const ll INF = 0x3f3f3f3f3f3f3f3fll;
const int inf = 0x3f3f3f3f;
inline int read()
{int ret = 0, sgn = 1;char ch = getchar();while (ch < '0' || ch > '9'){if (ch == '-')sgn = -1;ch = getchar();}while (ch >= '0' && ch <= '9'){ret = ret * 10 + ch - '0';ch = getchar();}return ret * sgn;
}
inline void Out(int a) //Êä³öÍâ¹Ò
{if (a > 9)Out(a / 10);putchar(a % 10 + '0');
}ll gcd(ll a, ll b)
{return b == 0 ? a : gcd(b, a % b);
}ll lcm(ll a, ll b)
{return a * b / gcd(a, b);
}
///快速幂m^k%mod
ll qpow(ll a, ll b, ll mod)
{if (a >= mod)a = a % mod + mod;ll ans = 1;while (b){if (b & 1){ans = ans * a;if (ans >= mod)ans = ans % mod + mod;}a *= a;if (a >= mod)a = a % mod + mod;b >>= 1;}return ans;
}// 快速幂求逆元
int Fermat(int a, int p) //费马求a关于b的逆元
{return qpow(a, p - 2, p);
}///扩展欧几里得
int exgcd(int a, int b, int &x, int &y)
{if (b == 0){x = 1;y = 0;return a;}int g = exgcd(b, a % b, x, y);int t = x;x = y;y = t - a / b * y;return g;
}///使用ecgcd求a的逆元x
int mod_reverse(int a, int p)
{int d, x, y;d = exgcd(a, p, x, y);if (d == 1)return (x % p + p) % p;elsereturn -1;
}///中国剩余定理模板0
ll china(int a[], int b[], int n) //a[]为除数，b[]为余数
{int M = 1, y, x = 0;for (int i = 0; i < n; ++i) //算出它们累乘的结果M *= a[i];for (int i = 0; i < n; ++i){int w = M / a[i];int tx = 0;int t = exgcd(w, a[i], tx, y); //计算逆元x = (x + w * (b[i] / t) * x) % M;}return (x + M) % M;
}bool vis[3][100010];
int n, q, ans = 0;int main()
{sdd(n, q);int x, y, t;mem(vis, 0);while (q--){int x, y, pos;sdd(x, y);x--;pos = (x + 1) % 2;if (vis[x][y]){vis[x][y] = 0;ans = ans - vis[pos][y - 1] - vis[pos][y] - vis[pos][y + 1];}else{vis[x][y] = 1;ans = ans + vis[pos][y - 1] + vis[pos][y] + vis[pos][y + 1];}if (!ans)puts("Yes");elseputs("No");}return 0;
}