Forget-free Continual Learning with Winning Subnetworks论文阅读+代码解析

本篇文章是来自ICML2022上的一篇，而且是由之前出名的FedWEIT的团队进行研究的，因此这篇文章中也存在着相似的影子，论文地址点这里。

一. 背景（简要介绍）

持续学习又被称为增量式学习，要求不断地接受数据样本并且不会产生灾难性遗忘。最广泛的3种类型为：基于正则化的持续学习，基于记忆重塑的持续学习以及基于动态架构的持续学习。然而，上述的方法都会造成新的内存压力，特别是对于记忆重塑和动态架构。因此，现在又产生了一种基于修建的方法，如下：

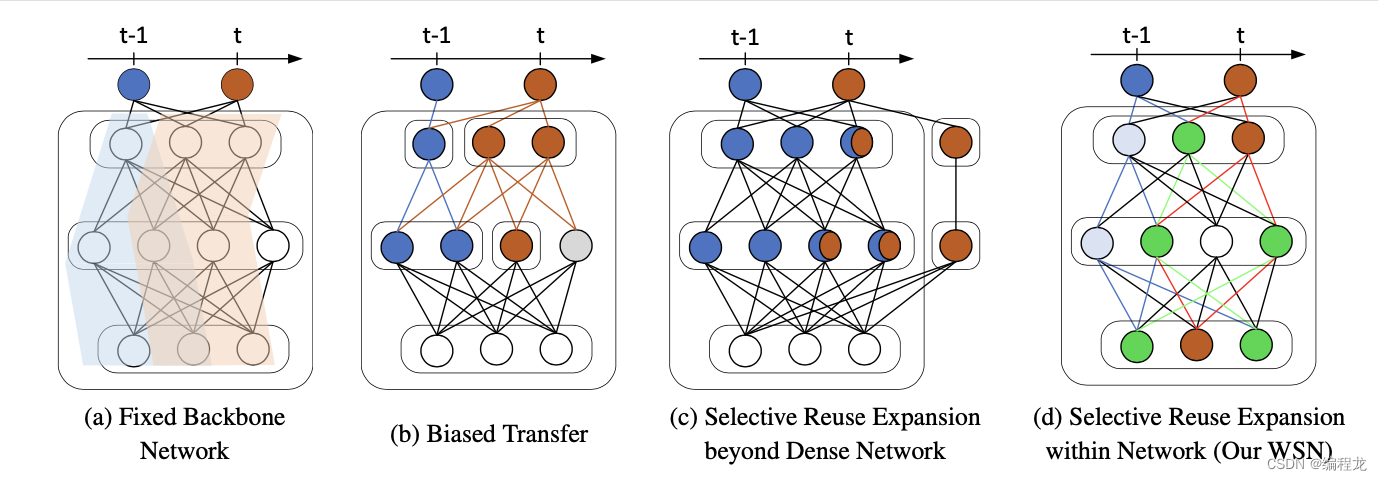
可以发现这些方法（a-c）都将模型进行了一些切分，让每个任务有对应的网络进行训练。

本文中，作者运用了彩票假设(Lottery Ticket Hypothesis)，为每一个任务考虑一个子模型进行训练。

补充：彩票假设大概意思是当一个人买了足够多的彩票之后，其中必定有一张彩票是中奖的。对应于神经网络就是，在庞大的参数面前，我们可以从中提取一部分的参数形成子网络，而这个子网络能够表现的和主网络一样好。

二. Forget-Free Continual Learning with Winning SubNetworks

问题定义： 在持续学习中，存在着$T$个任务，假设第$t$个任务的数据集表示为 D t = { x i , t , y i , t } i = 1 n t \mathcal{D}_t=\{x_{i,t},y_{i,t}\}^{n_t}_{i=1} Dt​={xi,t​,yi,t​}i=1nt​​，其中$n_t$表示对应的样本数。假设神经网络为为$f(.;\theta )$，那么在任务$t$上我们优化目标为：
$${\theta }^{\ast }=\underset{\theta }{\min }\frac{1}{n_t}\sum _{i=1}^{n_t}\mathcal{L}(f(x_{i,t};\theta ),y_{i,t})$$
为了留出学习未来任务的空间，可以找到获得同等甚至更好性能的子网络。给定网络参数$\theta$，设定一个最优二进制掩码(mask) $m^{\ast }$用于提取最优的子网络，并且要求子网络的参数小于主网络，具体来说可以描述为：
m t ∗ = min ⁡ m t ∈ { 0 , 1 } ∣ θ ∣ 1 n t ∑ i = 1 n t L ( f ( x i , t ; θ ⊙ m t ) , y i , t ) − C subject to  ∣ m t ∗ ∣ ≤ c m_t^*=\min_{m_t\in\{0,1\}^{|\theta|}}\frac{1}{n_t}\sum_{i=1}^{n_t}\mathcal{L}(f(x_{i,t};\theta \odot m_t),y_{i,t}) -C \\ \text{subject to}\ |m_t^*| \leq c mt∗​=mt​∈{0,1}∣θ∣min​nt​1​i=1∑nt​​L(f(xi,t​;θ⊙mt​),yi,t​)−Csubject to ∣mt∗​∣≤c
其中$C=\mathcal{L}(f(x_{i,t};\theta ),y_{i,t})$

2.1 Winning SubNetworks

假设可以给每一个网络权重$w$进行打分，分值越高代表该网路对任务的贡献越大，之后就可以进行评估（这里作者其实就是大概介绍了他们的思路以及为啥要用子网络，没有什么特别的信息，具体的方法在下面介绍）而实现子网络，具体的图如下：

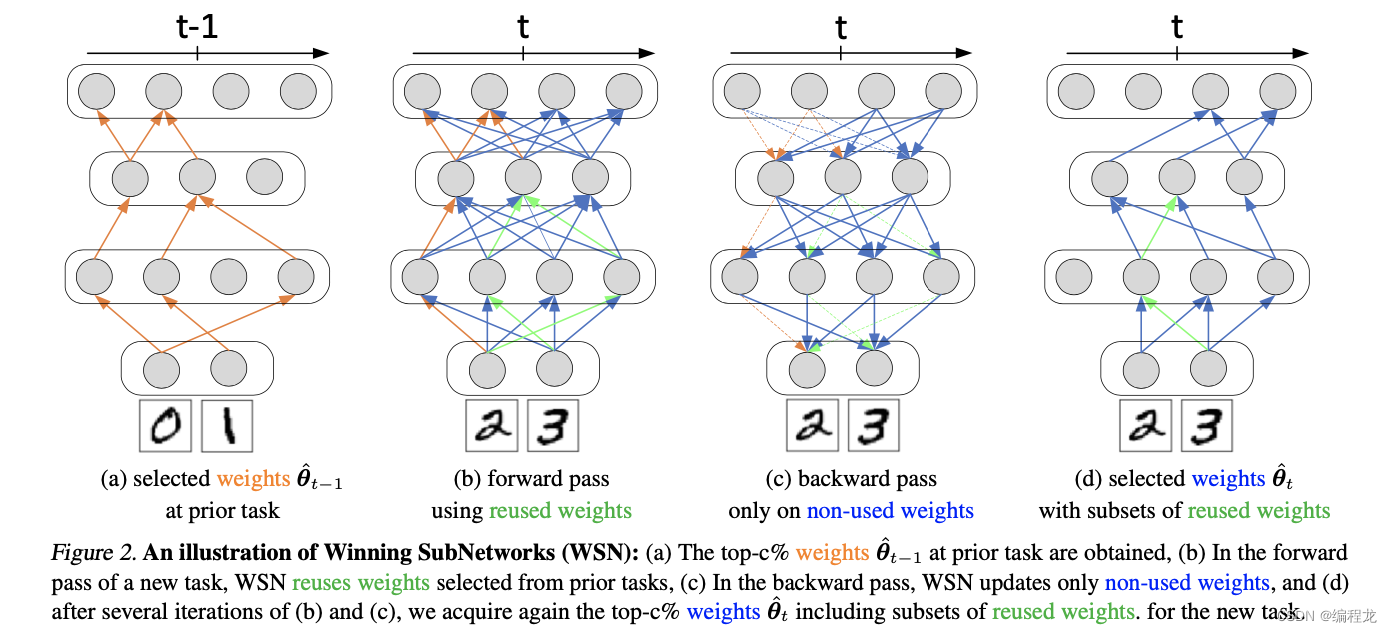
值得注意的是，新的任务也会用到之前任务学习过的参数，但为了不破坏之前的参数，因此不会选择去更新旧的参数。

2.2 具体的优化过程

有了子网络后，我们的优化目标变为：
$$\underset{\theta ,s}{\min }\mathcal{L}(\theta \odot m_t;{\mathcal{D}}_t)$$
此处$s$表示给每个权重的打分。然而，这种普通的优化过程存在两个问题：（1）在新任务的训练时更新所有$\theta$会干扰为以前任务分配的权重，（2）我们无法使用梯度更新分值$s$。为了解决第一个问题，这里使用选择性地更新参数。具体来说，假设$M_{t-1}={\vee }_{i=1}^{t-1}{m}_i$表示之前所有任务的掩码集合，那么更新变为：
$$\theta \leftarrow \theta -\eta (\frac{\partial \mathcal{L}}{\partial \theta }\odot (1-M_{t-1}))$$
这样就能保证冻结住那些已经被训练过的参数。对于第二个问题，可以使用top-c%进行分数的打分（这里到具体代码解释）。整体的算法如下：

2.3 掩码的编码过程

可以发现，上述需要存放掩码，这里作者使用每7位形成一个ASCII编码进行存储，减少存储量。（举个例子，假如现在掩码为0011000101000001010…，我们每7个进行存储，第一个就是0110000转换成十进制为42，对应于就是数字0），这样能大大减少空间。

三. 代码解析

作者的代码点这里。
上述两个关键的就是，实现子网络，这里代码为：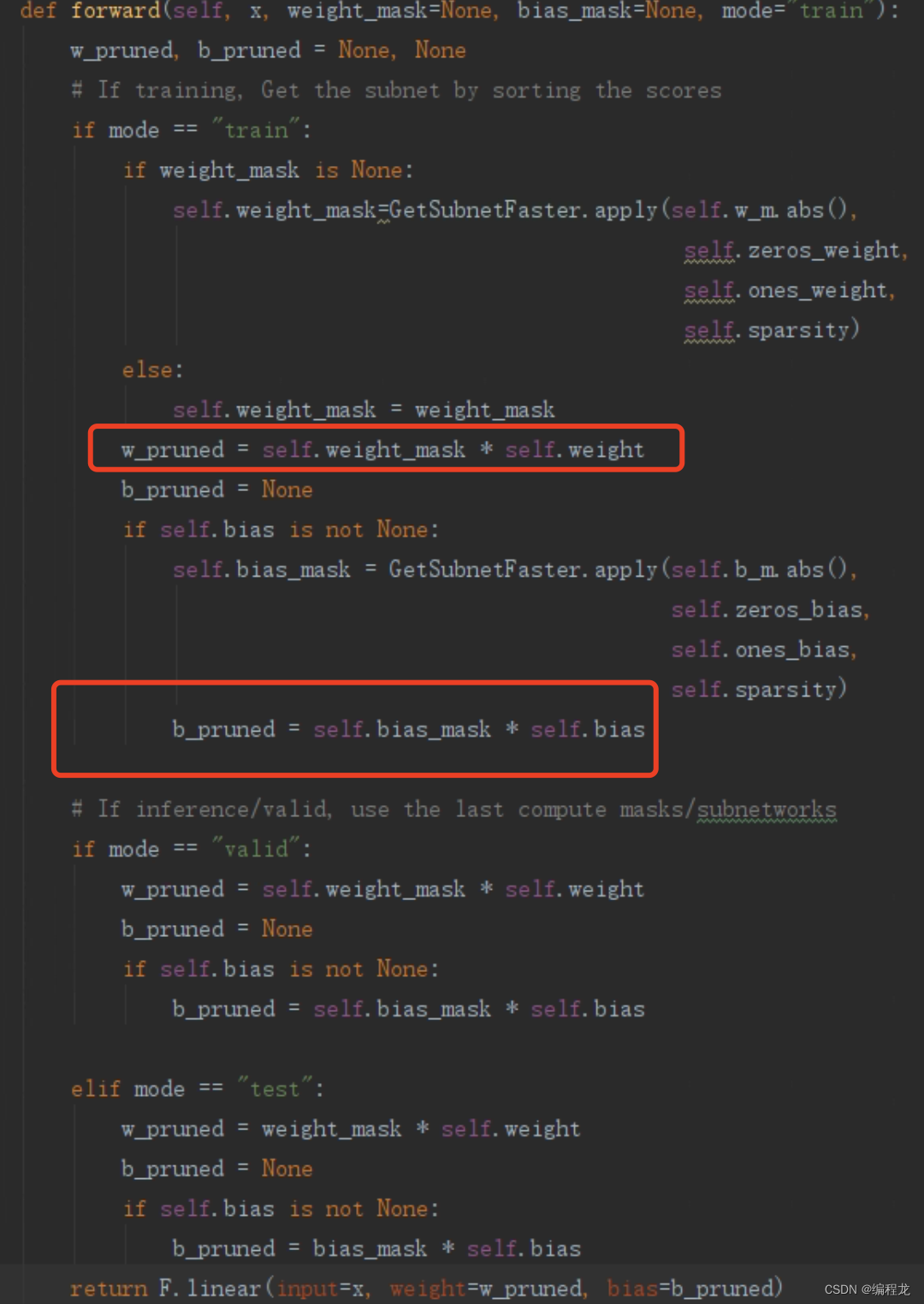

这里是作者重写了一个全连接层，红框标出的就是掩码和参数的过程，那么对于每一个网络掩码的是如何确定的呢？可以发现其对应于GetSubnetFaster里面，我们具体来看看：

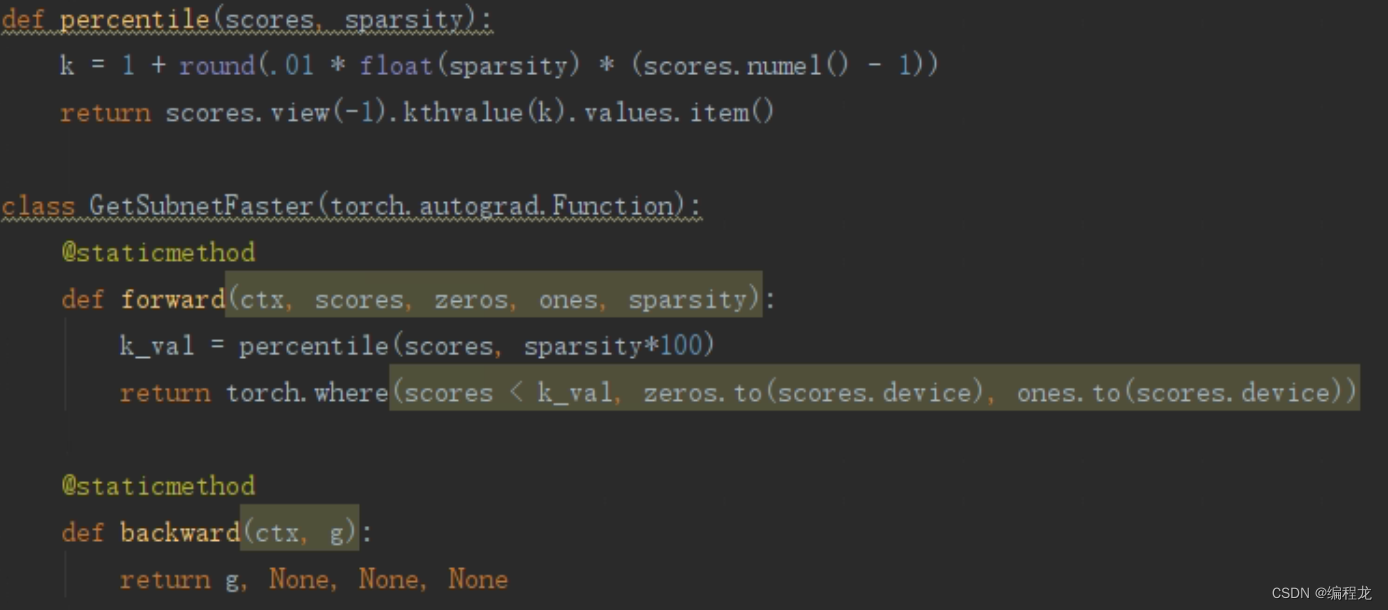
首先对应于forward来，这里scores对应的就是全连接层的参数$w$（这里要取绝对值），sparsity是一个提前定义好的量，表示为稀疏度，在0-1之间，在进行计算的时候，首先运行到percentile中，我们使用稀疏度*参数个数得到k，然后根据k计算网络中的第k_val大的数字（也就是求k分数），之后再将比k_val大的变为1其余变为0。因此，其实这里就是用了最标准的剪枝算法，选择前k个最大的权值，而剩余的舍弃。这里就是作者利用提到的分数的计算规则，而注意到backward，在计算梯度的时候是直接将传入的梯度g直接传出，而在一个任务训练多轮中，每一次都会变化参数而导致分位数变化从而实现掩码的变化。
第二个部分就简单了，那就是每次更新的参数只能是那些没有用过的，代码如下(train函数里面)：

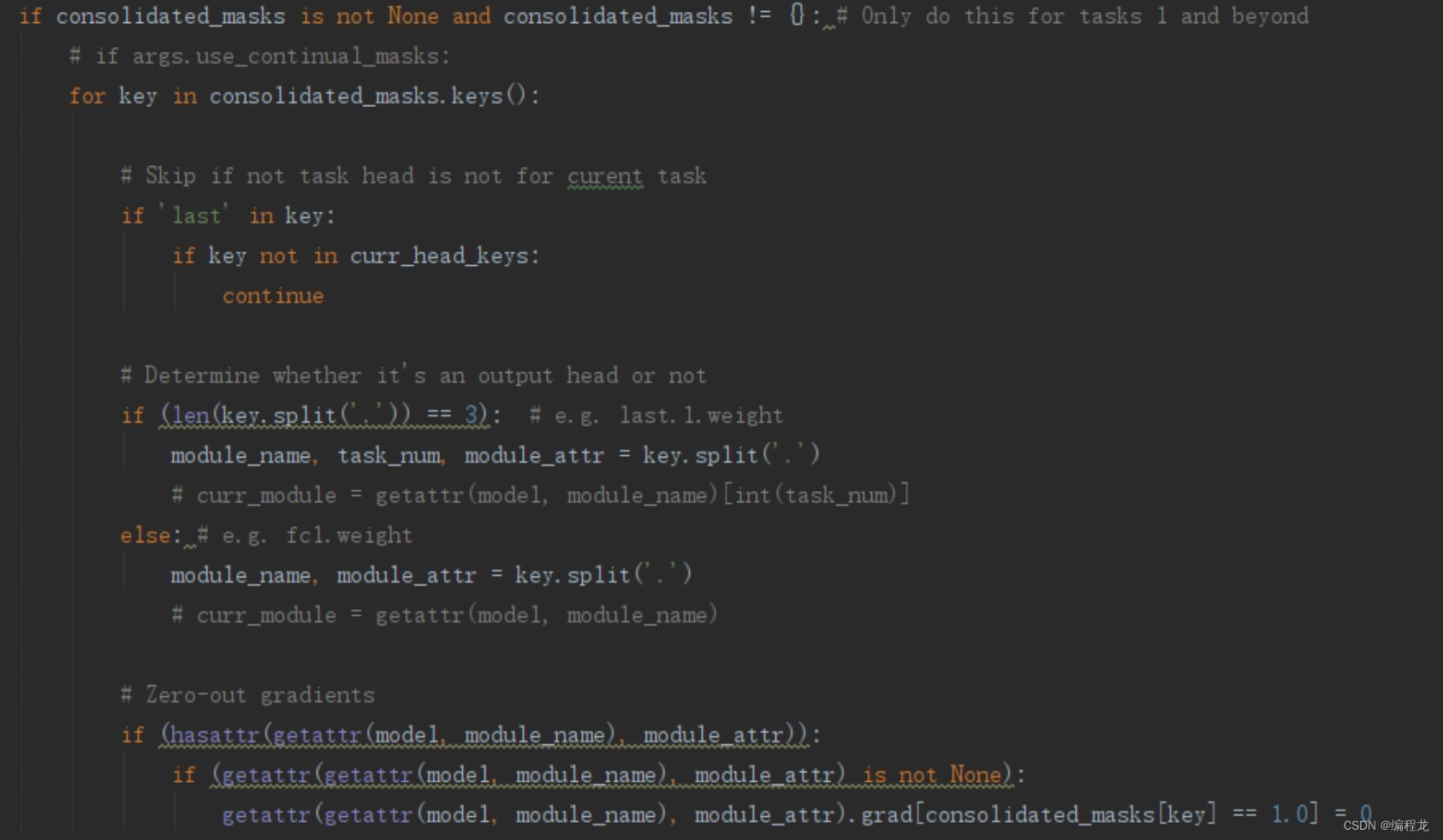
也就是依次找到那些被用过的参数，让他们的grad变为0即可。最后就是训练完一个任务后把他的掩码和之前的掩码合并：

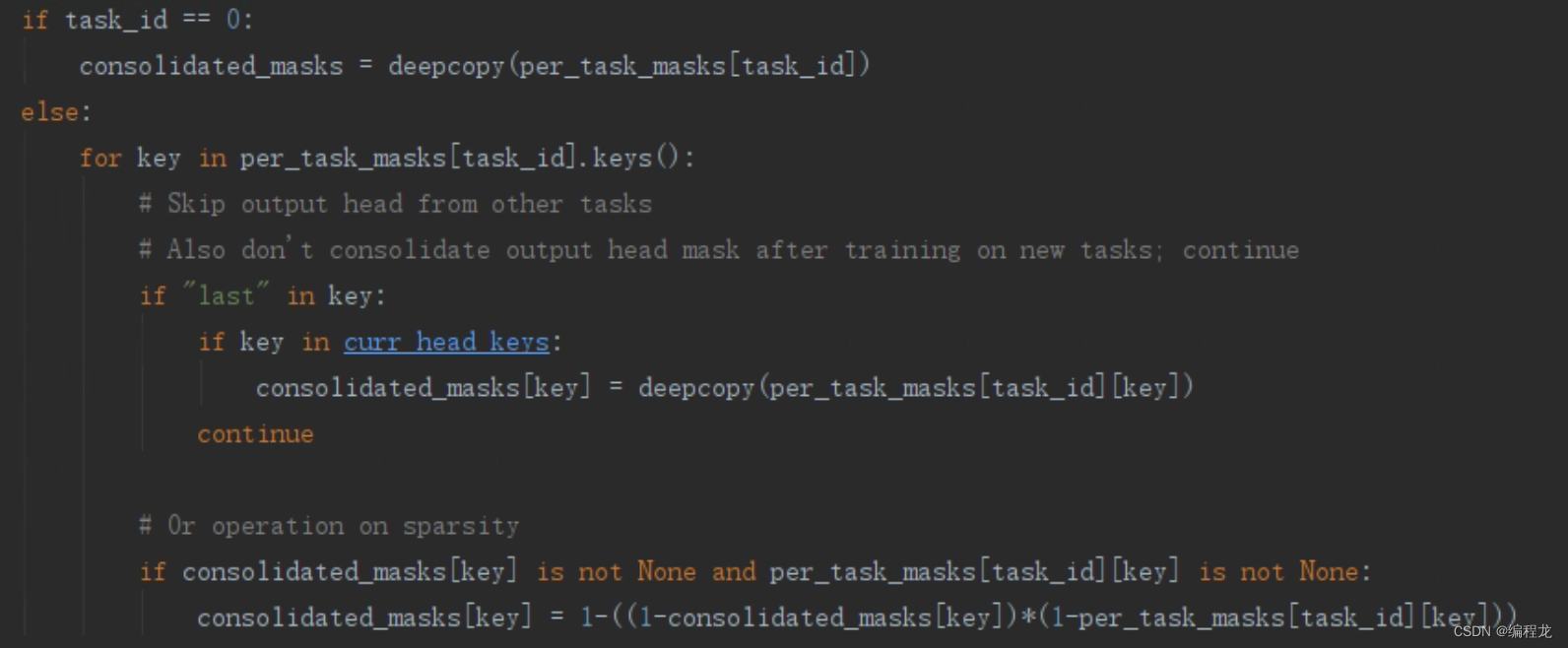
这次的论文想法还是挺行的，而且和FedWEIT一样都使用了掩码，欢迎大家提出意见～