本文主要是介绍《机器学习实战》学习记录-ch4,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
4.1 线性回归
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
X = 2 * np.random.rand(100,1) # 生成 [0,1) 之间的数据
y = 4 + 3 * X + np.random.randn(100,1) # 生成一组正态分布的数据, 高斯噪声
X_b = np.c_[np.ones((100,1)), X]
X_b[:5]
array([[1. , 0.74847244],[1. , 1.03567501],[1. , 0.92533857],[1. , 1.15770818],[1. , 0.46673679]])
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y) # 公式法求最小loss
theta_best
array([[4.07095749],[2.83726643]])
# 预测
X_new = np.array([[0], [2]])
X_new_b = np.c_[np.ones((2, 1)), X_new] # add x0 = 1 to each instance
y_predict = X_new_b.dot(theta_best)
y_predict
array([[4.07095749],[9.74549035]])
plt.plot(X_new, y_predict, "r-")
plt.plot(X, y, "b.")
plt.axis([-1, 3, 0, 15])
plt.show()

# 用 sklearn 的 LinearRegression
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X, y)
lin_reg.intercept_, lin_reg.coef_ # 截距 系数(array([4.07095749]), array([[2.83726643]]))
lin_reg.predict(X_new)
array([[4.07095749],[9.74549035]])
# LinearRegression 基于linalg.lstsq
theta_best_svd, residuals, rank, s = np.linalg.lstsq(X_b, y, rcond=1e-6)
theta_best_svd
array([[4.07095749],[2.83726643]])
4.2 梯度下降
通过测量参数向量θ相关的误差函数的局部梯度,并不断沿着降低梯度的方向调整,直到梯度降为0,到达最小值!(降低时间复杂度,不用求逆矩阵)
首先使用一个随机的θ值(这被称为随机初始化),然后逐步改进,每次踏出一步,每一步都尝试降低一点成本函数(如MSE),直到算法收敛出一个最小值
梯度下降中一个重要参数是每一步的步长,这取决于超参数学习率。如果学习率太低,算法需要经过大量迭代才能收敛。反过来说,如果学习率太高,那你可能会越过山谷直接到达另一边,甚至有可能比之前的起点还要高。
线性回归模型的MSE成本函数恰好是个凸函数,这意味着连接曲线上任意两点的线段永远不会跟曲线相交。也就是说,不存在局部最小值,只有一个全局最小值。它同时也是一个连续函数,所以斜率不会产生陡峭的变化[1]
成本函数虽然是碗状的,但如果不同特征的尺寸差别巨大,那它可能是一个非常细长的碗。如图4-7所示的梯度下降,左边的训练集上特征1和特征2具有相同的数值规模,而右边的训练集上,特征1的值则比特征2要小得多(注:因为特征1的值较小,所以θ1需要更大的变化来影响成本函数,这就是为什么碗形会沿着θ1轴拉长。)。
# (全)批量梯度下降
eta = 0.1 # learning rate
n_iterations = 1000
m = 100theta = np.random.randn(2,1) # random initializationfor iteration in range(n_iterations):gradients = 2/m * X_b.T.dot(X_b.dot(theta) - y)theta = theta - eta * gradients
theta
array([[4.07095749],[2.83726643]])
请注意,在计算梯度下降的每一步时,都是基于完整的训练集X的。这就是为什么该算法会被称为批量梯度下降:每一步都使用整批训练数据(实际上,全梯度下降可能是个更好的名字)。因此,面对非常庞大的训练集时,算法会变得极慢(不过我们即将看到快得多的梯度下降算法)。但是,梯度下降算法随特征数量扩展的表现比较好。如果要训练的线性模型拥有几十万个特征,
使用梯度下降比标准方程或者SVD要快得多。
4.2.2 随机梯度下降
批量梯度下降的主要问题是它要用整个训练集来计算每一步的梯度,所以训练集很大时,算法会特别慢。与之相反的极端是随机梯度下降,每一步在训练集中随机选择一个实例,并且仅基于该单个实例来计算梯度。显然,这让算法变得快多了,因为每次迭代都只需要操作少量的数据。它也可以被用来训练海量的数据集,因为每次迭代只需要在内存中运行一个实例即可(SGD可以作为核外算法实现,见第1章)。另一方面,由于算法的随机性质,它比批量梯度下降要不规则得多。成本函数将不再是缓缓降低直到抵达最小值,而是不断上上下下,但是从整体来看,还是在慢慢下降。随着时间的推移,最终会非常接近最小值,但是即使它到达了最小值,依旧还会持续反弹,永远不会停止(见图4-9)。所以算法停下来的参数值肯定是足够好的,但不是最优的。
- 好处:逃离局部最优;训练步骤块
- 坏处:得不到最优解。
解决方案:逐步降低学习率。
开始的步长比较大(这有助于快速进展和逃离局部最小值),然后越来越小,让算法尽量靠近全局最小值。这个过程叫作模拟退火,因为它类似于冶金时熔化的金属慢慢冷却的退火过程。
n_epochs = 50
t0, t1 = 5, 50 # learning schedule hyperparametersdef learning_schedule(t):return t0 / (t + t1)theta = np.random.randn(2,1) # random initializationfor epoch in range(n_epochs): # 退火温度for i in range(m): # 每个温度下取 m 次样本random_index = np.random.randint(m) # 随机选取一个样本xi = X_b[random_index:random_index+1]yi = y[random_index:random_index+1]gradients = 2 * xi.T.dot(xi.dot(theta) - yi)eta = learning_schedule(epoch * m + i)theta = theta - eta * gradients
theta
array([[4.06399722],[2.793174 ]])
要使用带有Scikit-Learn的随机梯度下降执行线性回归,可以使用SGDRegressor类,该类默认优化平方误差成本函数。以下代码最多可运行1000个轮次,或者直到一个轮次期间损失下降小于0.001为止(max_iter=1000,tol=1e-3)。它使用默认的学习调度(与前一个学习调度不同)以0.1(eta0=0.1)的学习率开始。最后,它不使用任何正则化(penalty=None,稍后将对此进行详细介绍):
# 调用 sklearn的 SGD
from sklearn.linear_model import SGDRegressor
sgd_reg = SGDRegressor(max_iter=1000, tol=1e-3, penalty=None, eta0=0.1)
sgd_reg.fit(X, y.ravel()) # ravel方法将y拉成一维数组
sgd_reg.intercept_, sgd_reg.coef_ # 截距,系数
(array([4.04727747]), array([2.84108153]))
4.2.3 小批量梯度下降
我们要研究的最后一个梯度下降算法称为小批量梯度下降。只要你了解了批量和随机梯度下降,就很容易理解它:在每一步中,不是根据完整的训练集(如批量梯度下降)或仅基于一个实例(如随机梯度下降)来计算梯度,小批量梯度下降在称为小型批量的随机实例集上计算梯度。小批量梯度下降优于随机梯度下降的主要优点是,你可以通过矩阵操作的硬件优化来提高性能,特别是在使用GPU时。
4.3 多项式回归
- 一元多项式
如果你的数据比直线更复杂怎么办?令人惊讶的是,你可以使用线性模型来拟合非线性数据。一个简单的方法就是将每个特征的幂次方添加为一个新特征,然后在此扩展特征集上训练一个线性模型。这种技术称为多项式回归。
# 生成一些非线性数据
m = 100
X = 6 * np.random.rand(m,1) - 3
y = 0.5 * X **2 + X + 2 + np.random.randn(m,1)
plt.plot(X,y,'b.')
[<matplotlib.lines.Line2D at 0x17cbe209580>]

from sklearn.preprocessing import PolynomialFeatures
poly_features = PolynomialFeatures(degree=2, include_bias=False)
X_poly = poly_features.fit_transform(X)
X[0]
array([-2.81222103])
X_poly[0]
array([-2.81222103, 7.90858713])
lin_reg = LinearRegression()
lin_reg.fit(X_poly, y)
lin_reg.intercept_, lin_reg.coef_
(array([1.85755943]), array([[1.04877191, 0.52580038]]))
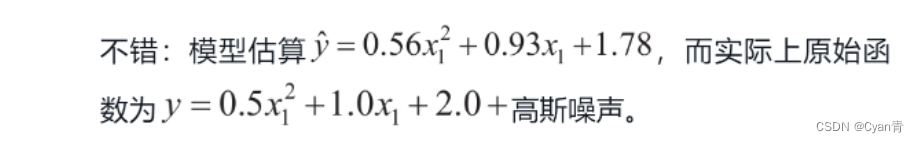
请注意,当存在多个特征时,多项式回归能够找到特征之间的关系(这是普通线性回归模型无法做到的)。PolynomialFeatures还可以将特征的所有组合添加到给定的多项式阶数。例如,如果有两个特征a和b,则degree=3的PolynomialFeatures不仅会添加特征a2、a3、b2和b3,还会添加组合ab、a2b和ab2。
https://blog.csdn.net/qq_45797116/article/details/112787290
4.4 学习曲线
高阶多项式回归可能会出现过拟合(交叉验证,泛化判定)
所以怎么确定多项式次数?-> 观察学习曲线
这个曲线绘制的是模型在训练集和验证集上关于训练集大小(或训练迭代)的性能函数。要生成这个曲线,只需要在不同大小的训练子集上多次训练模型即可。
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_splitdef plot_learning_curves(model, X, y):X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2)train_errors, val_errors = [], []for m in range(1, len(X_train)):model.fit(X_train[:m], y_train[:m])y_train_predict = model.predict(X_train[:m]) # 训练集预测y_val_predict = model.predict(X_val) # 验证集预测train_errors.append(mean_squared_error(y_train[:m], y_train_predict))val_errors.append(mean_squared_error(y_val, y_val_predict))plt.plot(np.sqrt(train_errors), "r-+", linewidth=2, label="train")plt.plot(np.sqrt(val_errors), "b-", linewidth=3, label="val")
lin_reg = LinearRegression()
plot_learning_curves(lin_reg, X, y)
plt.legend()
<matplotlib.legend.Legend at 0x17cbe29ebe0>

首先,让我们看一下在训练数据上的性能:当训练集中只有一个或两个实例时,模型可以很好地拟合它们,这就是曲线从零开始的原因。但是,随着将新实例添加到训练集中,模型就不可能完美地拟合训练数据,这既因为数据有噪声,又因为它根本不是线性的。因此,训练数据上的误差会一直上升,直到达到平稳状态,此时在训练集中添加新实例并不会使平均误差变好或变差。现在让我们看一下模型在验证数据上的性能。当在很少的训练实例上训练模型时,它无法正确泛化,这就是验证误差最初很大的原因。然后,随着模型经历更多的训练示例,它开始学习,因此验证错误逐渐降低。但是,直线不能很好地对数据进行建模,因此误差最终达到一个平稳的状态,非常接近另外一条曲线。这些学习曲线是典型的欠拟合模型。两条曲线都达到了平稳状态。它们很接近而且很高。
- 如果你的模型欠拟合训练数据,添加更多训练示例将无济于事。你需要使用更复杂的模型或提供更好的特征。
from sklearn.pipeline import Pipelinepolynomial_regression = Pipeline([("poly_features", PolynomialFeatures(degree=10, include_bias=False)),("lin_reg", LinearRegression()),])plot_learning_curves(polynomial_regression, X, y)
plt.legend()
<matplotlib.legend.Legend at 0x17cbead9550>

其实后面没有重合的,因为y变化太大被稀释了
- 改善过拟合模型的一种方法是向其提供更多的训练数据,直到验证误差达到训练误差为止。
模型的泛化误差
- 偏差:这部分泛化误差的原因在于错误的假设,比如假设数据是线性的,而实际上是二次的。高偏差模型最有可能欠拟合训练数据。
- 方差:这部分是由于模型对训练数据的细微变化过于敏感。具有许多自由度的模型(例如高阶多项式模型)可能具有较高的方差,因此可能过拟合训练数据。
- 不可避免的误差。(数据本身的噪声)
4.5 正则化线性模型
减少过拟合的一个好方法是对模型进行正则化(即约束模型):它拥有的自由度越少,则过拟合数据的难度就越大。正则化多项式模型的一种简单方法是减少多项式的次数。对于线性模型,正则化通常是通过约束模型的权重来实现的。
4.5.1 岭回归
岭回归(也称为Tikhonov正则化)是线性回归的正则化版本
超参数α控制要对模型进行正则化的程度。如果α=0,则岭回归仅是线性回归。如果α非常大,则所有权重最终都非常接近于零,结果是一条经过数据均值的平线
在执行岭回归之前缩放数据(例如使用StandardScaler)很重要,因为它对输入特征的缩放敏感。大多数正则化模型都需要如此。
请注意,α的增加会导致更平坦(即不极端,更合理)的预测,从而减少了模型的方差,但增加了其偏差。(alpha越大,惩罚越大,斜率(权重)不会高)
from sklearn.linear_model import Ridge
ridge_reg = Ridge(alpha=1, solver="cholesky")
ridge_reg.fit(X, y)
ridge_reg.predict([[1.5]])
array([[5.250856]])
# 12 范数 梯度下降
sgd_reg = SGDRegressor(penalty="l2")
sgd_reg.fit(X, y.ravel())
sgd_reg.predict([[1.5]])
array([5.22860513])
4.5.2 Lasso回归
线性回归的另一种正则化叫作最小绝对收缩和选择算子回归,与岭回归一样,它也是向成本函数添加一个正则项,但是它增加的是权重向量的L1范数
。换句话说,Lasso回归会自动执行特征选择并输出一个稀疏模型(即只有很少的特征有非零权重)。
4.5.3 弹性网络
弹性网络是介于岭回归和Lasso回归之间的中间地带。正则项是岭和Lasso正则项的简单混合,你可以控制混合比r。当r=0时,弹性网络等效于岭回归,而当r=1时,弹性网络等效于Lasso回归。
4.5.4 提前停止
使用随机和小批量梯度下降时,曲线不是那么平滑,可能很难知道你是否达到了最小值。一种解决方案是仅在验证错误超过最小值一段时间后停止(当你确信模型不会做得更好时),然后回滚模型参数到验证误差最小的位置。
from sklearn.base import clone# prepare the data
poly_scaler = Pipeline([("poly_features", PolynomialFeatures(degree=90, include_bias=False)),("std_scaler", StandardScaler())])
X_train_poly_scaled = poly_scaler.fit_transform(X_train)
X_val_poly_scaled = poly_scaler.transform(X_val)sgd_reg = SGDRegressor(max_iter=1, tol=-np.infty, warm_start=True,penalty=None, learning_rate="constant", eta0=0.0005)minimum_val_error = float("inf")
best_epoch = None
best_model = None
for epoch in range(1000):sgd_reg.fit(X_train_poly_scaled, y_train) # continues where it left offy_val_predict = sgd_reg.predict(X_val_poly_scaled)val_error = mean_squared_error(y_val, y_val_predict)if val_error < minimum_val_error:minimum_val_error = val_errorbest_epoch = epochbest_model = clone(sgd_reg)
这篇关于《机器学习实战》学习记录-ch4的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









