有数据结构的光学系统基点位置和焦距计算MATLAB程序

天大《工光》综合练习一，给出有数据结构的光学系统，求系统基点位置和焦距。

以如下光学系统为例：

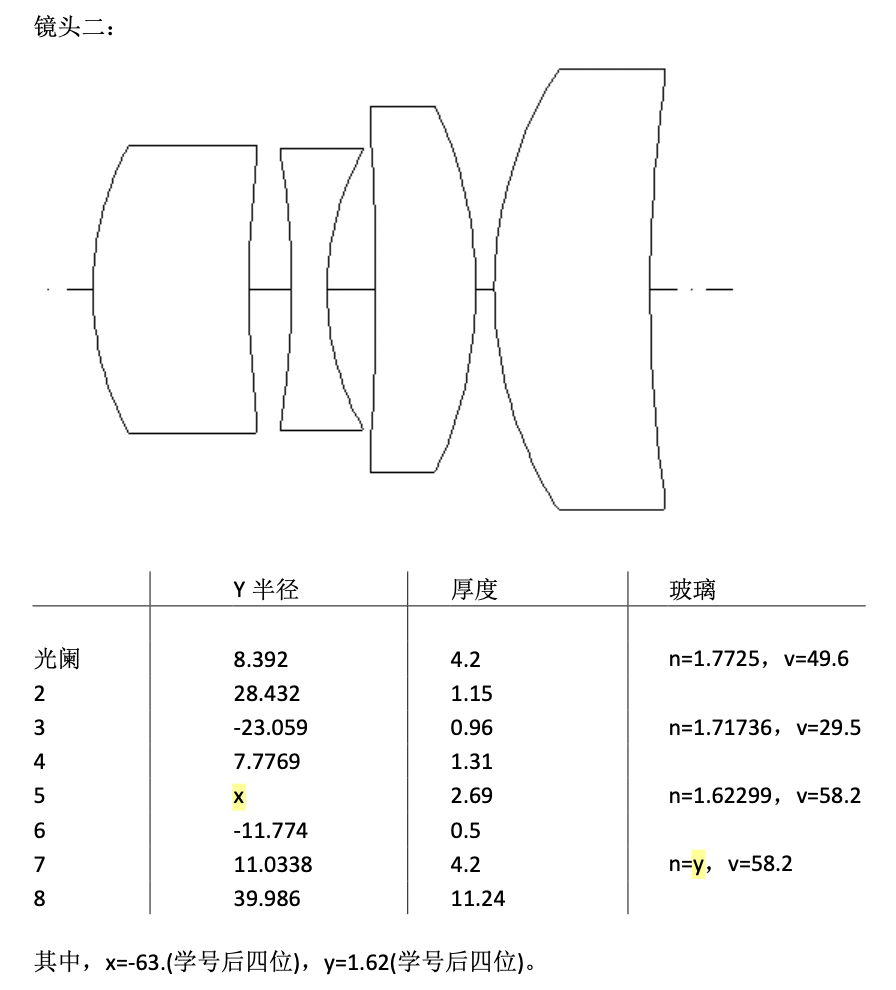
要求按表格完成计算过程（如下表格）：

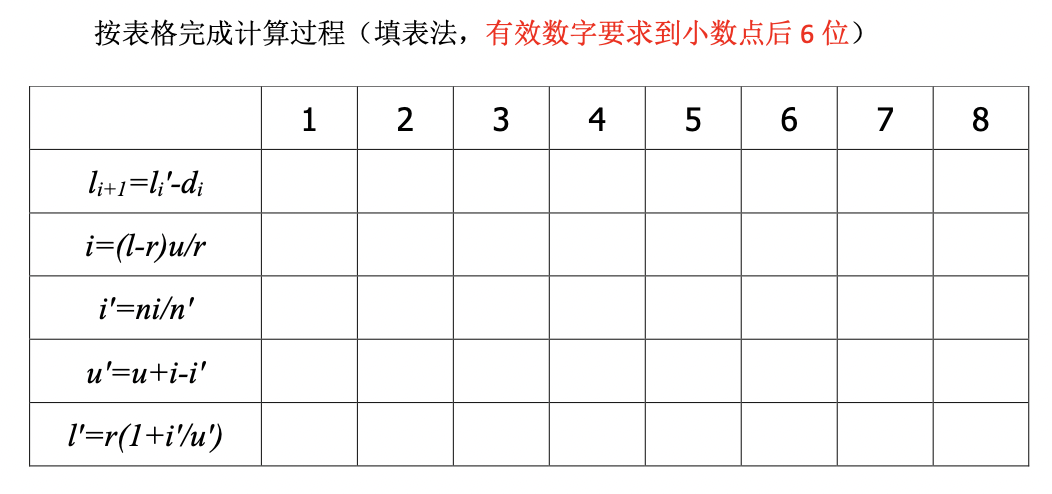
对于正向近轴光线光路计算，设计MATLAB代码如下：

clc
clear
r=[8.392,28.432,-23.059,7.7769,-63.2117,-11.774,11.0338,39.986];
d=[4.2,1.15,0.96,1.31,2.69,0.5,4.2,11.24];
n=[1.7725,1.71736,1.62299,1.622117];
n0=1;x=1;
while x<=8temp=1; u=0;i=1/r(1);while temp<=8if x<=2i2=i*(n(1)/n0)^((-1)^x);elseif (2<x)&&(x<=4)i2=i*(n(2)/n0)^((-1)^x);elseif (4<x)&&(x<=6)i2=i*(n(3)/n0)^((-1)^x);elsei2=i*(n(4)/n0)^((-1)^x);endu2=u+i-i2;l2=r(temp)*(1+(i2/u2));li=l2-d(temp);temp=temp+1;fprintf('i=%.8f \n',i);fprintf('i2=%.8f \n',i2);fprintf('u2=%.8f \n',u2);fprintf('l2=%.8f \n',l2);fprintf('li=%.8f \n',li);u=u2;if temp<=8i=(li-r(temp))*u/r(temp);endx=x+1;endend

其中i2为表格中i'；u2为表格中u'；l2为表格中l'；li为表格中li+1，由于l9没有存在可能，故输出程序最后一行无用。因表格要求保留小数点后六位，故在这里取后八位，可自行调整。

对于反向近轴光线光路计算，设计MATLAB代码如下：

clc
clear
r=[-39.986,-11.0338,11.774,63.2117,-7.7769,23.059,-28.432,-8.392];
d=[4.2,0.5,2.69,1.31,0.96,1.15,4.2,11.24];
n=[1.622117,1.62299,1.71736,1.7725];
n0=1;x=1;
while x<=8temp=1; u=0;i=1/r(1);while temp<=8if x<=2i2=i*(n(1)/n0)^((-1)^x);elseif (2<x)&&(x<=4)i2=i*(n(2)/n0)^((-1)^x);elseif (4<x)&&(x<=6)i2=i*(n(3)/n0)^((-1)^x);elsei2=i*(n(4)/n0)^((-1)^x);endu2=u+i-i2;l2=r(temp)*(1+(i2/u2));li=l2-d(temp);temp=temp+1;fprintf('i=%.8f \n',i);fprintf('i2=%.8f \n',i2);fprintf('u2=%.8f \n',u2);fprintf('l2=%.8f \n',l2);fprintf('li=%.8f \n',li);u=u2;if temp<=8i=(li-r(temp))*u/r(temp);endx=x+1;endend

容易理解，上面两个代码块很相似，仅仅是取反取负。