本文主要是介绍大菜鸡的计算几何之旅-[kuangbin带你飞]专题十三 基础计算几何,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
大菜鸡的计算几何之旅-[kuangbin带你飞]专题十三 基础计算几何
A POJ 2318 TOYS
Description
Calculate the number of toys that land in each bin of a partitioned toy box.
Mom and dad have a problem - their child John never puts his toys away when he is finished playing with them. They gave John a rectangular box to put his toys in, but John is rebellious and obeys his parents by simply throwing his toys into the box. All the toys get mixed up, and it is impossible for John to find his favorite toys.
John’s parents came up with the following idea. They put cardboard partitions into the box. Even if John keeps throwing his toys into the box, at least toys that get thrown into different bins stay separated. The following diagram shows a top view of an example toy box.

For this problem, you are asked to determine how many toys fall into each partition as John throws them into the toy box.
Input
The input file contains one or more problems. The first line of a problem consists of six integers, n m x1 y1 x2 y2. The number of cardboard partitions is n (0 < n <= 5000) and the number of toys is m (0 < m <= 5000). The coordinates of the upper-left corner and the lower-right corner of the box are (x1,y1) and (x2,y2), respectively. The following n lines contain two integers per line, Ui Li, indicating that the ends of the i-th cardboard partition is at the coordinates (Ui,y1) and (Li,y2). You may assume that the cardboard partitions do not intersect each other and that they are specified in sorted order from left to right. The next m lines contain two integers per line, Xj Yj specifying where the j-th toy has landed in the box. The order of the toy locations is random. You may assume that no toy will land exactly on a cardboard partition or outside the boundary of the box. The input is terminated by a line consisting of a single 0.
Output
The output for each problem will be one line for each separate bin in the toy box. For each bin, print its bin number, followed by a colon and one space, followed by the number of toys thrown into that bin. Bins are numbered from 0 (the leftmost bin) to n (the rightmost bin). Separate the output of different problems by a single blank line.
Sample Input
5 6 0 10 60 0
3 1
4 3
6 8
10 10
15 30
1 5
2 1
2 8
5 5
40 10
7 9
4 10 0 10 100 0
20 20
40 40
60 60
80 80
5 10
15 10
25 10
35 10
45 10
55 10
65 10
75 10
85 10
95 10
0
Sample Output
0: 2
1: 1
2: 1
3: 1
4: 0
5: 1
0: 2
1: 2
2: 2
3: 2
4: 2
Hint
As the example illustrates, toys that fall on the boundary of the box are “in” the box.
题意
有一个长条形的盒子,盒子里面有一些隔板,往盒子里面丢一些东西,问每个小格子里面有多少东西。
思路
二分+叉积。
叉积为负表示在隔板的左边,否则在隔板的左边。
坑点
无。
本来还以为会炸LL,然鹅并没有,一发过。
代码
#include <cstdio>
#include <iostream>using namespace std;typedef long long ll;#define rep(i,a,b) for(int i=a;i<=b;i++)
#define per(i,a,b) for(int i=a;i>=b;i--)const int N=5005;int n,m,x1,y1,x2,y2;struct S
{int top,low,num;
} board[N];int vp(int xx1,int yy1,int xx2,int yy2,int xx3,int yy3)
{return -xx1*yy2+xx1*yy3+xx2*yy1-xx2*yy3-xx3*yy1+xx3*yy2;
}void cal(int x,int y)
{int l=1,r=n;int ans=1;while(l<r){int mid=(l+r)/2;if(vp(x,y,board[mid].top,y1,board[mid].low,y2)<0){l=mid+1;ans=l;}else{r=mid;}}board[ans].num++;
}int main()
{int flag=0;while(~scanf("%d",&n)&&n){scanf("%d%d%d%d%d",&m,&x1,&y1,&x2,&y2);rep(i,1,n){scanf("%d%d",&board[i].top,&board[i].low);board[i].num=0;}n++;board[n].top=y1;board[n].low=y2;board[n].num=0;rep(i,1,m){int x,y;scanf("%d%d",&x,&y);cal(x,y);}if(flag)printf("\n");flag=1;rep(i,1,n){printf("%d: %d\n",i-1,board[i].num);}}return 0;
}B POJ 2398 Toy Storage
Description
Mom and dad have a problem: their child, Reza, never puts his toys away when he is finished playing with them. They gave Reza a rectangular box to put his toys in. Unfortunately, Reza is rebellious and obeys his parents by simply throwing his toys into the box. All the toys get mixed up, and it is impossible for Reza to find his favorite toys anymore.
Reza’s parents came up with the following idea. They put cardboard partitions into the box. Even if Reza keeps throwing his toys into the box, at least toys that get thrown into different partitions stay separate. The box looks like this from the top:

We want for each positive integer t, such that there exists a partition with t toys, determine how many partitions have t, toys.
Input
The input consists of a number of cases. The first line consists of six integers n, m, x1, y1, x2, y2. The number of cardboards to form the partitions is n (0 < n <= 1000) and the number of toys is given in m (0 < m <= 1000). The coordinates of the upper-left corner and the lower-right corner of the box are (x1, y1) and (x2, y2), respectively. The following n lines each consists of two integers Ui Li, indicating that the ends of the ith cardboard is at the coordinates (Ui, y1) and (Li, y2). You may assume that the cardboards do not intersect with each other. The next m lines each consists of two integers Xi Yi specifying where the ith toy has landed in the box. You may assume that no toy will land on a cardboard.
A line consisting of a single 0 terminates the input.
Output
For each box, first provide a header stating “Box” on a line of its own. After that, there will be one line of output per count (t > 0) of toys in a partition. The value t will be followed by a colon and a space, followed the number of partitions containing t toys. Output will be sorted in ascending order of t for each box.
Sample Input
4 10 0 10 100 0
20 20
80 80
60 60
40 40
5 10
15 10
95 10
25 10
65 10
75 10
35 10
45 10
55 10
85 10
5 6 0 10 60 0
4 3
15 30
3 1
6 8
10 10
2 1
2 8
1 5
5 5
40 10
7 9
0
Sample Output
Box
2: 5
Box
1: 4
2: 1
题意
有一个长条形的盒子,盒子里面有一些隔板,往盒子里面丢一些东西,问小格子里有某个物品的格子数是多少。
思路
跟A题几乎一样。稍微改了一点点。
坑点
无
代码
#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;typedef long long ll;#define rep(i,a,b) for(int i=a;i<=b;i++)
#define per(i,a,b) for(int i=a;i>=b;i--)const int N=5005;int n,m,x1,y1,x2,y2;struct S
{int top,low,num;
} board[N];struct SS
{int num;int sum;
} _ans[1005];void init()
{rep(i,0,1004){_ans[i].sum=0;_ans[i].num=i;}
}bool cmp(S aa,S bb)
{return aa.top<bb.top;
}int vp(int xx1,int yy1,int xx2,int yy2,int xx3,int yy3)
{return -xx1*yy2+xx1*yy3+xx2*yy1-xx2*yy3-xx3*yy1+xx3*yy2;
}void cal(int x,int y)
{int l=1,r=n;int ans=1;while(l<r){int mid=(l+r)/2;
// cout<<vp(x,y,board[mid].top,y1,board[mid].low,y2)<<endl;
// cout<<"debug:"<<board[mid].top<<endl;if(vp(x,y,board[mid].top,y1,board[mid].low,y2)<0){l=mid+1;ans=l;}else{r=mid;}}_ans[board[ans].num].sum--;board[ans].num++;_ans[board[ans].num].sum++;
}int main()
{while(~scanf("%d",&n)){if(n==0)break;init();scanf("%d%d%d%d%d",&m,&x1,&y1,&x2,&y2);rep(i,1,n){scanf("%d%d",&board[i].top,&board[i].low);board[i].num=0;}sort(board+1,board+1+n,cmp);n++;board[n].top=y1;board[n].low=y2;board[n].num=0;rep(i,1,m){int x,y;scanf("%d%d",&x,&y);cal(x,y);}printf("Box\n");rep(i,1,m){if(_ans[i].sum==0)continue;printf("%d: %d\n",_ans[i].num,_ans[i].sum);}}return 0;
}C POJ 3304 Segments
Description
Given n segments in the two dimensional space, write a program, which determines if there exists a line such that after projecting these segments on it, all projected segments have at least one point in common.
Input
Input begins with a number T showing the number of test cases and then, T test cases follow. Each test case begins with a line containing a positive integer n ≤ 100 showing the number of segments. After that, n lines containing four real numbers x1 y1 x2 y2 follow, in which (x1, y1) and (x2, y2) are the coordinates of the two endpoints for one of the segments.
Output
For each test case, your program must output “Yes!”, if a line with desired property exists and must output “No!” otherwise. You must assume that two floating point numbers a and b are equal if |a - b| < 10-8.
Sample Input
3
2
1.0 2.0 3.0 4.0
4.0 5.0 6.0 7.0
3
0.0 0.0 0.0 1.0
0.0 1.0 0.0 2.0
1.0 1.0 2.0 1.0
3
0.0 0.0 0.0 1.0
0.0 2.0 0.0 3.0
1.0 1.0 2.0 1.0
Sample Output
Yes!
Yes!
No!
题意
给定n条线段,问能否找到一条直线使得所有线段在直线上的投影至少有一个交点。
思路
如果存在一条这样的直线,那么过投影相交区域作直线的垂线,该垂线必定与每条线段相交,问题转化为问是否存在一条线和所有线段相交。
遍历所有线段的两个端点构成的直线,判断是否满足条件即可。
坑点
需要考虑EPS,如果两点间的距离小于EPS(1e-8),则视为同一个点。
代码
#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>using namespace std;typedef long long ll;#define rep(i,a,b) for(int i=a;i<=b;i++)
#define per(i,a,b) for(int i=a;i>=b;i--)const int N=110;
const double EPS=1e-8;int n;struct P
{double x,y;
};struct L
{P p1,p2;
} lin[N];double distan(double x1,double y1,double x2,double y2)
{return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
}double cj(double x1,double y1,double x2,double y2,double x3,double y3)
{return (x3-x2)*(y1-y2)-(x1-x2)*(y3-y2);
}bool cross(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4)
{
// bool ans=min(x1,x2)<=max(x3,x4)&&min(x3,x4)<=max(x1,x2)&&min(y1,y2)<=max(y3,y4)&&min(y3,y4)<=max(y1,y2);
// if(!ans) return false;bool ans;if(cj(x1,y1,x2,y2,x3,y3)*cj(x1,y1,x2,y2,x4,y4)>EPS)ans=false;elseans=true;return ans;
}bool cal(double x1,double y1,double x2,double y2)
{if(distan(x1,y1,x2,y2)<EPS)return false;bool ans=true;rep(i,1,n){if(cross(x1,y1,x2,y2,lin[i].p1.x,lin[i].p1.y,lin[i].p2.x,lin[i].p2.y)==false){ans=false;break;}}return ans;
}int main()
{int T;scanf("%d",&T);while(T--){scanf("%d",&n);rep(i,1,n){scanf("%lf%lf%lf%lf",&lin[i].p1.x,&lin[i].p1.y,&lin[i].p2.x,&lin[i].p2.y);}if(n==1){printf("Yes!\n");continue;}bool ans=false;rep(i,1,n){rep(j,i+1,n){if(cal(lin[i].p1.x,lin[i].p1.y,lin[j].p1.x,lin[j].p1.y)==true||cal(lin[i].p1.x,lin[i].p1.y,lin[j].p2.x,lin[j].p2.y)==true||cal(lin[i].p2.x,lin[i].p2.y,lin[j].p1.x,lin[j].p1.y)==true||cal(lin[i].p2.x,lin[i].p2.y,lin[j].p2.x,lin[j].p2.y)==true){ans=true;break;}}if(ans==true)break;}if(ans)printf("Yes!\n");elseprintf("No!\n");}return 0;
}D POJ 1269 Intersecting Lines
Description
We all know that a pair of distinct points on a plane defines a line and that a pair of lines on a plane will intersect in one of three ways: 1) no intersection because they are parallel, 2) intersect in a line because they are on top of one another (i.e. they are the same line), 3) intersect in a point. In this problem you will use your algebraic knowledge to create a program that determines how and where two lines intersect.
Your program will repeatedly read in four points that define two lines in the x-y plane and determine how and where the lines intersect. All numbers required by this problem will be reasonable, say between -1000 and 1000.
Input
The first line contains an integer N between 1 and 10 describing how many pairs of lines are represented. The next N lines will each contain eight integers. These integers represent the coordinates of four points on the plane in the order x1y1x2y2x3y3x4y4. Thus each of these input lines represents two lines on the plane: the line through (x1,y1) and (x2,y2) and the line through (x3,y3) and (x4,y4). The point (x1,y1) is always distinct from (x2,y2). Likewise with (x3,y3) and (x4,y4).
Output
There should be N+2 lines of output. The first line of output should read INTERSECTING LINES OUTPUT. There will then be one line of output for each pair of planar lines represented by a line of input, describing how the lines intersect: none, line, or point. If the intersection is a point then your program should output the x and y coordinates of the point, correct to two decimal places. The final line of output should read “END OF OUTPUT”.
Sample Input
5
0 0 4 4 0 4 4 0
5 0 7 6 1 0 2 3
5 0 7 6 3 -6 4 -3
2 0 2 27 1 5 18 5
0 3 4 0 1 2 2 5
Sample Output
INTERSECTING LINES OUTPUT
POINT 2.00 2.00
NONE
LINE
POINT 2.00 5.00
POINT 1.07 2.20
END OF OUTPUT
题意
给定两条用两点表示的直线,问这两条直线是平行 重合 还是相交,如果是相交输出交点。
思路
由于题中要求的精度并不高,直接搞就行了。
坑点
无
代码
#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>using namespace std;typedef long long ll;#define rep(i,a,b) for(int i=a;i<=b;i++)
#define per(i,a,b) for(int i=a;i>=b;i--)const int N=110;
const double EPS=1e-8;int n;double cross(double x1,double y1,double x2,double y2,double x3,double y3)
{return (-x1*y2+x1*y3+x2*y1-x2*y3-x3*y1+x3*y2);
}bool intersect_line(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4)
{bool ans;if(cross(x1,y1,x2,y2,x3,y3)*cross(x1,y1,x2,y2,x4,y4)>EPS)ans=false;elseans=true;return ans;
}bool intersect_seg(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4)
{//快速排斥实验bool ans=min(x1,x2)<=max(x3,x4)&&min(x3,x4)<=max(x1,x2)&&min(y1,y2)<=max(y3,y4)&&min(y3,y4)<=max(y1,y2);if(!ans) return false;//快速跨立实验if(cross(x1,y1,x2,y2,x3,y3)*cross(x1,y1,x2,y2,x4,y4)>EPS)ans=false;elseans=true;return ans;
}int main()
{scanf("%d",&n);printf("INTERSECTING LINES OUTPUT\n");rep(cas,1,n){double x1,y1,x2,y2,x3,y3,x4,y4;scanf("%lf%lf%lf%lf%lf%lf%lf%lf",&x1,&y1,&x2,&y2,&x3,&y3,&x4,&y4);if((y2-y1)*(x4-x3)-(y4-y3)*(x2-x1)>-EPS&&(y2-y1)*(x4-x3)-(y4-y3)*(x2-x1)<EPS){if(cross(x1,y1,x2,y2,x3,y3)*cross(x1,y1,x2,y2,x4,y4)>-EPS&&cross(x1,y1,x2,y2,x3,y3)*cross(x1,y1,x2,y2,x4,y4)<EPS){printf("LINE\n");}else{printf("NONE\n");}}else{double ans_x=((x2-x1)*(y4-y3)*x3-(y2-y1)*(x4-x3)*x1+(y1-y3)*(x4-x3)*(x2-x1))/((y4-y3)*(x2-x1)-(y2-y1)*(x4-x3));double ans_y;if(!(x2-x1>=-EPS&&x2-x1<=EPS))ans_y=((y2-y1)/(x2-x1))*(ans_x-x1)+y1;elseans_y=((y4-y3)/(x4-x3))*(ans_x-x3)+y3;printf("POINT %.2f %.2f\n",ans_x,ans_y);}}printf("END OF OUTPUT\n");return 0;
}E POJ 1556 The Doors
Description
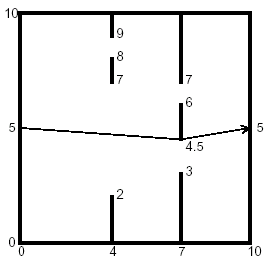
You are to find the length of the shortest path through a chamber containing obstructing walls. The chamber will always have sides at x = 0, x = 10, y = 0, and y = 10. The initial and final points of the path are always (0, 5) and (10, 5). There will also be from 0 to 18 vertical walls inside the chamber, each with two doorways. The figure below illustrates such a chamber and also shows the path of minimal length.
Input
The input data for the illustrated chamber would appear as follows.
2
4 2 7 8 9
7 3 4.5 6 7
The first line contains the number of interior walls. Then there is a line for each such wall, containing five real numbers. The first number is the x coordinate of the wall (0 < x < 10), and the remaining four are the y coordinates of the ends of the doorways in that wall. The x coordinates of the walls are in increasing order, and within each line the y coordinates are in increasing order. The input file will contain at least one such set of data. The end of the data comes when the number of walls is -1.
Output
The output should contain one line of output for each chamber. The line should contain the minimal path length rounded to two decimal places past the decimal point, and always showing the two decimal places past the decimal point. The line should contain no blanks.
Sample Input
1
5 4 6 7 8
2
4 2 7 8 9
7 3 4.5 6 7
-1
Sample Output
10.00
10.06
题意
给定一个10*10的房间,里面有一些墙,问从(0,5)走到(10,5)的最短的路径长度。
思路
遍历所有端点,用叉积判断这两点的连线会不会穿过墙,如果不会,记录i->j,j->i的距离为两点的直线距离,建边。然后跑最短路。
坑点
我要是再用%lf输出double类型,我就不玩了!
坑死我自己了。。。
我是演员。。。
代码
#include <iostream>
#include <cstdio>
#include <cmath>using namespace std;const int N=1005;
const double EPS=1e-8;typedef long long ll;#define rep(i,a,b) for(int i=a;i<=b;i++)
#define per(i,a,b) for(int i=a;i>=b;i--)int n;
double len[N][N];
int cntp,cntl;struct P
{double x,y;
} poi[N];struct L
{P p,q;
} lin[50];void __bug_len()
{rep(i,1,cntp){rep(j,1,cntp){printf("%10.5f",len[i][j]);}cout<<endl;}
}void init()
{rep(i,0,N-2){rep(j,0,N-2){len[i][j]=1000;}}cntp=0;cntl=0;
}double cross(double x1,double y1,double x2,double y2,double x3,double y3)
{return (-x1*y2+x1*y3+x2*y1-x2*y3-x3*y1+x3*y2);
}bool intersect_seg(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4)
{//快速排斥实验bool ans=min(x1,x2)<=max(x3,x4)&&min(x3,x4)<=max(x1,x2)&&min(y1,y2)<=max(y3,y4)&&min(y3,y4)<=max(y1,y2);if(!ans)return false;//快速跨立实验if(cross(x1,y1,x2,y2,x3,y3)*cross(x1,y1,x2,y2,x4,y4)>EPS)ans=false;elseans=true;return ans;
}bool judge(double x1,double y1,double x2,double y2)
{bool ans=true;rep(i,1,cntl){if(x1==lin[i].p.x||x2==lin[i].q.x)continue;if(intersect_seg(x1,y1,x2,y2,lin[i].p.x,lin[i].p.y,lin[i].q.x,lin[i].q.y)==true){ans=false;break;}}return ans;
}double distan(double x1,double y1,double x2,double y2)
{return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
}double cal()
{rep(i,1,cntp){rep(j,i+1,cntp){if(judge(poi[i].x,poi[i].y,poi[j].x,poi[j].y)){len[i][j]=distan(poi[i].x,poi[i].y,poi[j].x,poi[j].y);
// cout<<"DEBUGLEN:"<<i<<' '<<j<<' '<<len[i][j]<<endl;
// cout<<"DEBUGPOI:"<<poi[i].x<<' '<<poi[i].y<<' '<<poi[j].x<<' '<<poi[j].y<<endl;len[j][i]=distan(poi[i].x,poi[i].y,poi[j].x,poi[j].y);}}}
// __bug_len();rep(k,1,cntp){rep(i,1,cntp){rep(j,1,cntp){len[i][j]=min(len[i][j],len[i][k]+len[k][j]);}}}return len[1][cntp];
}int main()
{while(~scanf("%d",&n)){if(n==-1)break;init();cntp++;poi[cntp].x=0;poi[cntp].y=5;rep(i,1,n){double x;scanf("%lf",&x);double top,low;scanf("%lf",&top);cntp++;poi[cntp].x=x;poi[cntp].y=top;cntl++;lin[cntl].p.x=x;lin[cntl].p.y=0;lin[cntl].q.x=x;lin[cntl].q.y=top;scanf("%lf%lf",&low,&top);cntp++;poi[cntp].x=x;poi[cntp].y=top;cntp++;poi[cntp].x=x;poi[cntp].y=low;cntl++;lin[cntl].p.x=x;lin[cntl].p.y=low;lin[cntl].q.x=x;lin[cntl].q.y=top;scanf("%lf",&low);cntp++;poi[cntp].x=x;poi[cntp].y=low;cntl++;lin[cntl].p.x=x;lin[cntl].p.y=10;lin[cntl].q.x=x;lin[cntl].q.y=low;}cntp++;poi[cntp].x=10;poi[cntp].y=5;printf("%.2f\n",cal());
// __bug_len();}return 0;
}F POJ 2653 Pick-up sticks
Description
Stan has n sticks of various length. He throws them one at a time on the floor in a random way. After finishing throwing, Stan tries to find the top sticks, that is these sticks such that there is no stick on top of them. Stan has noticed that the last thrown stick is always on top but he wants to know all the sticks that are on top. Stan sticks are very, very thin such that their thickness can be neglected.
Input
Input consists of a number of cases. The data for each case start with 1 <= n <= 100000, the number of sticks for this case. The following n lines contain four numbers each, these numbers are the planar coordinates of the endpoints of one stick. The sticks are listed in the order in which Stan has thrown them. You may assume that there are no more than 1000 top sticks. The input is ended by the case with n=0. This case should not be processed.
Output
For each input case, print one line of output listing the top sticks in the format given in the sample. The top sticks should be listed in order in which they were thrown.
The picture to the right below illustrates the first case from input.
Sample Input
5
1 1 4 2
2 3 3 1
1 -2.0 8 4
1 4 8 2
3 3 6 -2.0
3
0 0 1 1
1 0 2 1
2 0 3 1
0
Sample Output
Top sticks: 2, 4, 5.
Top sticks: 1, 2, 3.
题意
某人往一个平面上扔木棍,问有多少根木棍是在最上层。
思路
暴力。叉积判断两线段是否相交。
坑点
写到这里的时候发现了我前几题的快速跨立实验是有问题的,在这里纠正了。
代码
#include <iostream>
#include <cstdio>
#include <cmath>using namespace std;const int N=100005;
const double EPS=1e-15;typedef long long ll;#define rep(i,a,b) for(int i=a;i<=b;i++)
#define per(i,a,b) for(int i=a;i>=b;i--)int n;struct P
{double x,y;
};struct S
{P p,q;
} sti[N];double cross(double x1,double y1,double x2,double y2,double x3,double y3)
{double DEBUG=(-x1*y2+x1*y3+x2*y1-x2*y3-x3*y1+x3*y2);return (-x1*y2+x1*y3+x2*y1-x2*y3-x3*y1+x3*y2);
}bool intersect_line(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4)
{bool ans;if(cross(x1,y1,x2,y2,x3,y3)*cross(x1,y1,x2,y2,x4,y4)>EPS||cross(x3,y3,x4,y4,x1,y1)*cross(x3,y3,x4,y4,x2,y2)>EPS)ans=false;elseans=true;return ans;
}bool intersect_seg(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4)
{//快速排斥实验bool ans=min(x1,x2)<=max(x3,x4)&&min(x3,x4)<=max(x1,x2)&&min(y1,y2)<=max(y3,y4)&&min(y3,y4)<=max(y1,y2);if(!ans)return false;//快速跨立实验if(cross(x1,y1,x2,y2,x3,y3)*cross(x1,y1,x2,y2,x4,y4)>EPS||cross(x3,y3,x4,y4,x1,y1)*cross(x3,y3,x4,y4,x2,y2)>EPS)ans=false;elseans=true;return ans;
}int main()
{while(~scanf("%d",&n)){if(n==0)break;rep(i,1,n){scanf("%lf%lf%lf%lf",&sti[i].p.x,&sti[i].p.y,&sti[i].q.x,&sti[i].q.y);}printf("Top sticks: ");int _flag=0;rep(i,1,n){int flag=1;rep(j,i+1,n){if(intersect_seg(sti[i].p.x,sti[i].p.y,sti[i].q.x,sti[i].q.y,sti[j].p.x,sti[j].p.y,sti[j].q.x,sti[j].q.y)==true){flag=0;break;}}if(flag){if(_flag==1)printf(", ");printf("%d",i);_flag=1;}}printf(".\n");}return 0;
}G POJ 1066 Treasure Hunt
Description
Archeologists from the Antiquities and Curios Museum (ACM) have flown to Egypt to examine the great pyramid of Key-Ops. Using state-of-the-art technology they are able to determine that the lower floor of the pyramid is constructed from a series of straightline walls, which intersect to form numerous enclosed chambers. Currently, no doors exist to allow access to any chamber. This state-of-the-art technology has also pinpointed the location of the treasure room. What these dedicated (and greedy) archeologists want to do is blast doors through the walls to get to the treasure room. However, to minimize the damage to the artwork in the intervening chambers (and stay under their government grant for dynamite) they want to blast through the minimum number of doors. For structural integrity purposes, doors should only be blasted at the midpoint of the wall of the room being entered. You are to write a program which determines this minimum number of doors.
An example is shown below:
Input
The input will consist of one case. The first line will be an integer n (0 <= n <= 30) specifying number of interior walls, followed by n lines containing integer endpoints of each wall x1 y1 x2 y2 . The 4 enclosing walls of the pyramid have fixed endpoints at (0,0); (0,100); (100,100) and (100,0) and are not included in the list of walls. The interior walls always span from one exterior wall to another exterior wall and are arranged such that no more than two walls intersect at any point. You may assume that no two given walls coincide. After the listing of the interior walls there will be one final line containing the floating point coordinates of the treasure in the treasure room (guaranteed not to lie on a wall).
Output
Print a single line listing the minimum number of doors which need to be created, in the format shown below.
Sample Input
7
20 0 37 100
40 0 76 100
85 0 0 75
100 90 0 90
0 71 100 61
0 14 100 38
100 47 47 100
54.5 55.4
Sample Output
Number of doors = 2
题意
给定一个100*100的正方形,里面有一个宝藏,正方形内有n面墙,每面墙的中间可以凿一个门,正方形的边缘都可以凿门,问最少需要凿几个门才可以取出宝藏。
思路
易知,门是否凿在中间不影响需要凿的门的个数,所以我们只需要遍历整个正方形的外围所有点,判断这个点和宝藏所连成的线段上有多少门即可。
坑点
想不到。
在此膜拜kuangbin大佬。
还有,,,我要是再忘写\n,我就是、、、(你们说啥就是啥!)
前面的模板中有漏洞,现已修改。
代码
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>using namespace std;const int N=35;
const double EPS=1e-15;typedef long long ll;#define rep(i,a,b) for(int i=a;i<=b;i++)
#define per(i,a,b) for(int i=a;i>=b;i--)int n;
int minn=0x3f3f3f3f;struct P
{double x,y;
};struct L
{P p,q;
} lin[N];double cross(double x1,double y1,double x2,double y2,double x3,double y3)
{return (-x1*y2+x1*y3+x2*y1-x2*y3-x3*y1+x3*y2);
}bool intersect_line(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4)
{bool ans;if(cross(x1,y1,x2,y2,x3,y3)*cross(x1,y1,x2,y2,x4,y4)>=-EPS||cross(x3,y3,x4,y4,x1,y1)*cross(x3,y3,x4,y4,x2,y2)>=-EPS)ans=false;elseans=true;return ans;
}bool intersect_seg(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4)
{//快速排斥实验bool ans=min(x1,x2)<=max(x3,x4)&&min(x3,x4)<=max(x1,x2)&&min(y1,y2)<=max(y3,y4)&&min(y3,y4)<=max(y1,y2);if(!ans)return false;//快速跨立实验if(cross(x1,y1,x2,y2,x3,y3)*cross(x1,y1,x2,y2,x4,y4)>=-EPS||cross(x3,y3,x4,y4,x1,y1)*cross(x3,y3,x4,y4,x2,y2)>=-EPS)ans=false;elseans=true;return ans;
}void cal(double x1,double y1,double x2,double y2)
{int ans=0;rep(i,1,n){if(intersect_seg(x1,y1,x2,y2,lin[i].p.x,lin[i].p.y,lin[i].q.x,lin[i].q.y)==true)ans++;}minn=min(minn,ans);
}int main()
{scanf("%d",&n);rep(i,1,n){scanf("%lf%lf%lf%lf",&lin[i].p.x,&lin[i].p.y,&lin[i].q.x,&lin[i].q.y);}double x,y;scanf("%lf%lf",&x,&y);rep(i,0,100){cal(x,y,0,i);cal(x,y,100,i);cal(x,y,i,0);cal(x,y,i,100);}printf("Number of doors = %d\n",minn+1);return 0;
}
H POJ 1410 Intersection
Description
You are to write a program that has to decide whether a given line segment intersects a given rectangle.
An example:
line: start point: (4,9)
end point: (11,2)
rectangle: left-top: (1,5)
right-bottom: (7,1)
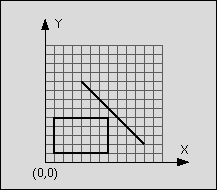
Figure 1: Line segment does not intersect rectangle
The line is said to intersect the rectangle if the line and the rectangle have at least one point in common. The rectangle consists of four straight lines and the area in between. Although all input values are integer numbers, valid intersection points do not have to lay on the integer grid.
Input
The input consists of n test cases. The first line of the input file contains the number n. Each following line contains one test case of the format:
xstart ystart xend yend xleft ytop xright ybottom
where (xstart, ystart) is the start and (xend, yend) the end point of the line and (xleft, ytop) the top left and (xright, ybottom) the bottom right corner of the rectangle. The eight numbers are separated by a blank. The terms top left and bottom right do not imply any ordering of coordinates.
Output
For each test case in the input file, the output file should contain a line consisting either of the letter “T” if the line segment intersects the rectangle or the letter “F” if the line segment does not intersect the rectangle.
Sample Input
1
4 9 11 2 1 5 7 1
Sample Output
F
题意
给定一个矩形和一条直线,问这个矩形和直线有没有公共部分,矩形包括边缘和矩形内部
思路
判断四条边和直线有没有交点,然后再判断直线有没有在矩形内部。
坑点
题目里面给的矩形不是左上角和右下角。。。
我之前的模板貌似没有错,,,但是对于不同的题目可能要稍微修改一下对EPS的确定,是>=-EPS还是>EPS。
代码
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>using namespace std;const int N=35;
const double EPS=1e-15;typedef long long ll;#define rep(i,a,b) for(int i=a;i<=b;i++)
#define per(i,a,b) for(int i=a;i>=b;i--)
#define ture trueint n;
int minn=0x3f3f3f3f;
bool ans=false;struct P
{double x,y;
};struct L
{P p,q;
} lin[N];double cross(double x1,double y1,double x2,double y2,double x3,double y3)
{return (-x1*y2+x1*y3+x2*y1-x2*y3-x3*y1+x3*y2);
}bool intersect_line(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4)
{bool ans;if(cross(x1,y1,x2,y2,x3,y3)*cross(x1,y1,x2,y2,x4,y4)>=-EPS||cross(x3,y3,x4,y4,x1,y1)*cross(x3,y3,x4,y4,x2,y2)>=-EPS)ans=false;elseans=true;return ans;
}bool intersect_seg(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4)
{//快速排斥实验bool ans=min(x1,x2)<=max(x3,x4)&&min(x3,x4)<=max(x1,x2)&&min(y1,y2)<=max(y3,y4)&&min(y3,y4)<=max(y1,y2);if(!ans)return false;//快速跨立实验if(cross(x1,y1,x2,y2,x3,y3)*cross(x1,y1,x2,y2,x4,y4)>EPS||cross(x3,y3,x4,y4,x1,y1)*cross(x3,y3,x4,y4,x2,y2)>EPS)ans=false;elseans=true;return ans;
}int main()
{int T;scanf("%d",&T);while(T--){ans=false;int x1,y1,x2,y2;int xx1,yy1,xx2,yy2;scanf("%d%d%d%d",&x1,&y1,&x2,&y2);scanf("%d%d%d%d",&xx1,&yy1,&xx2,&yy2);if(intersect_seg(x1,y1,x2,y2,xx1,yy1,xx2,yy1)==true)ans=true;if(intersect_seg(x1,y1,x2,y2,xx2,yy2,xx2,yy1)==true)ans=true;if(intersect_seg(x1,y1,x2,y2,xx1,yy2,xx2,yy2)==true)ans=true;if(intersect_seg(x1,y1,x2,y2,xx1,yy1,xx1,yy2)==true)ans=true;if(x1>=min(xx1,xx2)&&x1<=max(xx1,xx2)&&x2>=min(xx1,xx2)&&x2<=max(xx1,xx2)&&y1>=min(yy1,yy2)&&y1<=max(yy1,yy2)&&y1>=min(yy1,yy2)&&y2<=max(yy1,yy2))ans=true;if(ans==true)printf("T\n");elseprintf("F\n");}return 0;
}号外 极角排序板子题 POJ 2007 Scrambled Polygon
Description
A closed polygon is a figure bounded by a finite number of line segments. The intersections of the bounding line segments are called the vertices of the polygon. When one starts at any vertex of a closed polygon and traverses each bounding line segment exactly once, one comes back to the starting vertex.
A closed polygon is called convex if the line segment joining any two points of the polygon lies in the polygon. Figure 1 shows a closed polygon which is convex and one which is not convex. (Informally, a closed polygon is convex if its border doesn’t have any “dents”.)

The subject of this problem is a closed convex polygon in the coordinate plane, one of whose vertices is the origin (x = 0, y = 0). Figure 2 shows an example. Such a polygon will have two properties significant for this problem.
The first property is that the vertices of the polygon will be confined to three or fewer of the four quadrants of the coordinate plane. In the example shown in Figure 2, none of the vertices are in the second quadrant (where x < 0, y > 0).
To describe the second property, suppose you “take a trip” around the polygon: start at (0, 0), visit all other vertices exactly once, and arrive at (0, 0). As you visit each vertex (other than (0, 0)), draw the diagonal that connects the current vertex with (0, 0), and calculate the slope of this diagonal. Then, within each quadrant, the slopes of these diagonals will form a decreasing or increasing sequence of numbers, i.e., they will be sorted. Figure 3 illustrates this point.


Input
The input lists the vertices of a closed convex polygon in the plane. The number of lines in the input will be at least three but no more than 50. Each line contains the x and y coordinates of one vertex. Each x and y coordinate is an integer in the range -999…999. The vertex on the first line of the input file will be the origin, i.e., x = 0 and y = 0. Otherwise, the vertices may be in a scrambled order. Except for the origin, no vertex will be on the x-axis or the y-axis. No three vertices are colinear.
Output
The output lists the vertices of the given polygon, one vertex per line. Each vertex from the input appears exactly once in the output. The origin (0,0) is the vertex on the first line of the output. The order of vertices in the output will determine a trip taken along the polygon’s border, in the counterclockwise direction. The output format for each vertex is (x,y) as shown below.
Sample Input
0 0
70 -50
60 30
-30 -50
80 20
50 -60
90 -20
-30 -40
-10 -60
90 10
Sample Output
(0,0)
(-30,-40)
(-30,-50)
(-10,-60)
(50,-60)
(70,-50)
(90,-20)
(90,10)
(80,20)
(60,30)
题意
没啥题意,就极角排序排完输出就行。
思路
用叉积判断极角大小,写个cmp,sort一下就行。
坑点
无。
代码
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>using namespace std;const int N=55;
const double EPS=1e-15;typedef long long ll;#define rep(i,a,b) for(int i=a;i<=b;i++)
#define per(i,a,b) for(int i=a;i>=b;i--)
#define ture trueint n;
int minn=0x3f3f3f3f;
bool ans=false;struct P
{int x,y;
};int cross(int x1,int y1,int x2,int y2,int x3,int y3)
{return (-x1*y2+x1*y3+x2*y1-x2*y3-x3*y1+x3*y2);
}bool intersect_line(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4)
{bool ans;if(cross(x1,y1,x2,y2,x3,y3)*cross(x1,y1,x2,y2,x4,y4)>=-EPS||cross(x3,y3,x4,y4,x1,y1)*cross(x3,y3,x4,y4,x2,y2)>=-EPS)ans=false;elseans=true;return ans;
}bool intersect_seg(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4)
{//快速排斥实验bool ans=min(x1,x2)<=max(x3,x4)&&min(x3,x4)<=max(x1,x2)&&min(y1,y2)<=max(y3,y4)&&min(y3,y4)<=max(y1,y2);if(!ans)return false;//快速跨立实验if(cross(x1,y1,x2,y2,x3,y3)*cross(x1,y1,x2,y2,x4,y4)>EPS||cross(x3,y3,x4,y4,x1,y1)*cross(x3,y3,x4,y4,x2,y2)>EPS)ans=false;elseans=true;return ans;
}bool cmp(P aa,P bb)
{return cross(0,0,aa.x,aa.y,bb.x,bb.y)>=0;
}int main()
{P poi[N];int cnt_in=0;while(~scanf("%d%d",&poi[cnt_in].x,&poi[cnt_in].y)){cnt_in++;}sort(poi,poi+cnt_in,cmp);per(i,cnt_in-1,0){printf("(%d,%d)\n",poi[i].x,poi[i].y);}return 0;
}I POJ 1696 Space Ant
Description
The most exciting space discovery occurred at the end of the 20th century. In 1999, scientists traced down an ant-like creature in the planet Y1999 and called it M11. It has only one eye on the left side of its head and just three feet all on the right side of its body and suffers from three walking limitations:
It can not turn right due to its special body structure.
It leaves a red path while walking.
It hates to pass over a previously red colored path, and never does that.
The pictures transmitted by the Discovery space ship depicts that plants in the Y1999 grow in special points on the planet. Analysis of several thousands of the pictures have resulted in discovering a magic coordinate system governing the grow points of the plants. In this coordinate system with x and y axes, no two plants share the same x or y.
An M11 needs to eat exactly one plant in each day to stay alive. When it eats one plant, it remains there for the rest of the day with no move. Next day, it looks for another plant to go there and eat it. If it can not reach any other plant it dies by the end of the day. Notice that it can reach a plant in any distance.
The problem is to find a path for an M11 to let it live longest.
Input is a set of (x, y) coordinates of plants. Suppose A with the coordinates (xA, yA) is the plant with the least y-coordinate. M11 starts from point (0,yA) heading towards plant A. Notice that the solution path should not cross itself and all of the turns should be counter-clockwise. Also note that the solution may visit more than two plants located on a same straight line.

Input
The first line of the input is M, the number of test cases to be solved (1 <= M <= 10). For each test case, the first line is N, the number of plants in that test case (1 <= N <= 50), followed by N lines for each plant data. Each plant data consists of three integers: the first number is the unique plant index (1…N), followed by two positive integers x and y representing the coordinates of the plant. Plants are sorted by the increasing order on their indices in the input file. Suppose that the values of coordinates are at most 100.
Output
Output should have one separate line for the solution of each test case. A solution is the number of plants on the solution path, followed by the indices of visiting plants in the path in the order of their visits.
Sample Input
2
10
1 4 5
2 9 8
3 5 9
4 1 7
5 3 2
6 6 3
7 10 10
8 8 1
9 2 4
10 7 6
14
1 6 11
2 11 9
3 8 7
4 12 8
5 9 20
6 3 2
7 1 6
8 2 13
9 15 1
10 14 17
11 13 19
12 5 18
13 7 3
14 10 16
Sample Output
10 8 7 3 4 9 5 6 2 1 10
14 9 10 11 5 12 8 7 6 13 4 14 1 3 2
题意
一张图上有n个点,有一只只能往前和往左爬的蚂蚁,问这个蚂蚁爬完所有的点的路径。
思路
不停的极角排序。
坑点
cmp千万别写错!!!
代码
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>using namespace std;const int N=55;
const double EPS=1e-15;typedef long long ll;#define rep(i,a,b) for(int i=a;i<=b;i++)
#define per(i,a,b) for(int i=a;i>=b;i--)
#define ture trueint n;
int minn=0x3f3f3f3f;
bool ans=false;struct P
{int x,y;int id;
} poi[N];P cc;int cross(int x1,int y1,int x2,int y2,int x3,int y3)
{return (-x1*y2+x1*y3+x2*y1-x2*y3-x3*y1+x3*y2);
}bool intersect_line(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4)
{bool ans;if(cross(x1,y1,x2,y2,x3,y3)*cross(x1,y1,x2,y2,x4,y4)>=-EPS||cross(x3,y3,x4,y4,x1,y1)*cross(x3,y3,x4,y4,x2,y2)>=-EPS)ans=false;elseans=true;return ans;
}bool intersect_seg(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4)
{//快速排斥实验bool ans=min(x1,x2)<=max(x3,x4)&&min(x3,x4)<=max(x1,x2)&&min(y1,y2)<=max(y3,y4)&&min(y3,y4)<=max(y1,y2);if(!ans)return false;//快速跨立实验if(cross(x1,y1,x2,y2,x3,y3)*cross(x1,y1,x2,y2,x4,y4)>EPS||cross(x3,y3,x4,y4,x1,y1)*cross(x3,y3,x4,y4,x2,y2)>EPS)ans=false;elseans=true;return ans;
}double dist(P a,P b)
{return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}bool cmp(P aa,P bb)
{if(cross(cc.x,cc.y,aa.x,aa.y,bb.x,bb.y)>=-EPS&&cross(cc.x,cc.y,aa.x,aa.y,bb.x,bb.y)<=EPS)return dist(cc,aa)<dist(cc,bb);return cross(cc.x,cc.y,aa.x,aa.y,bb.x,bb.y)<0;
}int main()
{int T;scanf("%d",&T);while(T--){int n;scanf("%d",&n);rep(i,1,n){scanf("%d%d%d",&poi[i].id,&poi[i].x,&poi[i].y);if(poi[i].y<poi[1].y||(poi[i].y==poi[1].y&&poi[i].x<poi[1].x))swap(poi[i],poi[1]);}rep(i,2,n){cc=poi[i-1];sort(poi+i,poi+n+1,cmp);}printf("%d",n);rep(i,1,n){printf(" %d",poi[i].id);}printf("\n");}return 0;
}J POJ 3347 Kadj Squares
Description
In this problem, you are given a sequence S1, S2, …, Sn of squares of different sizes. The sides of the squares are integer numbers. We locate the squares on the positive x-y quarter of the plane, such that their sides make 45 degrees with x and y axes, and one of their vertices are on y=0 line. Let bi be the x coordinates of the bottom vertex of Si. First, put S1 such that its left vertex lies on x=0. Then, put S1, (i > 1) at minimum bi such that
bi > bi-1 and
the interior of Si does not have intersection with the interior of S1…Si-1.
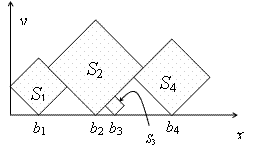
The goal is to find which squares are visible, either entirely or partially, when viewed from above. In the example above, the squares S1, S2, and S4 have this property. More formally, Si is visible from above if it contains a point p, such that no square other than Si intersect the vertical half-line drawn from p upwards.
Input
The input consists of multiple test cases. The first line of each test case is n (1 ≤ n ≤ 50), the number of squares. The second line contains n integers between 1 to 30, where the ith number is the length of the sides of Si. The input is terminated by a line containing a zero number.
Output
For each test case, output a single line containing the index of the visible squares in the input sequence, in ascending order, separated by blank characters.
Sample Input
4
3 5 1 4
3
2 1 2
0
Sample Output
1 2 4
1 3
题意
依次给了n个正方形,要求把这n个正方形依次与坐标轴成45度放置,问,从上往下看能看到多少正方形。
思路
记录正方形的左端点和边长(高度),然后对正方形的高度进行从上往下遍历,正方形左右端点间的距离就是从上往下看能看到的正方形的部分,然后记录上vis[ ],如果遍历到某一个正方形的某一个点的vis[ ]未被标记,则说明它之上没有正方形,也就是说这个正方形能被看到。
由于题中有个sqrt(2)的存在,容易造成精度问题,所以我们把所有边长都乘上sqrt(2),这样并不影响能否覆盖的相对位置,也能保证我们所需要的参数都是整数。
对于左端点的确定也比较简单,对之前已经放好的正方形进行遍历,所能满足条件的最大的左端点就是这个正方形的左端点。对于当前正方形 i 和所遍历到的正方形 j ,i 的左端点为sqr[j].left+2*sqr[j].heigh-abs(sqr[i].heigh-sqr[j].heigh),取最大值即可。
坑点
遍历左端点到右端点做标记的时候,rep(j,sqr[i].left+1,sqr[i].left+2*sqr[i].heigh),左端点需要+1
代码
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>using namespace std;typedef long long ll;#define rep(i,a,b) for(int i=a;i<=b;i++)
#define per(i,a,b) for(int i=a;i>=b;i--)const int N=55;struct S
{int heigh;int id;int left;int vis;
} sqr[N];int vis[N*1000];void init()
{memset(vis,0,sizeof(vis));
}bool cmp(S a,S b)
{return a.heigh<b.heigh;
}bool cmpp(S a,S b)
{return a.id<b.id;
}int main()
{int n;while(~scanf("%d",&n)){if(n==0) break;init();rep(i,1,n){scanf("%d",&sqr[i].heigh);sqr[i].id=i;sqr[i].vis=0;int maxn=0;rep(j,1,i-1){maxn=max(maxn,sqr[j].left+2*sqr[j].heigh-abs(sqr[i].heigh-sqr[j].heigh));}sqr[i].left=maxn;}sort(sqr+1,sqr+1+n,cmp);per(i,n,1){rep(j,sqr[i].left+1,sqr[i].left+2*sqr[i].heigh){if(vis[j]==0)sqr[i].vis=1;vis[j]=1;}}sort(sqr+1,sqr+1+n,cmpp);int flag=0;rep(i,1,n){if(sqr[i].vis==1){if(flag==1)printf(" ");flag=1;printf("%d",sqr[i].id);}}printf("\n");}return 0;
}K POJ 2826 An Easy Problem?!
Description
It’s raining outside. Farmer Johnson’s bull Ben wants some rain to water his flowers. Ben nails two wooden boards on the wall of his barn. Shown in the pictures below, the two boards on the wall just look like two segments on the plane, as they have the same width.
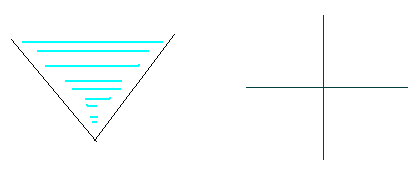
Your mission is to calculate how much rain these two boards can collect.
Input
The first line contains the number of test cases.
Each test case consists of 8 integers not exceeding 10,000 by absolute value, x1, y1, x2, y2, x3, y3, x4, y4. (x1, y1), (x2, y2) are the endpoints of one board, and (x3, y3), (x4, y4) are the endpoints of the other one.
Output
For each test case output a single line containing a real number with precision up to two decimal places - the amount of rain collected.
Sample Input
2
0 1 1 0
1 0 2 1
0 1 2 1
1 0 1 2
Sample Output
1.00
0.00
题意
给定两根木板,问这两根木板能接住多少水。
思路
直接暴力算。
坑点
从头到脚都是坑点。
所以我到现在都还没过。。。
代码
kuangbin大神的代码:
还有不知道为什么交G++就WA了,交C++就能AC,我决定放弃这一题了。。。
也搞不出啥名堂。。。
#include <stdio.h>
#include <math.h>
#include <algorithm>
#include <string.h>
#include <math.h>
using namespace std;const double eps = 1e-8;
int sgn(double x)
{if(fabs(x) < eps)return 0;if(x < 0)return -1;else return 1;
}
struct Point
{double x,y;Point(){}Point(double _x,double _y){x = _x;y = _y;}Point operator -(const Point &b)const{return Point(x - b.x,y - b.y);}//叉积double operator ^(const Point &b)const{return x*b.y - y*b.x;}//点积double operator *(const Point &b)const{return x*b.x + y*b.y;}
};
struct Line
{Point s,e;Line(){}Line(Point _s,Point _e){s = _s;e = _e;}//两直线相交求交点//第一个值为0表示直线重合,为1表示平行,为0表示相交,为2是相交//只有第一个值为2时,交点才有意义pair<int,Point> operator &(const Line &b)const{Point res = s;if(sgn((s-e)^(b.s-b.e)) == 0){if(sgn((s-b.e)^(b.s-b.e)) == 0)return make_pair(0,res);//重合else return make_pair(1,res);//平行}double t = ((s-b.s)^(b.s-b.e))/((s-e)^(b.s-b.e));res.x += (e.x-s.x)*t;res.y += (e.y-s.y)*t;return make_pair(2,res);}
};//*判断线段相交
bool inter(Line l1,Line l2)
{returnmax(l1.s.x,l1.e.x) >= min(l2.s.x,l2.e.x) &&max(l2.s.x,l2.e.x) >= min(l1.s.x,l1.e.x) &&max(l1.s.y,l1.e.y) >= min(l2.s.y,l2.e.y) &&max(l2.s.y,l2.e.y) >= min(l1.s.y,l1.e.y) &&sgn((l2.s-l1.e)^(l1.s-l1.e))*sgn((l2.e-l1.e)^(l1.s-l1.e)) <= 0 &&sgn((l1.s-l2.e)^(l2.s-l2.e))*sgn((l1.e-l2.e)^(l2.s-l2.e)) <= 0;
}int main()
{int x1,y1,x2,y2,x3,y3,x4,y4;int T;Line l1,l2;scanf("%d",&T);while(T--){scanf("%d%d%d%d%d%d%d%d",&x1,&y1,&x2,&y2,&x3,&y3,&x4,&y4);l1 = Line(Point(x1,y1),Point(x2,y2));l2 = Line(Point(x3,y3),Point(x4,y4));if(sgn(l1.s.y-l1.e.y)==0 || sgn(l2.s.y-l2.e.y) == 0){printf("0.00\n");continue;}if(sgn(l1.s.y-l1.e.y) < 0)swap(l1.s,l1.e);if(sgn(l2.s.y-l2.e.y) < 0)swap(l2.s,l2.e);if(inter(l1,l2) == false){printf("0.00\n");continue;}//口被封掉的情况if(inter(Line(l1.s,Point(l1.s.x,100000)),l2) ){printf("0.00\n");continue;}//口被封掉if(inter(Line(l2.s,Point(l2.s.x,100000)),l1) ){printf("0.00\n");continue;}pair<int,Point>pr;pr = l1 & l2;Point p = pr.second;double ans1;pr = l1 & Line(Point(100000,l2.s.y),l2.s);Point p1 = pr.second;ans1 = fabs( (l2.s-p)^(p1-p) )/2;double ans2;pr = l2 & Line(Point(100000,l1.s.y),l1.s);Point p2 = pr.second;ans2 = fabs( (l1.s-p)^(p2-p) )/2;printf("%.2lf\n",min(ans1,ans2));}return 0;
}
顺便也贴上我自己WA掉了的渣渣代码:
#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>using namespace std;typedef long long ll;#define rep(i,a,b) for(int i=a;i<=b;i++)
#define per(i,a,b) for(int i=a;i>=b;i--)const int N=110;
const double EPS=1e-12;int n;double cross(double x1,double y1,double x2,double y2,double x3,double y3)
{return (-x1*y2+x1*y3+x2*y1-x2*y3-x3*y1+x3*y2);
}bool intersect_line(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4)
{bool ans;if(cross(x1,y1,x2,y2,x3,y3)*cross(x1,y1,x2,y2,x4,y4)>-EPS)ans=false;elseans=true;return ans;
}bool intersect_seg(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4)
{//快速排斥实验bool ans=min(x1,x2)<=max(x3,x4)&&min(x3,x4)<=max(x1,x2)&&min(y1,y2)<=max(y3,y4)&&min(y3,y4)<=max(y1,y2);if(!ans) return false;//快速跨立实验if(cross(x1,y1,x2,y2,x3,y3)*cross(x1,y1,x2,y2,x4,y4)>-EPS)ans=false;elseans=true;return ans;
}int main()
{scanf("%d",&n);rep(cas,1,n){double x1,y1,x2,y2,x3,y3,x4,y4;scanf("%lf%lf%lf%lf%lf%lf%lf%lf",&x1,&y1,&x2,&y2,&x3,&y3,&x4,&y4);if(((y2-y1)*(x4-x3)-(y4-y3)*(x2-x1)>-EPS&&(y2-y1)*(x4-x3)-(y4-y3)*(x2-x1)<EPS)||y2==y1||y3==y4){printf("0.00\n");}else{if((y2-y1)*(x2-x1)>0&&(y4-y3)*(x4-x3)>0&&abs(y2-y1)*abs(x4-x3)>abs(y4-y3)*abs(x2-x1)&&max(x1,x2)>=max(x3,x4)){printf("0.00\n");}else if((y2-y1)*(x2-x1)>0&&(y4-y3)*(x4-x3)>0&&abs(y4-y3)*abs(x2-x1)>abs(y2-y1)*abs(x4-x3)&&max(x3,x4)>=max(x1,x2)){printf("0.00\n");}else if((y2-y1)*(x2-x1)<0&&(y4-y3)*(x4-x3)<0&&abs(y2-y1)*abs(x4-x3)>abs(y4-y3)*abs(x2-x1)&&max(x1,x2)<=max(x3,x4)){printf("0.00\n");}else if((y2-y1)*(x2-x1)<0&&(y4-y3)*(x4-x3)<0&&abs(y4-y3)*abs(x2-x1)>abs(y2-y1)*abs(x4-x3)&&max(x3,x4)<=max(x1,x2)){printf("0.00\n");}else{double ans_x=((x2-x1)*(y4-y3)*x3-(y2-y1)*(x4-x3)*x1+(y1-y3)*(x4-x3)*(x2-x1))/((y4-y3)*(x2-x1)-(y2-y1)*(x4-x3));double ans_y;if(!(x2-x1>=-EPS&&x2-x1<=EPS))ans_y=((y2-y1)/(x2-x1))*(ans_x-x1)+y1;elseans_y=((y4-y3)/(x4-x3))*(ans_x-x3)+y3;if(ans_x>=min(x1,x2)&&ans_x<=max(x1,x2)&&ans_y>=min(y1,y2)&&ans_y<=max(y1,y2)&&ans_x>=min(x3,x4)&&ans_x<=max(x3,x4)&&ans_y>=min(y3,y4)&&ans_y<=max(y3,y4)){double top=min(max(y1,y2),max(y3,y4));double xx1=(top-y1)*(x2-x1)/(y2-y1)+x1;double xx2=(top-y3)*(x4-x3)/(y4-y3)+x3;printf("%.2f\n",(top-ans_y)*abs(xx2-xx1)*0.5+EPS);}else{printf("0.00\n");}}}}return 0;
}要是有巨巨知道我哪里错了,请告诉我,不胜感激!
这篇关于大菜鸡的计算几何之旅-[kuangbin带你飞]专题十三 基础计算几何的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






