Pruning from Scratch 论文学习

本文主要是介绍Pruning from Scratch 论文学习，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Abstract

网络剪枝是降低神经网络计算成本的重要研究方向。传统的方法都是先训练一个大型、冗余的网络，然后决定哪些单元（如通道）没那么重要，可以被裁剪掉。这篇论文发现，我们不需要预训练一个过度参数化的网络，再对其进行剪枝。作者证明，从随机初始化的权重直接进行剪枝，可以获得更多样化的剪枝结构，甚至性能更优的模型。因而，作者提出了一个新的剪枝方法，允许我们从零开始剪枝 (prune from scratch)。在 CIFAR10 和 ImageNet 数据集上作者进行了分类模型的压缩实验，本文方法不仅极大地降低了传统剪枝方法中预训练的负担，而且在相同计算开支下，取得了相似的，甚至更高的准确率。本文的结果将促使该领域学者重新思考网络剪枝现有方法的有效性。

1. Introduction

由于深度神经网络被广泛应用在移动设备上，人们迫切地需要降低模型的大小和运行时延迟。因而人们提出了网络剪枝的方法，去除网络中的冗余结构和参数，实现模型压缩和推理加速。除了早期非结构化的剪枝方法，以通道剪枝为代表的结构化剪枝方法在近些年被普遍采用，因为它们在通用GPU上部署起来很方便。传统的网络剪枝方法采用了一个三阶段的流程，即预训练、剪枝和微调，如图1(a)。预训练和剪枝步骤可以循环交替进行。但是，最近的研究表明剪枝后的模型可以从零开始训练，无需对其进行微调（如图1(b)）。这就说明，剪枝后的网络结构对于剪枝模型的性能表现更重要。尤其是对于通道剪枝方法，我们应更加关注在每一层的通道数配置上。

尽管有人证明了，剪枝后模型的权重不需要进行微调，但我们仍需要依据不同的标准，从训练好的模型中学习和提取出剪枝后模型的结构。这个权重优化的过程通常很费时费力。那么就有个问题：从预训练模型中学习剪枝后的网络结构是否必要？

本文通过大量实验研究了这个问题，发现了一个令人吃惊的答案：我们并不需要从预训练权重中学习一个有效的剪枝结构。作者证明，从预训练权重中学到的剪枝结构都是类似的，这就限制了更优秀结构搜索的可能性。但对随机初始化权重直接进行剪枝，我们可以发现更多样化、更有效的剪枝结构，其中就有可能包含性能更佳的潜在模型。

基于以上发现，作者提出了一个新的网络剪枝方法，由随机初始化的权重直接学习剪枝网络结构，如图1c所示。特别地，作者利用了网络裁剪[19] 中相似的技巧，对每层都关联一个标量门值（scalar gate value），以此来学习通道的重要性。利用稀疏正则化对通道的重要性进行优化，提升模型性能。与之不同的地方就是，在此过程中本文没有更新随机权值。学习了通道重要性之后，本文利用了一个简单的二元搜索策略来决定在给定资源限制条件下（如 FLOPs），剪枝模型的通道数配置。由于本文方法不需要在优化阶段中更新模型的参数，搜索剪枝结构的速度非常快。在 CIFAR10 和 ImageNet 上的实验显示，本文的方法可以分别提升搜索的速度至少 10 倍和 100 倍，但取得的准确率和传统剪枝方法相比是差不多的，甚至要更好。此方法可以将研究人员从耗时的训练过程中解放出来，提供极具竞争力的剪枝结果。

2. Related Work

网络剪枝去除模型中冗余的参数和结构，对深度神经网络进行推理加速。早期有些工作提出了一些方法，去除单独的权重值，这就使网络变得非结构化稀疏。在单个GPU上实现运行时加速是比较有难度的，除非有一个定制化的推理引擎[6]。最近一些工作则关注在结构化模型剪枝[17,12,19]，尤其是对权重通道的剪枝。基于 $\mathcal{l}_1$ 范数的方法[17]根据权重通道的 $\mathcal{l}_1$ 范数进行模型剪枝。通道剪枝[12] 对局部层输出的重构损失最小化，学习稀疏权重。网络裁剪[19] 使用 LASSO 正则化来学习各通道的重要性，基于一个全局阈值来裁剪模型。自动模型压缩（AMC）[11] 通过增强学习自动地学习每层的压缩率，探索了剪枝策略。剪枝模型通常需要进一步微调，来取得更高的预测性能。但是，最近一些工作[4,20] 对此范式提出挑战，证明压缩模型可以从零开始训练，无需微调，也能取得类似的性能。

最近，神经结构搜索也给模型结构压缩提供了一个方向。[18,3 ] 延续了自上而下的模式，从一个大网络中裁剪出一个小网络。单阶段结构搜索方法[2,1]进一步发展了此思路，当学习了内部细胞连接重要性之后，进行结构搜索。但是这些方法都需要大量的训练时间，来搜索高效率的结构。

3. Rethinking Pruning with Pre-training

网络剪枝的目的是获取一个高效率剪枝网络，去除过度参数化的模型中存在的冗余参数或结构。代表性方法[19.5] 利用通道重要性来评估一个权重通道是否重要，是否应该被保留。给定一个预训练模型，每层都有一组通道门，学习通道的重要性。利用基于 $\mathcal{l}_1$ 范数的稀疏正则化来优化通道重要度。有了通道的重要度，我们用一个全局阈值来决定在给定资源的情况下，哪些通道应该保留。最终，剪枝模型可以用原始的完整模型权重来微调，也可以从零开始重新训练。整个流程如图1(a)和(b)所示。

接下来，作者将证明在网络剪枝的常用流程中，预训练的角色和我们之前所认为的有很大不同。基于此发现，作者提出了一个新的剪枝流程，允许剪枝网络从零（即随机初始化的权重）开始训练。

3.1 Effects of Pre-training on Pruning

传统剪枝流程中，我们似乎必须要先对网络进行充分地训练，然后再对其进行剪枝。这里作者仔细研究了预训练权重对最终的剪枝结构的作用。在训练基线网络时，作者保存了不同 epochs 的 checkpoints。然后用不同 checkpoints 的权重作为网络的初始化权重，使用上述流程，学习每一层的通道重要性。作者想要知道，不同阶段的预训练权重是否对最终的剪枝结构学习有重要影响。

3.2 Pruned Structure Similarity

首先，作者比较了不同剪枝模型的结构相似度。对于每个剪枝模型，计算每一层的剪枝比例，即剩余通道的个数除以原有通道的个数。将所有层的裁剪比例拼接起来，得到一个向量，然后将这个向量作为剪枝结构的特征表示。然后，计算这两个剪枝模型特征的相关系数，作为其结构的相似度。为了确保其有效，作者在 CIFAR10 数据集和 VGG16 数据集的实验中，随机选择了5组随机种子。在补充材料中，作者介绍了 ResNet20 和 ResNet56 的可视化结果。

图2展示了所有剪枝模型的相关系数矩阵。从该图，我们可以发现3个现象。首先，由随机权重学到的剪枝结构与所有预训练权重学到的网络结构都不一样（看图2(a),(b) 的左上图）。其次，由随机权重学到的剪枝模型结构要更加的多样化，相关系数更多样。同样，在预训练阶段 10个 epochs 的权重更新之后，剪枝模型趋向于同质化（看图2c）。第三，相近 epochs 的 checkpoints 得到的剪枝结构，其相关系数要更类似（看图2(a)(b)）。

上述结构相似的结果表明，在预训练阶段随着权重的更新，剪枝结构的搜索空间逐步缩小，可能会限制模型的潜在性能。另一方面，随机初始化的权重使得剪枝算法可以探索更多样化的剪枝结构。

3.3 Performance of Pruned Structures

作者进一步从头训练每个剪枝模型，比较其最终的准确率。表 1 列出了所有剪枝结构在 CIFAR10 测试集上的预测准确率。可以看到，随机权重的剪枝模型也可以取得和预训练权重得到的剪枝模型相同的表现。而且，在一些例子中（如 ResNet20），随机权重得到的剪枝模型甚至可以取得更高的准确率。这些结果证明，由随机权重直接学习得到的剪枝结构更加多样，而且也很有效，能够训练得到不错的效果。

剪枝模型的准确率表明，对于最终的预测性能而言，在预训练权重上得到的剪枝模型优势极其有限。预训练阶段的计算过程通常很耗时耗力，本文认为我们可以直接从随机初始化权重开始网络剪枝。

4. Our Solution: Pruning from Scratch

基于上述分析，作者提出了一个新的方法 “pruning from scratch”（从头开始训练）。和现有方法不同，它可以直接从随机初始化的权重中获取剪枝结构。

将一个深度神经网络记为 $\textbf{W}, \alpha)$ ，其中 $x$ 是输入样本， $\textbf{W}$ 是训练参数， $\alpha$ 是模型的结构。通常在 NAS 研究中， $\alpha$ 包括算子类型、数据流拓扑结构和各层超参数。在网络剪枝中，作者主要关注在微观的层设定上，尤其是通道剪枝策略中每层的通道个数。

为了高效地学习每层的通道重要度，我们在通道维度上，对第 $j$ 层关联一组标量门值 $\lambda_j$ 。该门值乘上该层的输出，进行逐通道的调整。因此，一个近似0的门值将会抑制对应通道的输出，完成剪枝。我们将 $K$ 层的标量门值记为 $\Lambda=\{\lambda_1, \lambda_2, ..., \lambda_K\}$ 。 $\Lambda$ 的优化目标函数为：

$\min_{\Lambda} \sum_{i}^N \mathcal{L}(f(x_i ; \textbf{W}, \Lambda), y_i) + \gamma \sum_j^K |\lambda_j|_1 \quad \textbf{s.t.} \quad 0\preceq \lambda_j \preceq 1, \forall j=1,2,...,K$

其中 $y_i$ 是对应的标签， $\mathcal{L}$ 是交叉熵损失， $\gamma$ 是平衡各项的乘数。这里，之前的工作主要有两方面。首先，在通道重要度学习阶段，我们并不更新权重；其次，我们使用随机初始化权重，不依赖于预训练。

按照网络裁剪中的方式，对于非平滑正则项，作者采用了二阶梯度下降的方法来优化 $\Lambda$ 。但是， $\mathcal{l}_1$ 范数会使得那些门变为0，不受任何约束，这样产生的剪枝结构不好。与网络裁剪论文的方程不同，本文利用所有门的平均值来近似其整体的稀疏比例，用平方范数将稀疏度逼近为预先定义的比值 $r$ [22]。因而，给定一个目标稀疏比值 $r$ ，正则项为：

$\Omega(\Lambda) = (\frac{\sum_j |\lambda_j|_1}{\sum_j C_j} - r)^2$

其中 $C_j$ 是第 $j$ 层的通道个数。根据实验，作者发现这项改进可以让剪枝结构更加合理。在优化过程中，可能存在多个门可以用于裁剪。作者选择其中稀疏度低于目标比值 $r$ ，但准确率最高的门作为最终的门。

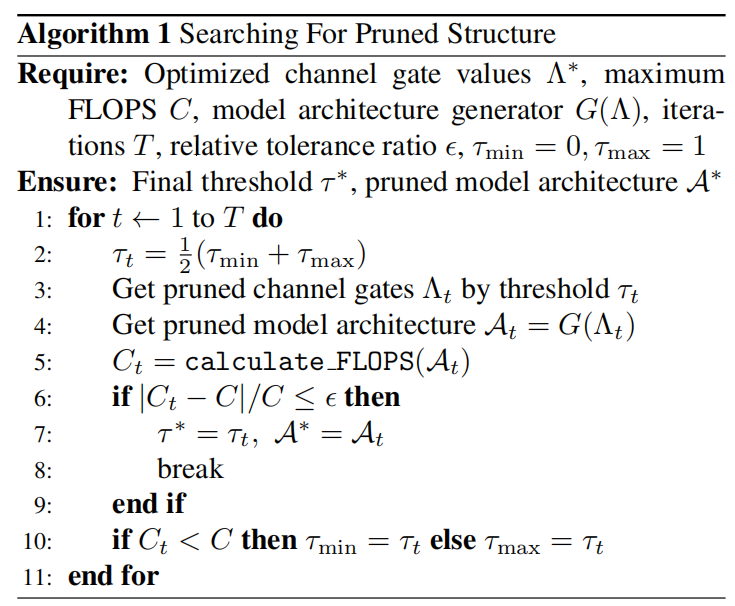
在得到一组优化了的门值后， $\Lambda^*=\{\lambda_1^*, \lambda_2^*, ..., \lambda_K^* \}$ ，选择一个阈值 $\tau$ 来决定哪些通道要被裁剪掉。在网络裁剪论文中，作者根据目标网络的参数量设定一个缩小比值，决定全局剪枝阈值。但是，一个更现实的方法是根据网络的 FLOPS 约束来找到剪枝结构。我们可以通过二元搜索法来决定全局阈值 $\tau$ ，直到剪枝结构满足条件限制。