本文主要是介绍伽马函数:将阶乘函数扩展到正整数之外,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

一、说明
,是对阶乘这种运算的实数域拓展。属于高级的数学模型,在高级概率模型用于定义分布函数。本文将介绍这个函数的基础概念和属性。
二、gamma函数定义
众所周知,阶乘这个运算本来是用于简化形如 n(n−1)(n−2)…3×2×1 的乘积的,但是经过几百年的发展,这个运算拓展到了复数域的,并拥有了新的名字——Gamma函数。
Gamma函数有很多定义,其中我们今天就来尝试从它的积分定义中推出其它定义:
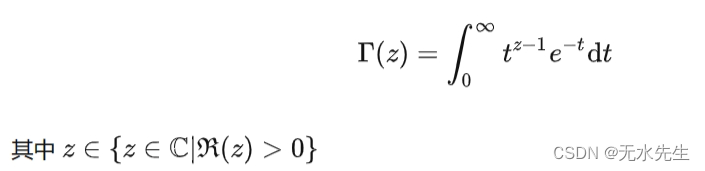
三、Gamma函数与阶乘的关系
倘若我们对这个函数分部积分,我们可以得到Gamma函数之间的关系:
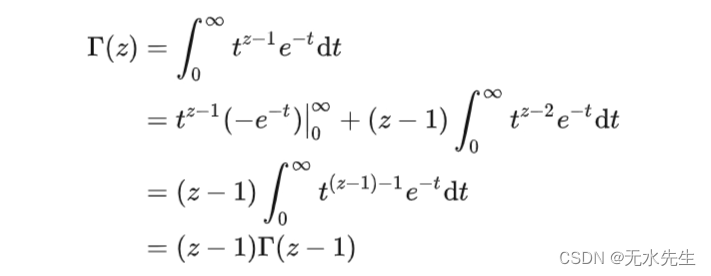
如果我们令z=1,则
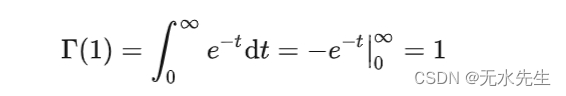
结合第一个结论,对于 ,存在:
![]()
于是我们得到Gamma函数与阶乘的联系 Γ(n)=(n−1)!
四、证明伽玛函数是阶乘的扩展
为了做到这一点,我们需要证明方程 Γ(n) = (n - 1)!对于定义阶乘函数的所有 n 的正整数都成立。由于不可能检查每个值,我们可以利用数学归纳原理一次检查所有值。
归纳证明的第一步是建立我们希望证明的命题:
![]()
现在,我们需要证明我们的基本情况成立,即当 n = 1 时。将其代入 gamma 函数的表达式中并计算:
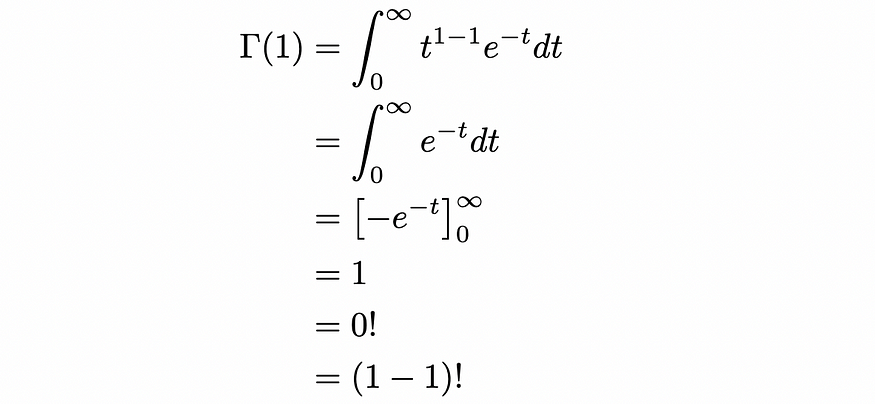
因此,基本情况 P(1) 为真。
归纳证明的下一步是归纳步骤,我们希望证明如果 P(k) 对某个正整数 k 成立,那么 P(k + 1) 也成立。为此,我们可以首先假设 P(k): Γ(k) = (k - 1)!是真的。考虑到这一点,我们可以尝试求解 Γ(k +1):
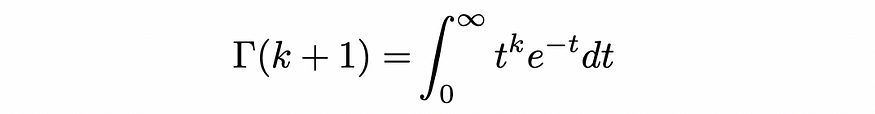
这个积分要求我们通过让u = t^k和dv = exp(-t)dt来使用部分积分。这给出了以下内容:
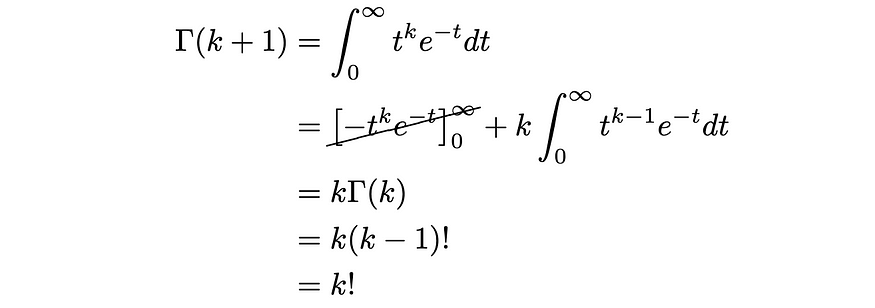
在倒数第二行中,我使用了我们的假设,即该命题适用于 P(k)。因此,我们刚刚证明,如果 P(k) 成立,那么 P(k + 1) 也会成立,并且由于我们的基本情况 P(1) 为真,根据数学归纳原理,任何正整数 n 的 P(n) 都必须为真。这表明,在正整数上,gamma 函数的行为确实与阶乘函数完全相同,如果我们考虑正整数以外的其他值,则可以证明它是阶乘的扩展。事实上,我们可以尝试使用 gamma 函数来尝试评估阶乘,例如 (1/2)!正如我将在下一节中介绍的那样。
五、计算(1/2)!
现在,在继续之前,重要的是要清楚,我们现在使用阶乘的 gamma 函数定义来评估这一点,因为原始定义没有很好地定义非整数值,例如 1/2。考虑到这一点,我们可以将 3/2 代入 gamma 函数来计算 1/2 的阶乘:
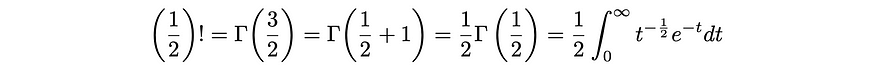
在第三步中,我利用了我们在归纳证明中展示的 Γ(k+1) = k Γ(k) 的事实。现在,右边的积分一开始肯定不明显,但我们可以通过使用 x = t^(1/2) 的代入将其转换为更熟悉的积分,得到 t = x² 和 dt = 2 t^(1/2)dx。将这两者代入,我们得到以下结果:
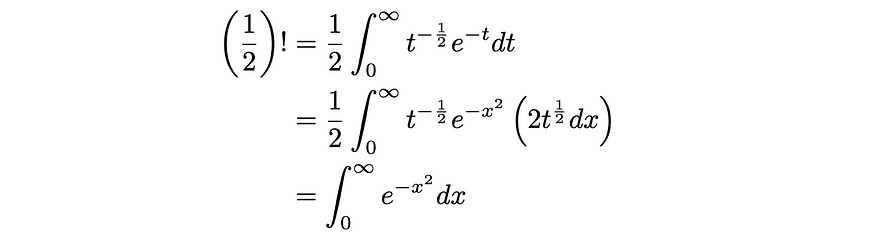
最后一个积分是著名的积分的形式,称为高斯积分,可以通过将积分转换为极坐标中的双积分来解决。如果您不熟悉这一点,我在这篇文章中介绍了解决高斯积分的方法,所以我建议您检查一下。现在,由于从 -∞ 到 ∞ 的这个积分的解是π的平方根,因此从 0 到 ∞ 的积分必须是这个积分的一半,因为它是一个偶数函数。因此,我们可以得出以下结论:
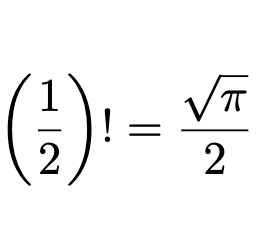
由于π在解决方案中,这当然是一个有趣且意想不到的结果。但是,重要的是要认识到这不是我们通常定义的阶乘,并且这仅在我们使用了扩展的伽马函数定义时才有效。此外,虽然我只研究了这个非整数有理数的例子,但 gamma 函数也是在所有复数值上定义的,其实部大于 0。事实上,我们实际上也可以使用一种称为复分析延续的技术,将域扩展到具有非正实部的(大多数)复数。如果您对这些进一步的扩展感到好奇,我绝对建议您在线对其进行进一步研究。感谢您的阅读。
六、gamma函数的python作图
########################
# f(x) = exp(-x) graph #
########################
import matplotlib.pyplot as plt
import numpy as np
# Create x and y
x = np.linspace(-2, 20, 100)
y = np.exp(-x)
# Create the plot
fig, ax = plt.subplots()
plt.plot(x, y, label='f(x) = exp(-x)', linewidth=3, color='palegreen')
# Make the x=0, y=0 thicker
ax.set_aspect('equal')
ax.grid(True, which='both')
ax.axhline(y=0, color='k')
ax.axvline(x=0, color='k')
# Add a title
plt.title('f(x) = exp(-x)', fontsize=20)
# Add X and y Label
plt.xlabel('x', fontsize=16)
plt.ylabel('f(x)', fontsize=16)
# Add a grid
plt.grid(alpha=.4, linestyle='--')
# Show the plot
plt.show()
####################
# f(x) = x^z graph #
####################
import matplotlib.pyplot as plt
import numpy as np
# Create x and y
x = np.linspace(0, 2, 100)
y1 = x**1.3
y2 = x**2.5
y3 = x**3.8
# Create the plot
fig, ax = plt.subplots()
plt.plot(x, y1, label='f(x) = x^1.3', linewidth=3, color='palegreen')
plt.plot(x, y2, label='f(x) = x^2.5', linewidth=3, color='yellowgreen')
plt.plot(x, y3, label='f(x) = x^3.8', linewidth=3, color='olivedrab')
# Make the x=0, y=0 thicker
ax.set_aspect('equal')
ax.grid(True, which='both')
ax.axhline(y=0, color='k')
ax.axvline(x=0, color='k')
# Add a title
plt.title('f(x) = x^z', fontsize=20)
# Add X and y Label
plt.xlabel('x', fontsize=16)
plt.ylabel('f(x)', fontsize=16)
# Add a grid
plt.grid(alpha=.4, linestyle='--')
# Add a Legend
plt.legend(bbox_to_anchor=(1, 1), loc='best', borderaxespad=1, fontsize=12)
# Show the plot
plt.show()
###############################
# f(x) = x^(3.8)*e^(-x) graph #
###############################
import matplotlib.pyplot as plt
import numpy as np
# Create x and y
x = np.linspace(0, 20, 100)
y = x**3.8 * np.exp(-x)
# Create the plot
fig, ax = plt.subplots()
plt.plot(x, y, label='f(x) = x^(3.8) * np.exp(-x)', linewidth=3, color='palegreen')
ax.fill_between(x, 0, y, color='yellowgreen')
# Make the x=0, y=0 thicker
ax.set_aspect('equal')
ax.grid(True, which='both')
ax.axhline(y=0, color='k')
ax.axvline(x=0, color='k')
# Add a title
plt.title('f(x) = x^(3.8)*e^(-x) ', fontsize=20)
# Add X and y Label
plt.xlabel('x', fontsize=16)
plt.ylabel('f(x)' ,fontsize=16)
# Add a grid
plt.grid(alpha=.4, linestyle='--')
# Add a Legend
plt.legend(bbox_to_anchor=(1, 1), loc='upper right', borderaxespad=1, fontsize=12)
# Show the plot
plt.show()结果如下:
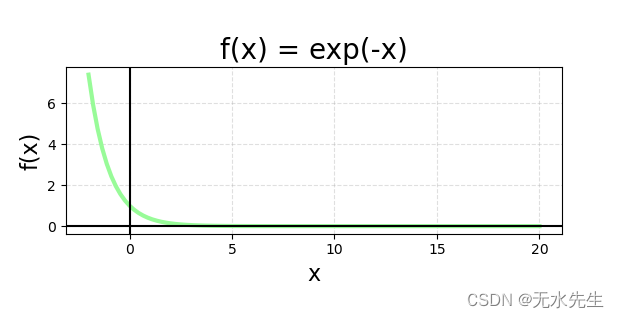
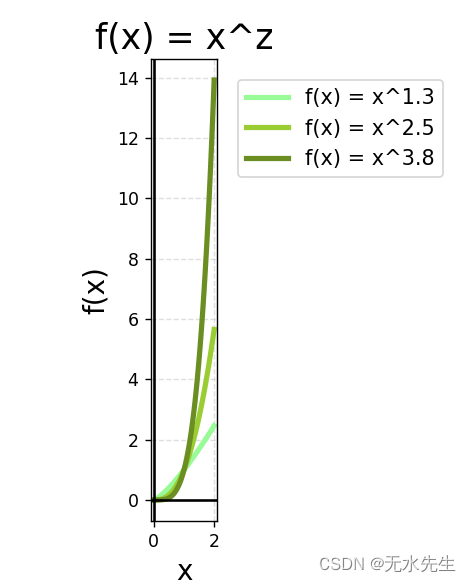
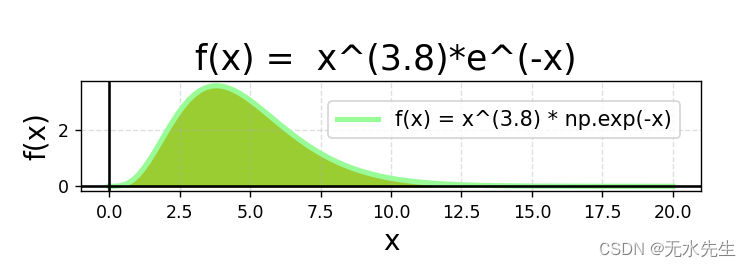
这篇关于伽马函数:将阶乘函数扩展到正整数之外的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




