本文主要是介绍三维模型表面积计算方法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
【版权声明】
本文为博主原创文章,未经博主允许严禁转载,我们会定期进行侵权检索。
更多算法总结请关注我的博客:https://blog.csdn.net/suiyingy,或”乐乐感知学堂“公众号。
本文章来自于专栏《Python三维模型处理基础》的系列文章,专栏地址为:https://blog.csdn.net/suiyingy/category_12462636.html。
在当今数字化时代,三维模型已经广泛应用于各个领域,如游戏开发、建筑设计、工程制图等。了解三维模型的表面积以及其计算方法,对于模型的几何特征分析和后续处理具有重要意义。本篇博文将带您深入了解三维模型表面积的定义、作用以及计算方法。
1 表面积定义
三维模型表面积是指模型所有外部表面的总面积。在数学上,它可以被视为一个多边形网格的组合,由许多个平面三角形组成。每个三角形都有自己的面积,将它们相加即可得到整个模型的表面积。
2 表面积作用
几何特征分析:表面积可以用于对三维模型的几何特征进行分析和描述。通过表面积,我们可以了解模型的大小、形状以及精细程度,从而为后续的评估和改进工作提供基础数据。
光照和渲染:在计算机图形学中,光照和渲染是模拟真实世界的重要步骤。表面积决定了模型的各个部分可以接收到多少光线,从而影响最终的视觉效果。计算表面积有助于优化渲染过程,提高图像质量和真实感。
物理仿真:在物理仿真中,表面积对于计算模型的质量、密度以及碰撞检测等方面非常重要。通过对表面积的计算,可以更准确地模拟模型的物理行为,提高仿真的准确性和真实度。
此外,上一节介绍的三维模型顶点法向量计算过程中加权求和的权重也由表面积来决定。
3 计算方法
计算三维模型表面积的方法有多种,这里介绍两种常用的方法,即多边形网格法和曲面拟合法。
多边形网格法的步骤为:
(1)首先,将三维模型表示为一个由多个小三角形组成的多边形网格。
(2)计算每个三角形的面积,可以使用海伦公式或矢量运算等方法。
(3)将所有三角形的面积相加,得到整个模型的表面积。
曲面拟合法的步骤为:
(1)首先,将三维模型表面离散化为一系列点云。
(2)使用曲面拟合算法,如Bezier曲线或B样条曲线,将点云拟合成光滑的曲面。
(3)计算拟合曲面的表面积。
需要注意的是,计算三维模型表面积的精确度与离散化程度相关。较为密集的网格或点云将提供更准确的结果,但也会增加计算复杂度和存储需求。
4 python示例程序
4.1 单个三角面
这里我们仍然采用trimesh和open3d来计算三维模型的表面积。我们首先以单个三角面为例,假设顶点坐标分别为[[0.0, 0.0, 1.0], [3.0, 0.0, 1.0], [0.0, 4.0, 1.0]]。显然,这是一个直角三角形,其面积为1/2 * 3 * 4 = 6。
Trimesh计算三维模型表面积的函数为mesh.area,上述三角面的计算结果为6.0,与预期理论结果一致。关键程序如下所示。
mesh = trimesh.Trimesh(vertices=vertices, faces=faces)
print('area result: ', mesh.area)Open3d计算三维模型表面积的函数为open3d.geometry.TriangleMesh.get_surface_area (Python method, in open3d.geometry.TriangleMesh),上述三角面的计算结果为6.0,与预期理论结果一致。关键程序如下所示。
mesh.vertices = o3d.utility.Vector3dVector(vertices)
mesh.triangles = o3d.utility.Vector3iVector(faces)
print('area result: ', mesh.get_surface_area())4.2 三棱柱表面积
假设三棱柱顶点和三角网格面分别为[[0.0, 0.0, 0.0], [3.0, 0.0, 0.0], [0.0, 4.0, 0.0], [0.0, 0.0, 5.0], [3.0, 0.0, 5.0], [0.0, 4.0, 5.0]]、[[1, 3, 2], [2, 3, 5], [5, 3, 6], [1, 4, 3], [3, 4, 6], [1, 2, 4], [2, 5, 4], [4, 5, 6]]。三棱柱示意图如下所示,底面是一个直角三角形。上下底面的面积均为6.0,三个侧面的面积依次为15.0、20.0、25.0,因此总面积为72.0。

图1 三棱柱模型
Trimesh和open3d相应表面积计算结果均为72.0。之前的博文介绍提到,三维模型的体积计算结果受到顶点顺序和封闭性影响。而三维模型的表面积则不受顶点顺序影响,并且仅计算三角网格的面积之和,孔洞不会自动补全或参与计算。
Trimesh可通过mesh.area_faces来获取各个三角面的面积,例如上述三棱柱对应的area_faces的计算结果为[ 6. 12.5 12.5 10. 10. 7.5 7.5 6. ]。
上述计算结果的详细Python示例程序下载地址为“https://download.csdn.net/download/suiyingy/88457956”,或者在”乐乐感知学堂“內回复”3d处理基础“即可。
此外,Cloud Compare也提供三维模型的表面积计算方法,其计算步骤为:首先加载并选中mesh模型,然后依次点击Edit->Mesh->Measure surface,如下图所示。

图2 Could Compare表面积计算过程
表面积计算结果会显示在下方提示区域,如下图所示。三棱柱表面积计算结果为S=72,与上述手动计算结果一致。
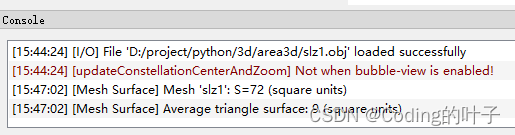
图3 Could Compare表面积计算结果
本篇博文介绍了三维模型表面积的定义、作用以及常用的计算方法。了解三维模型的表面积对于模型分析、渲染和仿真具有重要意义。通过计算表面积,我们可以更深入地理解三维模型的几何特征,并为相关领域的应用提供有力支持。希望本文能够帮助读者更好地理解和应用三维模型表面积的知识。
【版权声明】
本文为博主原创文章,未经博主允许严禁转载,我们会定期进行侵权检索。
更多算法总结请关注我的博客:https://blog.csdn.net/suiyingy,或”乐乐感知学堂“公众号。
本文章来自于专栏《Python三维模型处理基础》的系列文章,专栏地址为:https://blog.csdn.net/suiyingy/category_12462636.html。
这篇关于三维模型表面积计算方法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








