【算法】双轴快排

本文主要是介绍【算法】双轴快排，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

双轴快排

双轴快排是单轴快排的改进，初次学习双轴快排需要仔细深入地理解各处细节，因此本小节将详细介绍其实现细节，展示确定双轴位置既区间划分的过程。
前述快排每次递归确定当前区间的主轴，并利用该主轴将当前区间划分为左右两个部分。双轴快排则以两个轴 (pivot1, pivot2)将当前区间划分为三个子区间，双轴三区间的划分结果要满足如下。为方便叙述，将[left, pivot1)称作区间1，(pivot1, pivot2)称作区间2，(pivot2, right]称作区间3，其中pivot1，pivot2指的是最终位置，区间1，区间2，区间3均指划分后的最终区间。

arr[i] < arr[pivot1], i ∈ [left, pivot1) 区间1
arr[pivot1] ≤ arr[i] ≤ arr[pivot2], i ∈ (pivot1, pivot2) 区间2
arr[i] > arr[pivot2], i ∈ (pivot2, right] 区间3
对三个子区间执行同样的过程，直到无法划分时排序完成。算法主要过程和说明如下，结合后续代码实现的注释可准确把握各处细节。

dualPivotQuickSort执行开始，首先以if(left < right)为条件，只对大小大于等于2的区间执行双轴快排。

以如下语句令左右两端元素中较小者居左，后续以left为初始pivot1(下标)，right为初始pivot2(下标)，保证pivot1为左右两端元素中的较小者。

在程序后续内容中，arr[left]为pivot1的值(左轴值)，arr[right]为pivot2的值(右轴值)。

if(arr[left] > arr[right]) {
swap(arr, left, right);
}
设置index = left + 1，lower = left + 1，upper = right - 1。

index表示当前考察的元素下标。

lower是用于推进到pivot1最终位置的动态向右扩展的下标（扩展区间1），在程序的任意时刻总有[left, lower)的元素确定在区间1中。

upper是用于推进到pivot2最终位置的动态向左扩展的下标（扩展区间3），在程序的任意时刻总有(upper, right]的元素确定在区间3中。

当循环结束时lower–和upper++为最终的pivot1和pivot2的位置。
初始时lower == left + 1，表示区间1元素个数为1，
因为lower以左(不含lower)才是确定在区间1中的元素。
在遍历结束后以两个swap完成双轴归位时，
最后一个确定在区间1的元素会与arr[left]交换。
所以说我们一开始就知道left处的元素最终一定在区间1中，
因此初始时令lower == left + 1。
upper == right - 1的初始取值也是基于同样的原因。
如果现在还无法很好地理解这一点，先将整个过程看完后再回过头来多推敲几次。

从此处开始，代码行为是要遍历从left + 1到right - 1的所有元素，通过与arr[left] (左轴值)和arr[right] (右轴值)的比较，以及元素交换操作，将每一个元素正确地置于区间1，区间2和区间3中，与此同时，以lower的动态右移和upper的动态左移，不断扩展这三个区间。通过index++，从左到右依次遍历所有元素，当所有元素遍历完成，也就意味着所有元素都已归于其应属的区间。显然，这些操作应在一个循环之内，下面进入该循环。

首先，循环的边界条件是while(index <= upper)。虽然还未开始分析upper的动态变化，但已经知道upper以右(不含upper)的元素是确定在区间3中的，index向右推进的时候不能超过upper，因为下标为upper + 1的元素是已确定在区间3中的 (但下标为upper的元素尚未确定其归属)，所以是 <=。

以if(arr[index] < arr[left])考察arr[index]是否应在区间1，若满足则在区间1。这意味需要将该元素置于lower左侧，且区间1需向右扩展1位，通过如下两行，交换arr[index]和arr[lower]后lower++来完成。

swap(arr, index, lower); 
lower++;

类似地，以else if(arr[index] > arr[right])考察arr[index]是否应在区间3，若满足则在区间3。这意味着需要将该元素置于upper右侧，且区间3需向左扩展1位。与上一步(4.2)不同的是，不能直接执行如下两行，即交换arr[index]和arr[upper]后upper–。因为如果被交换的当前的arr[upper]也是应当位于区间3中的元素，交换后，继续考察下一个元素，且因为考察界满足index <= upper，将导致该元素无法再被考察，也就无法将其正确地放入区间3中。而上一步并不存在该问题（因为与arr[index]交换的arr[lower]一定是属于区间2的元素）。

swap(arr, index, upper);
upper--;

因此，在执行上述两行之前，应该实现一种操作，使得与arr[index]交换的arr[upper]不是区间3中的元素。于是可以先从当前arr[upper]往左考察是否有arr[upper] > arr[right]，若满足则表示arr[upper] 确定在区间3中，于是upper–扩展区间3，直到不满足时表示此时arr[upper]确定是不在区间3中的元素，于是才交换arr[index]和arr[upper]，然后upper–，如下。需要注意的是while中还有一个条件，即index < upper，因为区间3左扩不可使index == upper，否则之后的第二条upper–将导致upper为一个已经确定了区间归属的元素的位置（arr[index - 1]为已考察过元素）。

while(arr[upper] > arr[right] && index < upper) {upper--;
}
swap(arr, index, upper);
upper--;

如上，交换arr[index]和arr[upper]后，此时的arr[index]确定不在区间3中，但在区间1还是区间2中仍需明确，否则之后index++跳过该元素后将可能导致该元素归属错误。于是再对其执行一次与4.2相同的步骤。

if(arr[index] < arr[left]) {swap(arr, index, lower);lower++;
}

上述if和else if完成了对一个属于区间1和区间3元素考察和处理，不满足if且不满足else if的元素属于区间2，其已处于(lower, upper)之间，无需移动。
前述操作完成了对arr[index]的考察和处理（移动或不移动），于是index++，考察下一个元素。
当while(index <= upper)结束时，所有元素考察处理完毕，此时最后一个确定在区间1的元素下标是lower–，最后一个确定在区间3的元素下标是upper++。如下，通过交换将初始轴归于其正确的位置。最后对三个子区间分别递归地执行双轴快排。

lower--;
upper++;
swap(arr, left, lower);
swap(arr, upper, right);
dualPivotQuickSort(arr, left, lower - 1); // 区间1
dualPivotQuickSort(arr, lower + 1, upper - 1); // 区间2
dualPivotQuickSort(arr, upper + 1, right); // 区间3

下图展示了双轴快排对{29, 46, 21, 90, 14, 1, 68, 34, 55, 8}的双轴位置确定也即区间划分的过程。浅蓝色表示未排序，绿色表示左轴值，深蓝色表示右轴值，黄色表示区间1，灰色表示区间2，橙色表示区间3。
在这里插入图片描述

复杂度分析
时间复杂度：平均 / 最好为 O(nlogn)O(nlogn)，最坏为 O(n^2)O(n 2)。
单轴快排每次partition主轴均居中，则递归深度为 i 的partition有 2^i2 i 个，这 2^i2 i 个partition需要比较的次数是 (除去 2^{i-1}2 i−1 个主轴元素的元素个数) n - 2^{i-1}n−2 i−1 。给出如下复杂度估计。

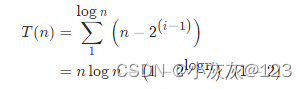
可知时间复杂度为 O(nlogn)O(nlogn)。

也可通过如下递推式导出。

T(n)=2 T(n / 2)+n

严格来说等号右边应该为 2T((n-1)/2)+n2T((n−1)/2)+n，因为确定轴之后轴元素不参与两分区划分，但并不影响结果的正确性，求解该递推式的方法在归并排序中已介绍过，最终同样得到时间复杂度为 O(nlogn)O(nlogn)。

双轴快排递推式如下，用同样的方法可得到 O(nlog_3n)O(nlog 3 n)。对数的底数为3，相比单轴快排的底数2，双轴快排的复杂度更低，效率更高。

最坏情形

对于单轴快排，当输入为已排序数组，且采用首位为主轴的方式，第 i 次partition后主轴左右两部分总是left = null，right = n - i, 第i次partition需要比较n - i次，共有n次partition，总比较次数 O(n^2)O(n 2 )。类似于对已排序的数组做选择排序。

左右两端取轴的双轴快排对于已排序数组，同样是 O(n^2)O(n 2 ) 的最坏情形。

空间复杂度：递归形式的快排，取决于递归深度，为 O(logn)O(logn)。非递归形式的快排，保存分区信息的栈深度与递归深度相同，空间复杂度也是 O(logn)O(logn)。

不同于归并排序中需要借助一个临时数组保存每次合并的结果，快速排序以原地交换元素的形式，避免了 O(n)O(n) 的数组开销。

代码

递归快排

// 三数取中快排
public int[] quickSortMedian3(int[] arr) {if (arr.length < 2) return arr;quickSortMedian3(arr, 0, arr.length - 1); // 后两个参数是下标值return arr;
}private void quickSortMedian3(int[] arr, int left, int right) {if (left < right) { // 执行median3将左，中，右三数中值放到left位置上median3(arr, left, right);int pivot = partition(arr, left, right);quickSortMedian3(arr, left, pivot - 1);quickSortMedian3(arr, pivot + 1, right);}
}/*** 三数取中方法* 将下标left到下标right的分区中，将left/center/right* 三者中的大小居中者放到当前分区的起始位置*/
private void median3(int[]arr, int left, int right) {int center = (left + right) / 2;// 第一个if，确保左和中这两个元素，大者居中if (arr[left] > arr[center]) {swap(arr, left, center);}// 第二个if，确保此时中和右这两个元素，大者居右// 前两个if，确保左中右这三个元素，大者居右if (arr[center] > arr[right]) {swap(arr, left, right);}// 第三个if，确保此时左和中这两个元素，大者居左// 三个if后，确保左中右这三个元素，中者居左if (arr[left] > arr[center]) return;else swap(arr, left, center);
}// 随机主轴快排
public int[] quickSortRandom(int[] arr) {if (arr.length < 2) {return arr;}quickSortRandom(arr, 0, arr.length - 1);return arr;
}private void quickSortRandom(int[] arr, int left, int right) {if (left < right) {// 取区间内随机下标，注意Random().nextInt(int x)方法的使用（含0不含x）int randomIndex = new Random().nextInt(right - left + 1) + left;// 交换随机取得的下标元素与当前起始元素swap(arr, left, randomIndex);int pivot = partition(arr, left, right);quickSortRandom(arr, left, pivot - 1);quickSortRandom(arr, pivot + 1, right);}
}// 朴素快排(首位为主轴)
public int[] quickSortSimple(int[] arr) {if (arr.length < 2) return arr;quickSortSimple(arr, 0, arr.length - 1); // 后两个参数是下标值return arr;
}private void quickSortSimple(int[] arr, int left, int right) {// 若left == right，表示此时arr只有一个元素，即为基准情形，完成递归(准确说是完成递进)// (尾递归，“回归”过程中不做任何事情）if (left < right) {int pivot = partition(arr, left, right);quickSortSimple(arr, left, pivot - 1);quickSortSimple(arr, pivot + 1, right);}
}//　partition方法
private int partition(int[] arr, int left, int right) {int pivot = left, index = pivot + 1;// 注意此时right是坐标，要执行到最后一个元素，所以是<=for (int i = index; i <= right; i++) {if (arr[i] < arr[pivot]) {swap(arr, index, i);index++;}}// 最后一个小于主轴元素的元素下标是index - 1swap(arr, pivot, index - 1);return index - 1;
}

非递归快排 (迭代快排)

public int[] quickSortStack(int[] arr) {// 用于保存区间左右边界的栈，按right到left的顺序将初始区间界入栈Deque<Integer> stack = new ArrayDeque<>();stack.push(arr.length - 1);stack.push(0);// 判断栈是否空，不空则弹出一对left，right界while(!stack.isEmpty()) {int left = stack.pop(), right = stack.pop();if(left < right) { // 执行partition的前提是left小于right// 对[left, right]区间执行partition方法，得到pivot// 加入后续两行实现随机轴快排// int randomIndex = new Random().nextInt(right - left + 1) + left;// swap(arr, left, randomIndex);// 加入下行实现三数取中快排median3(arr, left, right);int pivot = partition(arr, left, right);// 当前pivot的左区间存在则将该区间right，left界入栈if(pivot > left) {stack.push(pivot - 1);stack.push(left);}// 当前pivot的右区间存在则将该区间right，left界入栈if(right > pivot) {stack.push(right);stack.push(pivot + 1);}}}return arr;
}

双轴快排

public int[] dualPivotQuickSort(int[] arr) {if (arr.length < 2) return arr;dualPivotQuickSort(arr, 0, arr.length - 1); // 后两个参数是下标值return arr;
}
/**     区间1               区间2                         区间3* +------------------------------------------------------------+* |  < pivot1  | pivot1 <= && <= pivot2  |    ?    | > pivot2  |* +------------------------------------------------------------+*              ^                         ^         ^*              |                         |         |*            lower                     index      upper*/
private void dualPivotQuickSort(int[] arr, int left, int right) {if(left < right) { // 排序对象是right大于left的区间（即大小大于等于2的区间）// 令左右两端元素中较小者居左，以left为初始pivot1，right为初始pivot2// 即arr[left]为选定的左轴值，arr[right]为选定的右轴值if(arr[left] > arr[right]) {swap(arr, left, right);}int index = left + 1; // 当前考察元素下标int lower = left + 1; // 用于推进到pivot1最终位置的动态下标，总有[left, lower)确定在区间1中int upper = right - 1; // 用于推进到pivot2最终位置的动态下标，总有(upper, right]确定在区间3中// [lower, index)确定在区间2中，[index, upper]为待考察区间。// upper以右（不含upper）的元素都是确定在区间3的元素，所以考察元素的右界是upperwhile(index <= upper) {// 若arr[index] < arr[left]，即arr[index]小于左轴值，则arr[index]位于区间1if (arr[index] < arr[left]) {// 交换arr[index]和arr[lower]，配合后一条lower++，保证arr[index]位于区间1swap(arr, index, lower); // lower++，扩展区间1，lower位置向右一位靠近pivot1的最终位置lower++;}// 若arr[index] > arr[right]，即arr[index]大于右轴值，则arr[index]位于区间3else if(arr[index] > arr[right]) {// 先扩展区间3，使得如下while结束后upper以右（不含upper）的元素都位于区间3// 区间3左扩不可使index == upper，否则之后的第二条upper--将导致upper为一个已经确定了区间归属的元素的位置（即index - 1）while(arr[upper] > arr[right] && index < upper) {upper--;}// 交换arr[index]和arr[upper]，配合后一条upper--，保证arr[index]位于区间3swap(arr, index, upper);upper--;// 上述交换后，index上的数字已经改变，只知道此时arr[index] ≤ arr[right]，arr[index]有可能在区间1或区间2，// 若arr[index] < arr[left]，即arr[index]小于左轴值，则arr[index]位于区间1if(arr[index] < arr[left]) {// 交换arr[index]和arr[lower]，配合后一条lower++，保证arr[index]位于区间1swap(arr, index, lower);// lower++，扩展区间1，lower位置向右一位靠近pivot1的最终位置lower++;}}index++; // 考察下一个数字}// while(index <= upper)结束后最后一个确定在区间1的元素的下标是lower--，// 最后一个确定在区间3的元素下标是upper++。lower--;upper++;// 双轴归位。此时的lower，upper即分别为最终pivot1(初始时为left)，最终pivot2(初始时为right)。swap(arr, left, lower);swap(arr, upper, right);// 对三个子区间分别执行双轴快排dualPivotQuickSort(arr, left, lower - 1); // 区间1dualPivotQuickSort(arr, lower + 1, upper - 1); // 区间2dualPivotQuickSort(arr, upper + 1, right); // 区间3}
}

这篇关于【算法】双轴快排的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！