本文主要是介绍数学建模——最优管道分级铺设问题,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题目

题目条件
- 中心供水站只能和一级供水站连接(铺设I型管道),不能和二级供水站直接相连,但一级供水站之间可以连接(铺设I型管道)。I型管道使用1.6Mpa的DN250(10寸管),价格为571元/米,每米I型管道的铺设费用为720元。
- 一级供水站可以与二级供水站相连(铺设II型管道),且二级供水站之间也可以连接(铺设II型管道),II型管道使用1.6Mpa的DN125(5寸管),价格为235元/米,每米II型管道的铺设费用为210元。
- 各级供水站之间的连接管道必须从上一级供水站或同一级供水站的位置坐标出发,不能从管道中间的任意一点进行连接。
- 相邻两个供水站之间(如果有管道相连)所需管道长度可简化为欧氏距离。
- 受到一级供水站设备功率的影响,从一级供水站出发铺设的二级管道最多只能供水30公里,这条管道可以经过多个二级供水点,即按照该一级供水站管道输送的总里程计算。
问题求解
请您结合上述管道铺设要求建立模型讨论该地区最优输水管道建设方案,包括一级供水站的地址,I级管道和II级管道长度和分布,及最小费用等。
在这里,我将他们分为三个问题
问题一:选址问题,将180个点选出合适的一级点与二级点
问题二:一级管道与二级管道的长度和分布
问题三:最小费用
其实也可以分为两个问题,因为问题二求解出后,问题三就迎刃而解了。
问题一分析
首先,我们需要在180个点中找出一级供水站的数量和位置,因此我们先通过相关的选址模型进行筛选,在选址模型中,我们使用了覆盖模型,进而,我们使用了K-means聚类算法,将相关中心点确立为我们所需要的一级供水站的位置
问题二分析
问题二要求给出使管道总里程最小的铺设方案并且计算铺设管道的最小费用,这是一个最小生成树问题,可以分为三个步骤进行建模求解。步骤一是利用prim算法构造最小生成树模型求解管道的最小里程;步骤二是用Matlab软件编写代码,用欧式距离公式检验步骤一求出的管道是否符合“管道总里程最小”这一条件;步骤三是根据步骤一所求的I型管道、II级管道的最小里程和题目所给的管道信息求出铺设管道所用的总的最小费用。本问题的问题分析思路如下图所示:

思路
问题一思路
一开始用了三四种思路,比如p-中值选址,覆盖选址,遗传选址,最后还是用了聚类算法,进行聚点,比对了选取10,13,17,20个中心点的数据,发现在选取的这些数据中,17个中心点时能够有最优解,所以选用了17个中心点,这里的中心点即是一级供水站选点。
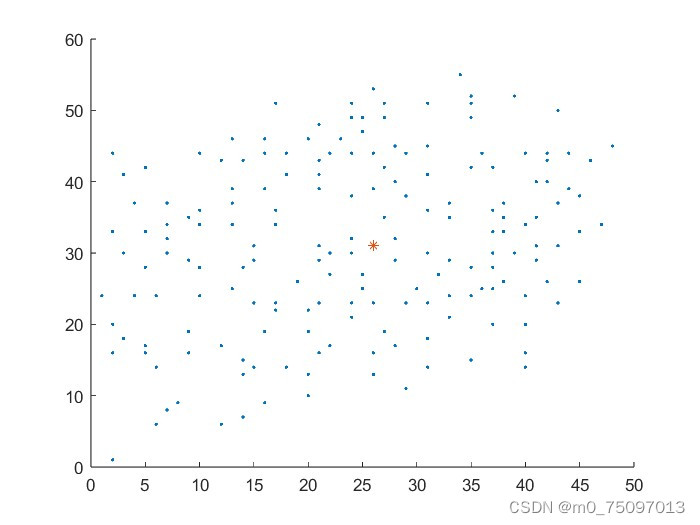
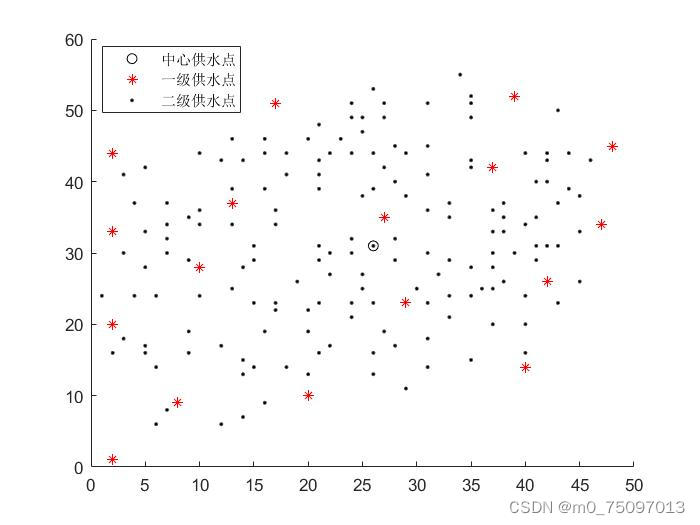
我们需要解决的问题是求解出一级供水站和二级供水站的分布情况,由于题目未给出一级供水站和二级供水站的具体数量和分布,我们首先应该将一级供水点与二级供水点的位置区分出来,并且确定各自的数量。这属于典型的选址问题,我们可以采用集合覆盖模型进行求解。
%先将181个点的散点图画出
V1=[5 8 10 13 17 20 25 31 35 36 41 45 41 40 38 38 33 31 33 28 24 21 22 28 43 44 25 21 22 24 37 38 37 14 16 14 18 12 15 20 13 16 21 26 28 27 29 29 36 41 39 27 23 20 6 22 40 42 37 35 35 35 34 26 27 31 31 31 28 27 24 26 13 17 21 18 21 13 14 12 10 16 18 24 25 24 24 21 17 10 9 7 4 5 2 7 7 1 2 3 2 4 5 6 9 2 7 3 3 10 17 20 24 22 21 27 26 9 12 14 19 14 13 9 2 6 7 6 5 5 16 26 29 31 28 20 17 15 21 24 26 25 15 15 10 38 37 33 40 44 41 33 32 40 42 45 29 31 30 31 35 40 40 37 35 43 45 37 35 33 37 39 41 43 47 46 42 48 42 43];
V2=[33 9 24 34 23 10 47 18 42 25 31 38 35 34 35 37 37 36 35 32 30 31 27 29 37 39 27 29 30 32 33 33 36 13 9 7 14 6 14 13 46 39 39 44 40 42 38 44 44 40 52 49 46 46 46 44 44 40 42 49 51 52 55 53 51 51 45 41 45 35 38 39 37 36 41 41 43 39 43 43 44 44 44 44 49 49 51 48 51 34 35 37 37 42 44 32 30 24 16 18 20 24 28 24 29 33 34 30 41 36 34 22 21 17 16 19 16 16 17 15 26 28 25 19 1 6 8 14 17 16 19 13 11 14 17 19 22 23 23 23 23 25 31 29 28 26 25 21 24 44 31 24 27 14 26 33 23 30 25 23 15 16 20 20 24 23 26 28 28 29 30 30 29 31 34 43 43 45 44 50];
scatter(V1,V2,'.') %画出180个点,以"'"表示
title('原始数据散点图')
hold on;
scatter(26,31,'*') %画出中心点,以"*"表示
hold on;%建立第一级、第二级最小树
%完成第一问
%最短里程是562.4008,第一级183.6268,第二级378.7740
clear;%清除工作区变量
clc;%清屏
close all;%关闭所有图形窗口%P139和V11重叠
A_x = 26;%中心点
A_y = 31;%中心点V_x = [27 2 8 2 13 40 20 48 29 37 2 2 47 39 17 10 42];%一级点
V_y = [35 44 9 33 37 14 10 45 23 42 20 1 34 52 51 28 26];%一级点P_x=[26 5 10 13 17 25 31 35 36 41 45 41 40 38 38 33 31 33 28 24 21 22 28 43 44 25 21 22 24 37 38 37 14 16 14 18 12 15 20 13 16 21 26 28 27 29 29 35 41 27 23 20 16 22 40 42 35 35 35 34 26 27 31 31 31 28 25 26 17 21 18 21 13 14 12 10 16 18 24 25 24 24 21 10 9 7 4 5 7 7 1 2 3 4 5 6 9 7 3 3 10 17 20 24 22 21 27 26 9 12 14 19 14 13 9 6 7 6 5 5 16 26 29 31 28 20 17 15 21 24 26 25 15 15 38 37 33 40 44 42 33 32 45 31 30 31 35 40 40 37 35 43 45 37 35 33 37 39 41 43 46 42 42 43];%二级点P_y=[31 33 24 34 23 47 18 42 25 31 38 35 34 35 37 37 36 35 32 30 31 27 29 37 39 27 29 30 32 33 33 36 13 9 7 14 6 14 13 46 39 39 44 40 42 38 44 43 40 49 46 46 46 44 44 40 49 51 52 55 53 51 51 45 41 45 38 39 36 41 41 43 39 43 43 44 44 44 44 49 49 51 48 34 35 37 37 42 32 30 24 16 18 24 28 24 29 34 30 41 36 34 22 21 17 16 19 16 16 17 15 26 28 25 19 6 8 14 17 16 19 13 11 14 17 19 22 23 23 23 23 25 31 29 26 25 21 24 44 31 24 27 33 30 25 23 15 16 20 20 24 23 26 28 28 29 30 30 29 31 43 43 44 50];%二级点
W = [A_x,A_y]; %中心供水站
V_point = [V_x' V_y']; %一级供水站
P_point = [P_x' P_y']; %二级供水站问题二思路
选取了中心点后,问题二的计算就比较简单了,用图论中的最小生成树,结合MATLAB,即可画图求解,算出最终结果。
1)建立带权的邻接矩阵
建立一个181行181列的矩阵z,其中第i行第j列的数值表示第i个供水站到第j个供水站的距离,由于中心供水站不能与二级供水站直接相连,每个供水站也不能与自身相连,故将此矩阵第一行的第 14 至第 181 列,第一列的第14至第181行和此矩阵主对角线上的所有元素置零。
2)建立中心供水站到所有一级供水站的最小生成树
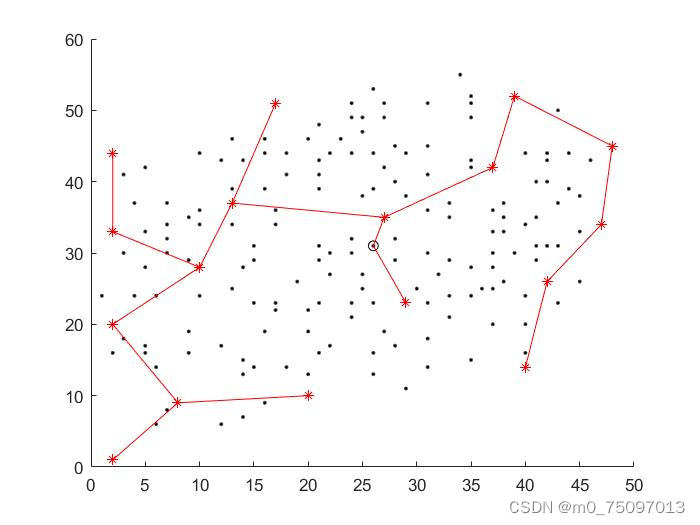
建立最小生成树有两种算法——Prim算法和Cruskal算法,在此处我们选择 Prim算法实现中心供水站到所有一级供水站的最小生成树,建立好的最小生成树如图5所示:
问题三思路
在问题二基础上,进行简单求解计算,得出结果
Num_I = 0; %I型管数目
Num_II = 0; %II型管数目
I_mileage = 0; %I型管里程
II_mileage = 0; %II型管里程
Total_mileage = 0; %总里程distance = 0; %两点距离
Shortest_distance = inf; %最短距离
abab = 0; %标号暂存
grade = 0; %标号暂存scatter(A_x,A_y,'ko') %画出散点图,中心点
hold on;
scatter(V_x,V_y,'r*') %一级点
hold on;
scatter(P_x,P_y,'k.') %二级点while size(V_point,1) %I型管道连接方式
Shortest_distance = inf;
for j = 1:1:size(W,1)for i = 1:1:size(V_point,1)distance = (W(j,1)-V_point(i,1))^2 + (W(j,2)-V_point(i,2))^2;distance = sqrt(distance);if Shortest_distance >= distanceShortest_distance = distance;abab= j;grade = i;endendendhold on;
plot([W(abab,1),V_point(grade,1)],[W(abab,2),V_point(grade,2)],'r');
Total_mileage = Total_mileage + Shortest_distance;
I_mileage = I_mileage + Shortest_distance;Num_I = Num_I+1;W = [W;V_point(grade,1),V_point(grade,2)];
V_point(grade,:) = [];
end W(1,:) = []; % 去掉中心供水站
WQ = W; % WQ和最初的V_point一样,但顺序不同while size(P_point,1) %II型管道连接方式Shortest_distance = inf;
for j = 1:1:size(WQ,1)for i = 1:1:size(P_point,1)distance = (WQ(j,1)-P_point(i,1))^2 + (WQ(j,2)-P_point(i,2))^2;distance = sqrt(distance);if Shortest_distance >= distanceShortest_distance = distance;abab= j;grade = i;endendend
hold on;
plot([WQ(abab,1),P_point(grade,1)],[WQ(abab,2),P_point(grade,2)],'k');
Total_mileage = Total_mileage + Shortest_distance;
II_mileage = II_mileage + Shortest_distance;
Num_II = Num_II+1;
WQ = [WQ;P_point(grade,1),P_point(grade,2)];
P_point(grade,:) = [];
endI_mileage %I型管总里程数
II_mileage %II型管总里程数
Total_mileage %管道总里程数优化
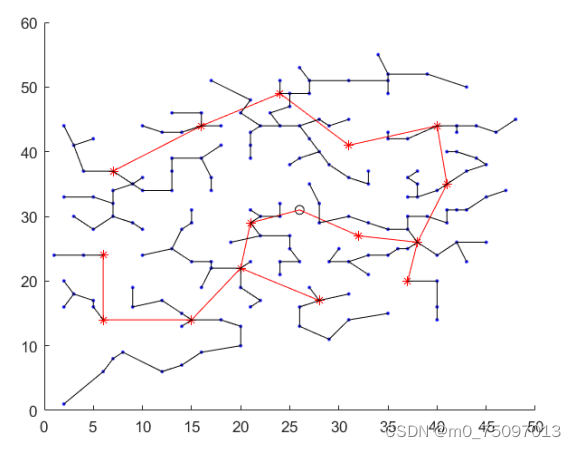
后来发现,选取聚点可能还是跨度过大了,用15个聚点时结果可能会更好。
附件
| 序号 | 类型 | X坐标 | Y坐标 | 序号 | 类型 | X坐标 | Y坐标 |
| 0 | A | 26 | 31 | 91 | P91 | 9 | 35 |
| 1 | P1 | 5 | 33 | 92 | P92 | 7 | 37 |
| 2 | P2 | 8 | 9 | 93 | P93 | 4 | 37 |
| 3 | P3 | 10 | 24 | 94 | P94 | 5 | 42 |
| 4 | P4 | 13 | 34 | 95 | P95 | 2 | 44 |
| 5 | P5 | 17 | 23 | 96 | P96 | 7 | 32 |
| 6 | P6 | 20 | 10 | 97 | P97 | 7 | 30 |
| 7 | P7 | 25 | 47 | 98 | P98 | 1 | 24 |
| 8 | P8 | 31 | 18 | 99 | P99 | 2 | 16 |
| 9 | P9 | 35 | 42 | 100 | P100 | 3 | 18 |
| 10 | P10 | 36 | 25 | 101 | P101 | 2 | 20 |
| 11 | P11 | 41 | 31 | 102 | P102 | 4 | 24 |
| 12 | P12 | 45 | 38 | 103 | P103 | 5 | 28 |
| 13 | P13 | 41 | 35 | 104 | P104 | 6 | 24 |
| 14 | P14 | 40 | 34 | 105 | P105 | 9 | 29 |
| 15 | P15 | 38 | 35 | 106 | P106 | 2 | 33 |
| 16 | P16 | 38 | 37 | 107 | P107 | 7 | 34 |
| 17 | P17 | 33 | 37 | 108 | P108 | 3 | 30 |
| 18 | P18 | 31 | 36 | 109 | P109 | 3 | 41 |
| 19 | P19 | 33 | 35 | 110 | P110 | 10 | 36 |
| 20 | P20 | 28 | 32 | 111 | P111 | 17 | 34 |
| 21 | P21 | 24 | 30 | 112 | P112 | 20 | 22 |
| 22 | P22 | 21 | 31 | 113 | P113 | 24 | 21 |
| 23 | P23 | 22 | 27 | 114 | P114 | 22 | 17 |
| 24 | P24 | 28 | 29 | 115 | P115 | 21 | 16 |
| 25 | P25 | 43 | 37 | 116 | P116 | 27 | 19 |
| 26 | P26 | 44 | 39 | 117 | P117 | 26 | 16 |
| 27 | P27 | 25 | 27 | 118 | P118 | 9 | 16 |
| 28 | P28 | 21 | 29 | 119 | P119 | 12 | 17 |
| 29 | P29 | 22 | 30 | 120 | P120 | 14 | 15 |
| 30 | P30 | 24 | 32 | 121 | P121 | 19 | 26 |
| 31 | P31 | 37 | 33 | 122 | P122 | 14 | 28 |
| 32 | P32 | 38 | 33 | 123 | P123 | 13 | 25 |
| 33 | P33 | 37 | 36 | 124 | P124 | 9 | 19 |
| 34 | P34 | 14 | 13 | 125 | P125 | 2 | 1 |
| 35 | P35 | 16 | 9 | 126 | P126 | 6 | 6 |
| 36 | P36 | 14 | 7 | 127 | P127 | 7 | 8 |
| 37 | P37 | 18 | 14 | 128 | P128 | 6 | 14 |
| 38 | P38 | 12 | 6 | 129 | P129 | 5 | 17 |
| 39 | P39 | 15 | 14 | 130 | P130 | 5 | 16 |
| 40 | P40 | 20 | 13 | 131 | P131 | 16 | 19 |
| 41 | P41 | 13 | 46 | 132 | P132 | 26 | 13 |
| 42 | P42 | 16 | 39 | 133 | P133 | 29 | 11 |
| 43 | P43 | 21 | 39 | 134 | P134 | 31 | 14 |
| 44 | P44 | 26 | 44 | 135 | P135 | 28 | 17 |
| 45 | P45 | 28 | 40 | 136 | P136 | 20 | 19 |
| 46 | P46 | 27 | 42 | 137 | P137 | 17 | 22 |
| 47 | P47 | 29 | 38 | 138 | P138 | 15 | 23 |
| 48 | P48 | 29 | 44 | 139 | P139 | 21 | 23 |
| 49 | P49 | 35 | 43 | 140 | P140 | 24 | 23 |
| 50 | P50 | 41 | 40 | 141 | P141 | 26 | 23 |
| 51 | P51 | 39 | 52 | 142 | P142 | 25 | 25 |
| 52 | P52 | 27 | 49 | 143 | P143 | 15 | 31 |
| 53 | P53 | 23 | 46 | 144 | P144 | 15 | 29 |
| 54 | P54 | 20 | 46 | 145 | P145 | 10 | 28 |
| 55 | P55 | 16 | 46 | 146 | P146 | 38 | 26 |
| 56 | P56 | 22 | 44 | 147 | P147 | 37 | 25 |
| 57 | P57 | 40 | 44 | 148 | P148 | 33 | 21 |
| 58 | P58 | 42 | 40 | 149 | P149 | 40 | 24 |
| 59 | P59 | 37 | 42 | 150 | P150 | 44 | 44 |
| 60 | P60 | 35 | 49 | 151 | P151 | 42 | 31 |
| 61 | P61 | 35 | 51 | 152 | P152 | 33 | 24 |
| 62 | P62 | 35 | 52 | 153 | P153 | 32 | 27 |
| 63 | P63 | 34 | 55 | 154 | P154 | 40 | 14 |
| 64 | P64 | 26 | 53 | 155 | P155 | 42 | 26 |
| 65 | P65 | 27 | 51 | 156 | P156 | 45 | 33 |
| 66 | P66 | 31 | 51 | 157 | P157 | 29 | 23 |
| 67 | P67 | 31 | 45 | 158 | P158 | 31 | 30 |
| 68 | P68 | 31 | 41 | 159 | P159 | 30 | 25 |
| 69 | P69 | 28 | 45 | 160 | P160 | 31 | 23 |
| 70 | P70 | 27 | 35 | 161 | P161 | 35 | 15 |
| 71 | P71 | 25 | 38 | 162 | P162 | 40 | 16 |
| 72 | P72 | 26 | 39 | 163 | P163 | 40 | 20 |
| 73 | P73 | 13 | 37 | 164 | P164 | 37 | 20 |
| 74 | P74 | 17 | 36 | 165 | P165 | 35 | 24 |
| 75 | P75 | 21 | 41 | 166 | P166 | 43 | 23 |
| 76 | P76 | 18 | 41 | 167 | P167 | 45 | 26 |
| 77 | P77 | 21 | 43 | 168 | P168 | 37 | 28 |
| 78 | P78 | 13 | 39 | 169 | P169 | 35 | 28 |
| 79 | P79 | 14 | 43 | 170 | P170 | 33 | 29 |
| 80 | P80 | 12 | 43 | 171 | P171 | 37 | 30 |
| 81 | P81 | 10 | 44 | 172 | P172 | 39 | 30 |
| 82 | P82 | 16 | 44 | 173 | P173 | 41 | 29 |
| 83 | P83 | 18 | 44 | 174 | P174 | 43 | 31 |
| 84 | P84 | 24 | 44 | 175 | P175 | 47 | 34 |
| 85 | P85 | 25 | 49 | 176 | P176 | 46 | 43 |
| 86 | P86 | 24 | 49 | 177 | P177 | 42 | 43 |
| 87 | P87 | 24 | 51 | 178 | P178 | 48 | 45 |
| 88 | P88 | 21 | 48 | 179 | P179 | 42 | 44 |
| 89 | P89 | 17 | 51 | 180 | P180 | 43 | 50 |
| 90 | P90 | 10 | 34 | ||||
这篇关于数学建模——最优管道分级铺设问题的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






