预测海藻数量

基于R语言 DMwR包的训练数据集。本案例涉内容：数据可视化，描述性统计分析，处理缺失值，回归分析，多元线性回归，回归树，K折交互验证选择和比较模型，模型组合和随机森林。

                                   预测海藻数量

一、问题描述与目标

      河流中某些高浓度有害藻类对河流生态环境有极大破坏力，严重影响河流生物及水质。本案例的目的是利用模型了解影响海藻的频率和水样的化学性质及其他特效（如季节、河流类型等）的相关性。

二、数据说明

      有两个数据集，第一个数据集有200个水样。该数据集的每一条记录是同一条河流在该年的同一个季节的三个月内收集的水样的平均值。 每条记录由11个变量构成。其中3个变量是名义变量，它们分别描述水样收集的季节、收集河流的大小和河水速度。余下的8个变量是所观察水样的不同化学参数，即最大pH值、最小含氧量（O2）、平均氯化物含量(cl)、平均硝酸盐含量(NO3)、平均氨含量(NH4)、平均正磷酸含量(PO4)、平均磷酸盐含量(PO4)、平均叶绿素含量。与这些参数相关的是7种不同有害藻类在相应水样中的频率数目。并未提供所观察藻类的名称的有关信息。

      第二个数据集由140个额外观察值构成。它们的基本结构和第一个数据集一样，但是它不包含7种藻类的频率数目。本案例的主要目的是预测140个水样中7种藻类的频率。

在这种问题中，任务是建立预测模型，并预测在给定预测变量的取值时相应的目标变量的值。预测模型也可能会说明哪一个预测变量对目标变量有较大的影响，即模型可能提供影响目标变量因素的一个综合描述。

 三、探索性变量分析（多种可视化）

 1、观察数据

> head(algae)

2、描述性统计

> summary(algae)

3、单变量分析（mxPH)

> library("car", lib.loc="~/R/win-library/3.3")
> par(mfrow=c(1,2))
> hist(algae$mxPH,prob=T,xlab = " ",main="MXPh",ylim = 0:1)
> lines(density(algae$mxPH,na.rm = T))
> rug(jitter(algae$mxPH))
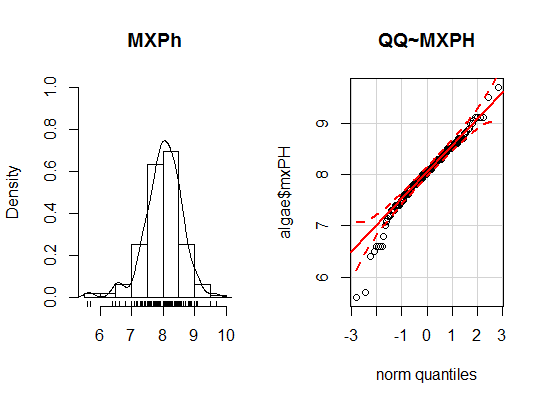
> qq.plot(algae$mxPH,main="QQ~MXPH")

 从左图可以看出变量mxPH基本呈正态分布，符合统计分析的需要。右图为mxPH变量值和正态分布的理论分位数（红色实线）的点散图。同时给出了正态分布95%置信区间的带状图（虚线），可以看出左下有几个小点明显在95%置信区间之外，不服从正态分布。

4、变量分析（oPO4)

> boxplot(algae$oPO4,ylab="oPO4")
> rug(jitter(algae$oPO4),side = 2)
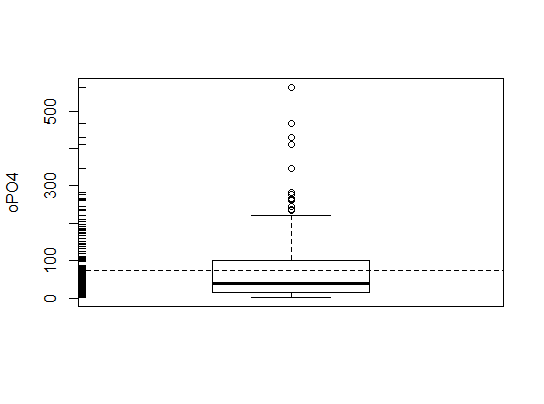
> abline(h= mean(algae$oPO4,na.rm = T),lty =2)

变量oPO4的分布集中在较小的观察值范围，因此分布为正偏，大部分水样的oPO4值比较低，但也有几个水样的观测值较高，甚至特别高。

5、变量分析（NH4）

> plot(algae$NH4,xlab = " ")
> abline(h=mean(algae$NH4,na.rm = T),lty=1)
> abline(h=mean(algae$NH4,na.rm = T)+sd(algae$NH4,na.rm = T),lty=2)
> abline(h=median(algae$NH4,na.rm = T),lty=3)
> identify(algae$NH4)
警告: 已经找到了最近的点
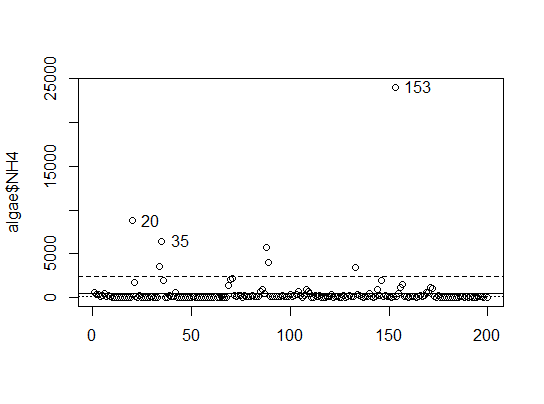
[1]  20  35 153

调用identify()函数，使图形可交互，点击图中的点可以查看点在数据中的行号，以便于查找离群数据的详细信息和位置。

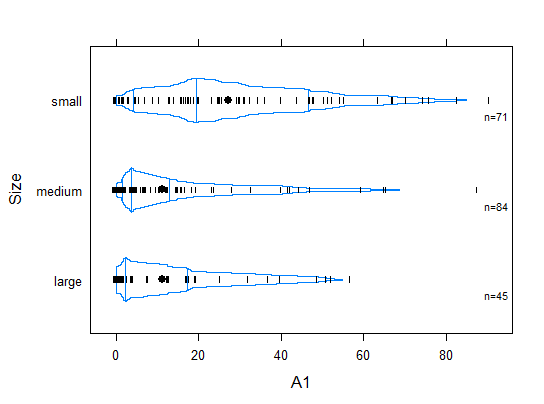
6、名义变量size（河流大小）对变量A1的影响分析。

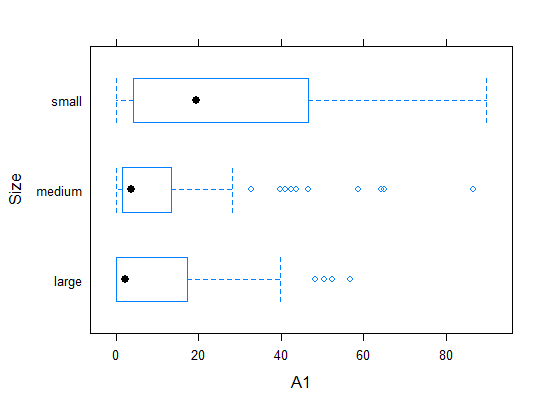
bwplot(size~a1,data=algae,ylab = "Size",xlab = "A1")

通过lattice版本的箱图可知，在规模较小的河流中。海藻a1 的频率较高。

下面通过分位箱图获得变量的更多信息。

bwplot(size~a1,data = algae,panel = panel.bpplot,probs=seq(.01,.49,by=.01),datadensity=TRUE,ylab = "Size",xlab = "A1"
+ )

小型河流有更高的海藻频率。但小型河流海藻频率的分布比其他类型河流的海藻频率分布更分散。

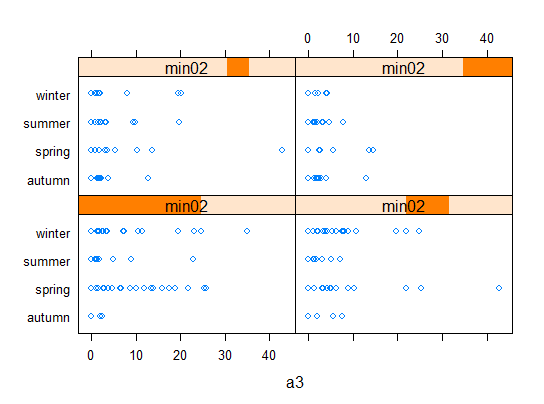
7、连续变量mn02处理和分析

> min02 <- equal.count(na.omit(algae$mnO2),number=4,overlap=1/5)
> stripplot(season~a3 | min02,data=algae[!is.na(algae$mnO2),])

调用equal.count( )函数对连续变量mno2离散化，把该变量转换为因子类型。参数number设置需要的区间个数，参数overlap设置俩个区间之间的靠近边界的重合，这意味这某些观测值将被分配到相邻的区间中，每个区间的观测值的个数相等。注意到，变量algae$mno2中含有NA值，为避免图形出错利用na.omit（）函数将其中的NA值剔除。

四、数据缺失值的处理

一些变量中含有缺失值，缺失值会严重影响数据分析的结果。所以必须对缺失值进行处理，可以运用以下几种常见的策略进行处理。

（1）将含有缺失值的数据删除。

（2）根据变量之间的相关关系填补缺失值。

（3）根据案例之间的相似性填补缺失值。

1、将缺失部分剔除

查看有缺失值的数据。

> algae[!complete.cases(algae),]season   size  speed mxPH mnO2    Cl   NO3 NH4    oPO4     PO4  Chla
28  autumn  small   high 6.80 11.1 9.000 0.630  20   4.000      NA  2.70
38  spring  small   high 8.00   NA 1.450 0.810  10   2.500   3.000  0.30
48  winter  small    low   NA 12.6 9.000 0.230  10   5.000   6.000  1.10
55  winter  small   high 6.60 10.8    NA 3.245  10   1.000   6.500    NA
56  spring  small medium 5.60 11.8    NA 2.220   5   1.000   1.000    NA
57  autumn  small medium 5.70 10.8    NA 2.550  10   1.000   4.000    NA
58  spring  small   high 6.60  9.5    NA 1.320  20   1.000   6.000    NA
59  summer  small   high 6.60 10.8    NA 2.