Matlab拟合工具箱拟合轮胎侧偏刚度

本文主要是介绍Matlab拟合工具箱拟合轮胎侧偏刚度，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Matlab拟合工具箱拟合轮胎侧偏刚度

使用matlab曲线拟合工具对轮胎侧偏刚度进行拟合

1.拟合工具箱（二维）

数据读取
从Carsim中获取轮胎数据，用Matlab进行读取，代码如下

%% 数据读取
slip_angle = xlsread('Fy_215_55_R17_TireData','Tire_Data','A2:A52');
FZ = xlsread('Fy_215_55_R17_TireData','Tire_Data','B1:I1');
y1 = xlsread('Fy_215_55_R17_TireData','Tire_Data','B2:B52');
y2 = xlsread('Fy_215_55_R17_TireData','Tire_Data','D2:D52');

拟合工具箱在如下位置：在这里插入图片描述
打开后页面如下：

导入数据后：

注：当我们不知道X与Y什么关系的时候，可以用自带的多项式拟合工具进行拟合
如果知道拟合公式，可以用下面方法写入公式，让其确定公式中的系数
这里参考论文《基于“魔术公式”的轮胎动力学仿真分析_郑香美》中的轮胎魔术公式，我们来确定其中的系数。公式如下，在工具箱中写入公式：
在这里插入图片描述

这里我们没有见到拟合曲线的出现，观察公式Fy=Dysin(Cyatan(Byx-Ey(Byx-atan(Byx))))+Sv可以看到,Fy=Dy*sin(XXXX)，其中sin()的最大值为1，而需要拟合的数据集最大有1500左右，这里我们需要给Dy赋个初值1500 就能看到拟合曲线了。
在这里插入图片描述
在左下Results中可以看到各个系数的拟合结果：

	   By =      0.2227  (0.2221, 0.2232)Cy =       1.411  (1.41, 1.413)Dy =        1593  (1590, 1595)Ey =     -0.2808  (-0.297, -0.2647)Sv =     -0.5206  (-2.59, 1.549)

导入数据y2，进行拟合，拟合结果如下
在这里插入图片描述

2.拟合工具箱（三维）

数据读取
从Carsim中获取轮胎数据，用Matlab进行读取，代码如下

clc;close all;clear;
%% 数据读取
slip_angle = xlsread('Fy_215_55_R17_TireData','Tire_Data','A2:A52');
FZ = xlsread('Fy_215_55_R17_TireData','Tire_Data','B1:I1');
y1 = xlsread('Fy_215_55_R17_TireData','Tire_Data','B2:B52');
y2 = xlsread('Fy_215_55_R17_TireData','Tire_Data','C2:C52');
y3 = xlsread('Fy_215_55_R17_TireData','Tire_Data','D2:D52');
y4 = xlsread('Fy_215_55_R17_TireData','Tire_Data','E2:E52');
zz = xlsread('Fy_215_55_R17_TireData','Tire_Data','B2:I52');
[x,y] = meshgrid(slip_angle,FZ);
z = zz';
mesh(x,y,z)

读取数据，同时画出三维曲面，如下：
在这里插入图片描述
打开工具箱，导入数据，这里导入的是原始数据

写入公式进行拟合
我们观察三维点图，发现在X（Slip_angle）方向满足二维的公式（即下图），在Y（FZ）方向满足一个一次方程z=ky，所以综合写入方程：z=Dyysin(Cyatan(Byx-Ey(Byx-atan(Byx))))+Sv
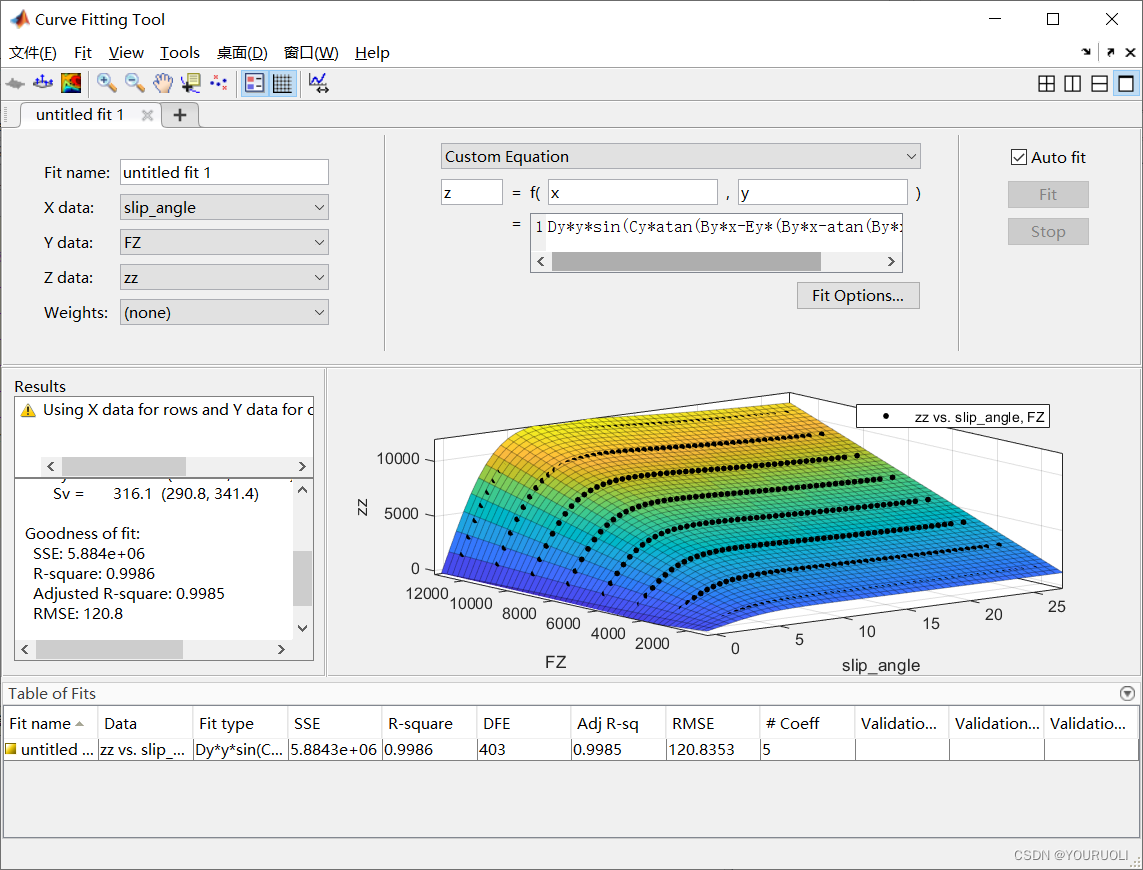
在这里插入图片描述
准确度R²=0.9986
拟合结果如下：

	   By =      0.1915  (0.188, 0.195)Cy =       1.396  (1.378, 1.414)Dy =      0.8896  (0.8857, 0.8934)Ey =     -0.6462  (-0.8374, -0.4551)Sv =       316.1  (290.8, 341.4)

这篇关于Matlab拟合工具箱拟合轮胎侧偏刚度的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！