TensorFlow学习－－学习率衰减/learning rate decay

2023-10-21 22:50
文章标签 学习 learning tensorflow 衰减 rate decay

本文主要是介绍TensorFlow学习－－学习率衰减/learning rate decay，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

学习率衰减

学习率衰减（learning rate decay）
在训练神经网络时，使用学习率控制参数的更新速度．学习率较小时，会大大降低参数的更新速度；学习率较大时，会使搜索过程中发生震荡，导致参数在极优值附近徘徊．
为此，在训练过程中引入学习率衰减，使学习率随着训练的进行逐渐衰减．

TensorFlow中实现的学习率衰减方法：

  • tf.train.piecewise_constant　分段常数衰减
  • tf.train.inverse_time_decay　反时限衰减
  • tf.train.polynomial_decay　多项式衰减
  • tf.train.exponential_decay　指数衰减
  • tf.train.natural_exp_decay　自然指数衰减
  • tf.train.cosine_decay　余弦衰减
  • tf.train.linear_cosine_decay　线性余弦衰减
  • tf.train.noisy_linear_cosine_decay　噪声线性余弦衰减
    函数返回衰减的学习率．

分段常数衰减

tf.train.piecewise_constant()　指定间隔的分段常数．
参数：

  • x：0-D标量Tensor．
  • boundaries：边界，tensor或list.
  • values：指定定义区间的值．
  • name：操作的名称，默认为PiecewiseConstant．

分段常数衰减就是在定义好的区间上，分别设置不同的常数值，作为学习率的初始值和后续衰减的取值．

示例：

#!/usr/bin/python
# coding:utf-8# piecewise_constant 阶梯式下降法
import matplotlib.pyplot as plt
import tensorflow as tf
global_step = tf.Variable(0, name='global_step', trainable=False)
boundaries = [10, 20, 30]
learing_rates = [0.1, 0.07, 0.025, 0.0125]
y = []
N = 40
with tf.Session() as sess:sess.run(tf.global_variables_initializer())for global_step in range(N):learing_rate = tf.train.piecewise_constant(global_step, boundaries=boundaries, values=learing_rates)lr = sess.run([learing_rate])y.append(lr[0])x = range(N)
plt.plot(x, y, 'r-', linewidth=2)
plt.title('piecewise_constant')
plt.show()

这里写图片描述

指数衰减

指数衰减

tf.train.exponential_decay()　应用指数衰减的学习率．
指数衰减是最常用的衰减方法．
参数：

  • learning_rate：初始学习率．
  • global_step：用于衰减计算的全局步数，非负．用于逐步计算衰减指数．
  • decay_steps：衰减步数，必须是正值．决定衰减周期．
  • decay_rate：衰减率．
  • staircase：若为True，则以不连续的间隔衰减学习速率即阶梯型衰减（就是在一段时间内或相同的eproch内保持相同的学习率）；若为False，则是标准指数型衰减．
  • name：操作的名称，默认为ExponentialDecay．（可选项）

指数衰减的学习速率计算公式为：

decayed_learning_rate = learning_rate * decay_rate ^ (global_step / decay_steps)

优点：简单直接，收敛速度快．

示例，阶梯型衰减与指数型衰减对比：

#!/usr/bin/python
# coding:utf-8
import matplotlib.pyplot as plt
import tensorflow as tf
global_step = tf.Variable(0, name='global_step', trainable=False)y = []
z = []
N = 200
with tf.Session() as sess:sess.run(tf.global_variables_initializer())for global_step in range(N):# 阶梯型衰减learing_rate1 = tf.train.exponential_decay(learning_rate=0.5, global_step=global_step, decay_steps=10, decay_rate=0.9, staircase=True)# 标准指数型衰减learing_rate2 = tf.train.exponential_decay(learning_rate=0.5, global_step=global_step, decay_steps=10, decay_rate=0.9, staircase=False)lr1 = sess.run([learing_rate1])lr2 = sess.run([learing_rate2])y.append(lr1[0])z.append(lr2[0])x = range(N)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.set_ylim([0, 0.55])
plt.plot(x, y, 'r-', linewidth=2)
plt.plot(x, z, 'g-', linewidth=2)
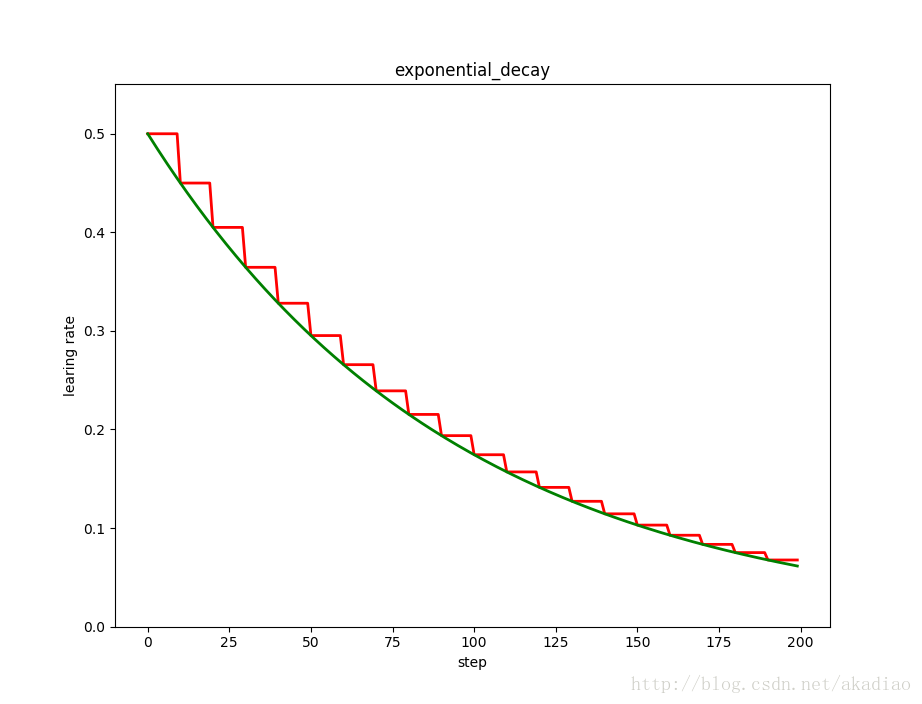
plt.title('exponential_decay')
ax.set_xlabel('step')
ax.set_ylabel('learing rate')
plt.show()

如图，红色：阶梯型；绿色：指数型：
这里写图片描述

自然指数衰减

tf.train.natural_exp_decay() 　应用自然指数衰减的学习率．
参数：

  • learning_rate：初始学习率．
  • global_step：用于衰减计算的全局步数，非负.
  • decay_steps：衰减步数．
  • decay_rate：衰减率．
  • staircase：若为True，则是离散的阶梯型衰减（就是在一段时间内或相同的eproch内保持相同的学习率）；若为False，则是标准型衰减．
  • name: 操作的名称，默认为ExponentialTimeDecay．

natural_exp_decay 和 exponential_decay 形式近似，natural_exp_decay的底数是e．自然指数衰减比指数衰减要快的多，一般用于较快收敛，容易训练的网络．
自然指数衰减的学习率计算公式为：

decayed_learning_rate = learning_rate * exp(-decay_rate * global_step)

示例，指数衰减与自然指数衰减的阶梯型与指数型：

#!/usr/bin/python
# coding:utf-8import matplotlib.pyplot as plt
import tensorflow as tf
global_step = tf.Variable(0, name='global_step', trainable=False)y = []
z = []
w = []
N = 200
with tf.Session() as sess:sess.run(tf.global_variables_initializer())for global_step in range(N):# 阶梯型衰减learing_rate1 = tf.train.natural_exp_decay(learning_rate=0.5, global_step=global_step, decay_steps=10, decay_rate=0.9, staircase=True)# 标准指数型衰减learing_rate2 = tf.train.natural_exp_decay(learning_rate=0.5, global_step=global_step, decay_steps=10, decay_rate=0.9, staircase=False)# 指数衰减learing_rate3 = tf.train.exponential_decay(learning_rate=0.5, global_step=global_step, decay_steps=10, decay_rate=0.9, staircase=False)lr1 = sess.run([learing_rate1])lr2 = sess.run([learing_rate2])lr3 = sess.run([learing_rate3])y.append(lr1[0])z.append(lr2[0])w.append(lr3[0])x = range(N)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.set_ylim([0, 0.55])
plt.plot(x, y, 'r-', linewidth=2)
plt.plot(x, z, 'g-', linewidth=2)
plt.plot(x, w, 'b-', linewidth=2)
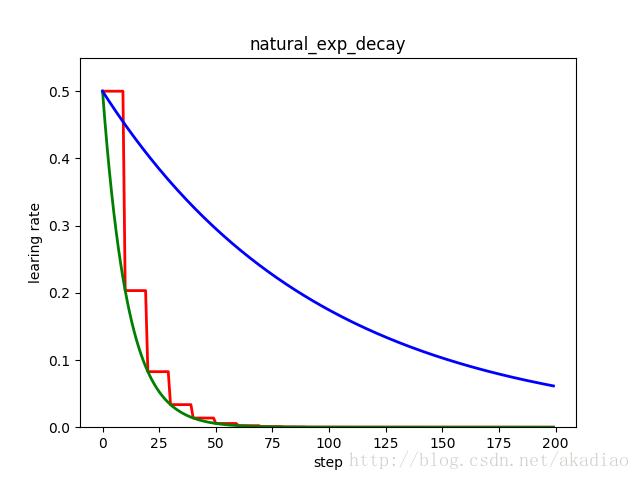
plt.title('natural_exp_decay')
ax.set_xlabel('step')
ax.set_ylabel('learing rate')
plt.show()

如图，红色：阶梯型；绿色：指数型；蓝色指数型衰减：
这里写图片描述

多项式衰减

tf.train.polynomial_decay()　应用多项式衰减的学习率．
参数：

  • learning_rate：初始学习率．
  • global_step：用于衰减计算的全局步数，非负.
  • decay_steps：衰减步数，必须是正值．
  • end_learning_rate：最低的最终学习率．
  • power：多项式的幂，默认为1.0（线性）．
  • cycle：学习率下降后是否重新上升．
  • name：操作的名称，默认为PolynomialDecay。

函数使用多项式衰减，以给定的decay_steps将初始学习率（learning_rate）衰减至指定的学习率（end_learning_rate）．

多项式衰减的学习率计算公式为：

global_step = min(global_step,decay_steps)
decayed_learning_rate = (learning_rate-end_learning_rate)*(1-global_step/decay_steps)^ (power)+end_learning_rate

参数cycle决定学习率是否在下降后重新上升．若cycle为True，则学习率下降后重新上升；使用decay_steps的倍数，取第一个大于global_steps的结果．

decay_steps = decay_steps*ceil(global_step/decay_steps)
decayed_learning_rate = (learning_rate-end_learning_rate)*(1-global_step/decay_steps)^ (power)+end_learning_rate

参数cycle目的：防止神经网络训练后期学习率过小导致网络一直在某个局部最小值中振荡；这样，通过增大学习率可以跳出局部极小值．

示例，学习率下降后是否重新上升对比：

#!/usr/bin/python
# coding:utf-8
# 学习率下降后是否重新上升
import matplotlib.pyplot as plt
import tensorflow as tf
y = []
z = []
N = 200
global_step = tf.Variable(0, name='global_step', trainable=False)with tf.Session() as sess:sess.run(tf.global_variables_initializer())for global_step in range(N):# cycle=Falselearing_rate1 = tf.train.polynomial_decay(learning_rate=0.1, global_step=global_step, decay_steps=50,end_learning_rate=0.01, power=0.5, cycle=False)# cycle=Truelearing_rate2 = tf.train.polynomial_decay(learning_rate=0.1, global_step=global_step, decay_steps=50,end_learning_rate=0.01, power=0.5, cycle=True)lr1 = sess.run([learing_rate1])lr2 = sess.run([learing_rate2])y.append(lr1[0])z.append(lr2[0])x = range(N)
fig = plt.figure()
ax = fig.add_subplot(111)
plt.plot(x, z, 'g-', linewidth=2)
plt.plot(x, y, 'r--', linewidth=2)
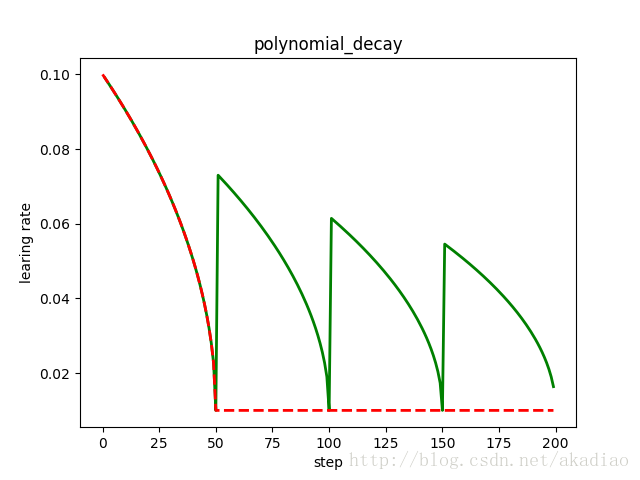
plt.title('polynomial_decay')
ax.set_xlabel('step')
ax.set_ylabel('learing rate')
plt.show()

如图，红色：下降后不再上升；绿色：下降后重新上升：
这里写图片描述

余弦衰减

余弦衰减

tf.train.cosine_decay()　将余弦衰减应用于学习率
参数：

  • learning_rate：标初始学习率．
  • global_step：用于衰减计算的全局步数.
  • decay_steps：衰减步数．
  • alpha：最小学习率（learning_rate的部分）。
  • name：操作的名称，默认为CosineDecay．

根据论文SGDR: Stochastic Gradient Descent with Warm Restarts提出．

余弦衰减的学习率计算公式为：

global_step = min(global_step, decay_steps)
cosine_decay = 0.5 * (1 + cos(pi * global_step / decay_steps))
decayed = (1 - alpha) * cosine_decay + alpha
decayed_learning_rate = learning_rate * decayed
线性余弦衰减

tf.train.linear_cosine_decay()　将线性余弦衰减应用于学习率．
参数：

  • learning_rate：标初始学习率．
  • global_step：用于衰减计算的全局步数.
  • decay_steps：衰减步数。
  • num_periods：衰减余弦部分的周期数．
  • alpha：见计算．
  • beta：见计算．
  • name：操作的名称，默认为LinearCosineDecay。

根据论文Neural Optimizer Search with Reinforcement Learning提出．

线性余弦衰减的学习率计算公式为：

global_step=min(global_step,decay_steps)
linear_decay=(decay_steps-global_step)/decay_steps)
cosine_decay = 0.5*(1+cos(pi*2*num_periods*global_step/decay_steps))
decayed=(alpha+linear_decay)*cosine_decay+beta
decayed_learning_rate=learning_rate*decayed
噪声线性余弦衰减

tf.train.noisy_linear_cosine_decay()　将噪声线性余弦衰减应用于学习率．
参数：

  • learning_rate：标初始学习率．
  • global_step：用于衰减计算的全局步数.
  • decay_steps：衰减步数．
  • initial_variance：噪声的初始方差．
  • variance_decay：衰减噪声的方差．
  • num_periods：衰减余弦部分的周期数．
  • alpha：见计算．
  • beta：见计算．
  • name：操作的名称，默认为NoisyLinearCosineDecay．

根据论文Neural Optimizer Search with Reinforcement Learning提出．在衰减过程中加入了噪声，一定程度上增加了线性余弦衰减的随机性和可能性．

噪声线性余弦衰减的学习率计算公式为：

global_step=min(global_step,decay_steps)
linear_decay=(decay_steps-global_step)/decay_steps)
cosine_decay=0.5*(1+cos(pi*2*num_periods*global_step/decay_steps))
decayed=(alpha+linear_decay+eps_t)*cosine_decay+beta
decayed_learning_rate =learning_rate*decayed

示例，线性余弦衰减与噪声线性余弦衰减：

#!/usr/bin/python
# coding:utf-8
import matplotlib.pyplot as plt
import tensorflow as tf
y = []
z = []
w = []
N = 200
global_step = tf.Variable(0, name='global_step', trainable=False)with tf.Session() as sess:sess.run(tf.global_variables_initializer())for global_step in range(N):# 余弦衰减learing_rate1 = tf.train.cosine_decay(learning_rate=0.1, global_step=global_step, decay_steps=50,alpha=0.5)# 线性余弦衰减learing_rate2 = tf.train.linear_cosine_decay(learning_rate=0.1, global_step=global_step, decay_steps=50,num_periods=0.2, alpha=0.5, beta=0.2)# 噪声线性余弦衰减learing_rate3 = tf.train.noisy_linear_cosine_decay(learning_rate=0.1, global_step=global_step, decay_steps=50,initial_variance=0.01, variance_decay=0.1, num_periods=0.2, alpha=0.5, beta=0.2)lr1 = sess.run([learing_rate1])lr2 = sess.run([learing_rate2])lr3 = sess.run([learing_rate3])y.append(lr1[0])z.append(lr2[0])w.append(lr3[0])x = range(N)
fig = plt.figure()
ax = fig.add_subplot(111)
plt.plot(x, z, 'b-', linewidth=2)
plt.plot(x, y, 'r-', linewidth=2)
plt.plot(x, w, 'g-', linewidth=2)
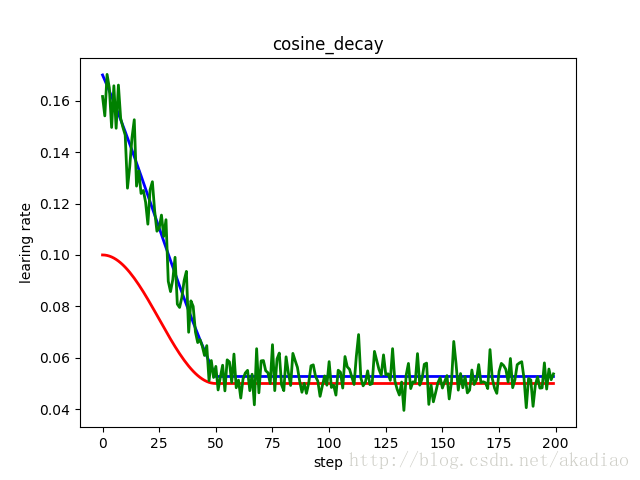
plt.title('cosine_decay')
ax.set_xlabel('step')
ax.set_ylabel('learing rate')
plt.show()

如图，红色：余弦衰减；蓝色：线性余弦衰减；绿色：噪声线性余弦衰减；
这里写图片描述

反时限衰减

tf.train.inverse_time_decay()　将反时限衰减应用到初始学习率．
参数：

  • learning_rate：初始学习率．
  • global_step：用于衰减计算的全局步数．
  • decay_steps：衰减步数．
  • decay_rate：衰减率．
  • staircase：是否应用离散阶梯型衰减．（否则为连续型）
  • name：操作的名称，默认为InverseTimeDecay．

该函数应用反向衰减函数提供初始学习速率．利用global_step来计算衰减的学习速率．计算公式为：

decayed_learning_rate =learning_rate/(1+decay_rate* global_step/decay_step)

若staircase为True时：

decayed_learning_rate =learning_rate/(1+decay_rate*floor(global_step/decay_step))

示例，反时限衰减的阶梯型衰减与连续型对比：

#!/usr/bin/python
# coding:utf-8import matplotlib.pyplot as plt
import tensorflow as tf
y = []
z = []
N = 200
global_step = tf.Variable(0, name='global_step', trainable=False)with tf.Session() as sess:sess.run(tf.global_variables_initializer())for global_step in range(N):# 阶梯型衰减learing_rate1 = tf.train.inverse_time_decay(learning_rate=0.1, global_step=global_step, decay_steps=20,decay_rate=0.2, staircase=True)# 连续型衰减learing_rate2 = tf.train.inverse_time_decay(learning_rate=0.1, global_step=global_step, decay_steps=20,decay_rate=0.2, staircase=False)lr1 = sess.run([learing_rate1])lr2 = sess.run([learing_rate2])y.append(lr1[0])z.append(lr2[0])x = range(N)
fig = plt.figure()
ax = fig.add_subplot(111)
plt.plot(x, z, 'r-', linewidth=2)
plt.plot(x, y, 'g-', linewidth=2)
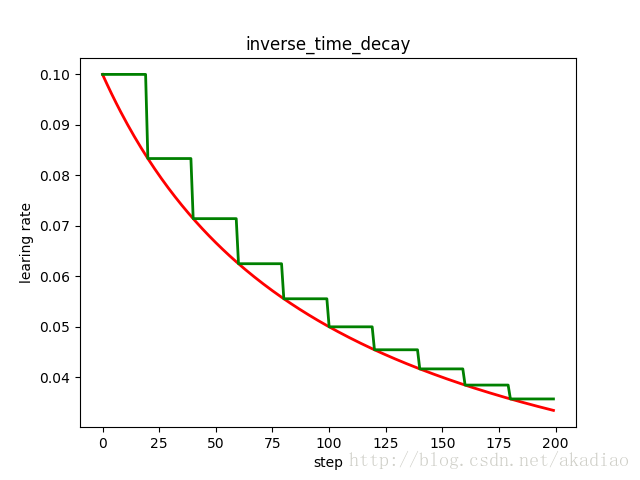
plt.title('inverse_time_decay')
ax.set_xlabel('step')
ax.set_ylabel('learing rate')
plt.show()

如图，蓝色：阶梯型；红色：连续型：
这里写图片描述

参考：
tensorflow　APIr1.6

这篇关于TensorFlow学习－－学习率衰减/learning rate decay的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/257486。

相关文章

51单片机学习记录———定时器

51单片机学习记录———定时器

文章目录 前言一、定时器介绍二、STC89C52定时器资源三、定时器框图四、定时器模式五、定时器相关寄存器六、定时器练习 前言 一个学习嵌入式的小白~ 有问题评论区或私信指出~ 提示：以下是本篇文章正文内容，下面案例可供参考 一、定时器介绍 定时器介绍：51单片机的定时器属于单片机的内部资源，其电路的连接和运转均在单片机内部完成。 定时器作用： 1.用于计数系统，可
阅读更多...
问题：第一次世界大战的起止时间是 #其他#学习方法#微信

问题：第一次世界大战的起止时间是 #其他#学习方法#微信

问题：第一次世界大战的起止时间是 A.1913 ~1918 年 B.1913 ~1918 年 C.1914 ~1918 年 D.1914 ~1919 年 参考答案如图所示
阅读更多...
[word] word设置上标快捷键 #学习方法#其他#媒体

[word] word设置上标快捷键 #学习方法#其他#媒体

word设置上标快捷键 办公中，少不了使用word，这个是大家必备的软件，今天给大家分享word设置上标快捷键，希望在办公中能帮到您！ 1、添加上标 在录入一些公式，或者是化学产品时，需要添加上标内容，按下快捷键Ctrl+shift++就能将需要的内容设置为上标符号。 word设置上标快捷键的方法就是以上内容了，需要的小伙伴都可以试一试呢！
阅读更多...
AssetBundle学习笔记

AssetBundle学习笔记

AssetBundle是unity自定义的资源格式，通过调用引擎的资源打包接口对资源进行打包成.assetbundle格式的资源包。本文介绍了AssetBundle的生成，使用，加载，卸载以及Unity资源更新的一个基本步骤。 目录 1.定义： 2.AssetBundle的生成： 1）设置AssetBundle包的属性——通过编辑器界面 补充：分组策略 2）调用引擎接口API
阅读更多...
Javascript高级程序设计(第四版)--学习记录之变量、内存

Javascript高级程序设计(第四版)--学习记录之变量、内存

原始值与引用值 原始值：简单的数据即基础数据类型，按值访问。 引用值：由多个值构成的对象即复杂数据类型，按引用访问。 动态属性 对于引用值而言，可以随时添加、修改和删除其属性和方法。 let person = new Object();person.name = 'Jason';person.age = 42;console.log(person.name,person.age);//'J
阅读更多...
大学湖北中医药大学法医学试题及答案，分享几个实用搜题和学习工具 #微信#学习方法#职场发展

大学湖北中医药大学法医学试题及答案，分享几个实用搜题和学习工具 #微信#学习方法#职场发展

今天分享拥有拍照搜题、文字搜题、语音搜题、多重搜题等搜题模式，可以快速查找问题解析，加深对题目答案的理解。 1.快练题 这是一个网站 找题的网站海量题库,在线搜题,快速刷题~为您提供百万优质题库,直接搜索题库名称,支持多种刷题模式:顺序练习、语音听题、本地搜题、顺序阅读、模拟考试、组卷考试、赶快下载吧! 2.彩虹搜题 这是个老公众号了 支持手写输入，截图搜题，详细步骤，解题必备
阅读更多...
《offer来了》第二章学习笔记

《offer来了》第二章学习笔记

1.集合 Java四种集合：List、Queue、Set和Map 1.1.List：可重复 有序的Collection ArrayList： 基于数组实现，增删慢，查询快，线程不安全 Vector： 基于数组实现，增删慢，查询快，线程安全 LinkedList： 基于双向链实现，增删快，查询慢，线程不安全 1.2.Queue：队列 ArrayBlockingQueue：
阅读更多...
硬件基础知识——自学习梳理

硬件基础知识——自学习梳理

计算机存储分为闪存和永久性存储。 硬盘（永久存储）主要分为机械磁盘和固态硬盘。 机械磁盘主要靠磁颗粒的正负极方向来存储0或1，且机械磁盘没有使用寿命。 固态硬盘就有使用寿命了，大概支持30w次的读写操作。 闪存使用的是电容进行存储，断电数据就没了。 器件之间传输bit数据在总线上是一个一个传输的，因为通过电压传输（电流不稳定），但是电压属于电势能，所以可以叠加互相干扰，这也就是硬盘，U盘
阅读更多...
人工智能机器学习算法总结神经网络算法(前向及反向传播)

人工智能机器学习算法总结神经网络算法(前向及反向传播)

1.定义，意义和优缺点 定义: 神经网络算法是一种模仿人类大脑神经元之间连接方式的机器学习算法。通过多层神经元的组合和激活函数的非线性转换，神经网络能够学习数据的特征和模式，实现对复杂数据的建模和预测。(我们可以借助人类的神经元模型来更好的帮助我们理解该算法的本质，不过这里需要说明的是，虽然名字是神经网络，并且结构等等也是借鉴了神经网络，但其原型以及算法本质上还和生物层面的神经网络运行原理存在
阅读更多...
Python应用开发——30天学习Streamlit Python包进行APP的构建（9）

Python应用开发——30天学习Streamlit Python包进行APP的构建（9）

st.area_chart 显示区域图。 这是围绕 st.altair_chart 的语法糖。主要区别在于该命令使用数据自身的列和指数来计算图表的 Altair 规格。因此，在许多 "只需绘制此图 "的情况下，该命令更易于使用，但可定制性较差。 如果 st.area_chart 无法正确猜测数据规格，请尝试使用 st.altair_chart 指定所需的图表。 Function signa
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2