本文主要是介绍SystemVerilog Assertions应用指南 Chapter 1.21重复运算符,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1.21重复运算符
如果信号“stat”在任何给定的时钟上升沿跳变为高,接着从下一个时钟周期起,信号“a”保持三个连续时钟周期为高,然后下一个时钟周期,信号“stop”为高,像上述描述的序列可以使用下面的SVA代码来检验。
sequence ss ;@(posedge clk) $rose(start) |-> ##1 a ##1 a ##1 a ##1 stop;
endsequence 如果信号“a”需要在很多个周期中保持高电平,编写这样个检验器可能会非常冗长。而且这个例子要求信号“a”连续地保持高电平。当我们只希望检查信号“a”是否在被检测时保持为高,而不一定是三个连续的时钟周期的时候,协议就会变得复杂起来。换句话说,信号“a”需要连续地或者间歇地重复自己三次。
SVA语言提供三种不同的重复运算符:连续重复( consecutiverepetition),跟随重复( go to repetition),非连续重复( non -consecutiverepetition)。
连续重复允许用户表明信号或者序列将在指定数量的时钟周期内都连续地匹配。信号的每次匹配之间都有一个时钟周期的隐藏延迟。连续重复运算符的基本语法如下所示。
signal or sequence [*n]“n”是表达式应该匹配的次数。比如,a[*3]可以被展开成下面的式子。
a ##1 a ##1 a而序列(a ##1 b) [*3]可以展开为
(a ##1 b) ##1 (a ##1 b ) ##1 (a ##1 b)跟随重复——允许用户表明一个表达式将匹配达到指定的次数,而且不一定在连续的时钟周期上发生。这些匹配可以是间歇的。跟随重复的主要要求是被检验重复的表达式的最后一个匹配应该发生在整个序列匹配结束之前。跟随重复运算符的基本语法如下所示。
signal [->n]参考下面的序列:
start ##1 a[->3] ##1 stop 这个序列需要信号“a”的匹配(即信号“a”的第三次,也就是最后一次重复的匹配)正好发生在“stop”成功之前。换句话说,信号“stop”在序列的最后一个时钟周期匹配,而且在前一个时钟周期,信号“a”有一次匹配。
非连续重复—与跟随重复相似,除了它并不要求信号的最后一次重复匹配发生在整个序列匹配前的那个时钟周期。非连续重复运算符的基本语法如下所示。
signa1 [=n]在跟随重复和非连续重复中只允许使用表达式,不能使用序列。
1.21.1连续重复运算符[*]
属性p21检査在检验有效地开始两个时钟周期后,信号“a在连续的三个时钟周期为高,再过两个时钟周期,信号“stop”为高。下一个时钟周期,信号“stop”为低。
property p21;@(posedge clk) $rose(start) |-> ##2 (a[*3]) ##2 stop ##1 !stop;
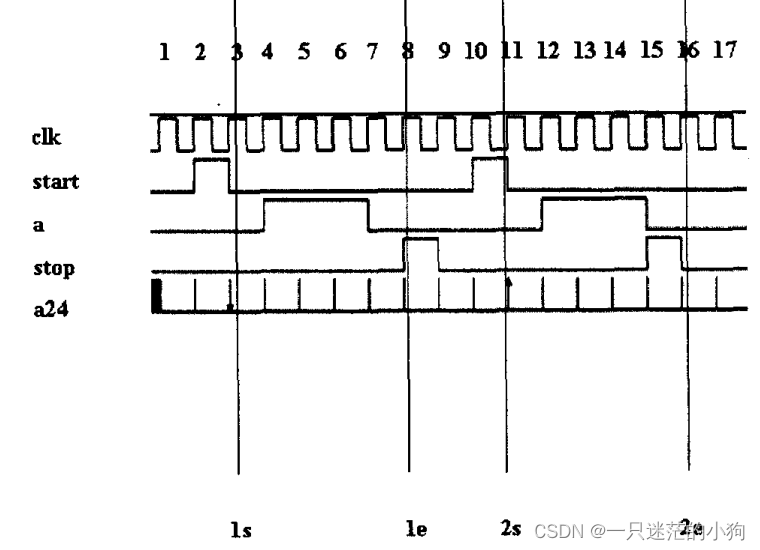
endpropertya21: assert property(p21); 图1-23显示了属性p21在模拟中的响应。波形中显示了2个失败和1个真正的成功。其他成功都是空成功。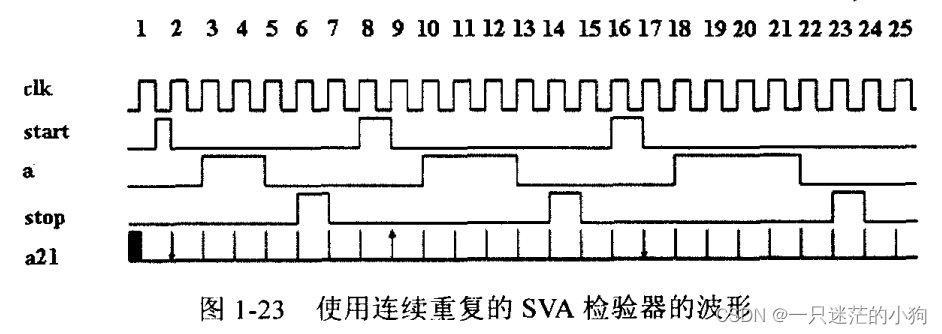
断言失败于时钟周期2—时钟周期2有一个有效的开始信号。检验器接着检验信号“a”是否从时钟周期4的上升沿开始有连续三个时钟周期为高。信号“a”在时钟周期4和5为高,但是在时钟周期6为低。因此检验失败。检査从时钟周期2开始,在时钟周期6失败。
断言成功于时钟周期9——在时钟周期9检测到一个有效的开始。于是检验器检查信号“a”是否在时钟周期11开始的3个连续时钟周期都为高。信号“a”在时钟周期11、12、13都像预期的那样被检测为高。两个时钟周期后(时钟周期15),信号“stop”如预期地为高。一个时钟周期以后,“stop”被检测为低。至此检验成功。注意,检査从时钟周期9开始,结束于时钟周期16。
断言失败于时钟周期17——在时钟周期17检测到一个有效的开始。于是检验器检查信号“a”是否在时钟周期19开始的3个连续时钟周期都为高。信号“a”在时钟周期19、20、21都像预期的那样为高。接着检验器检查信号“stp”在时钟周期23是否为高,但是没检测到。因此检验失败。可以看到,信号“a”保持了4个时钟周期的高电平。但是检验器只需要检查3个重复,因此直接继续检査信号“stop”。整个检査从时钟周期19开始,失败于时钟周期23。
1.21.2用于序列的连续重复运算符[*]
属性p22检查有效开始的两个时钟周期以后,序列(a#2b)重复三次,接着再过两个时钟周期,信号“stop”为高。
property p22;@(posedge clk) $rose(start) -> ##2 ((a ##2 b)[*3])##2 stop;
endpropertya22 :assert property(p22); 图1-24显示了属性p22在模拟中的响应。图中共显示了2个失败和1个真正的成功。
失败1—第一个失败由标记 1s 标出。有效的开始在这个点被检测到。两个时钟周期后,检验器期望序列(a##2 b)重复3次。但是序列只重复了两次。因此检验器失败,失败点由标记1e标出。
成功1—唯一一个真正的成功由标记2s标出。有效的开始在这个点被检测到。两个时钟周期后,检验器开始检查序列(a##2 b)是否重复3次。序列如预期地重复了3次。在序列重复被检验后,再过两个时钟周期,信号“stop”也如期望地为高。因此检验器成功,成功点由标记2e标出。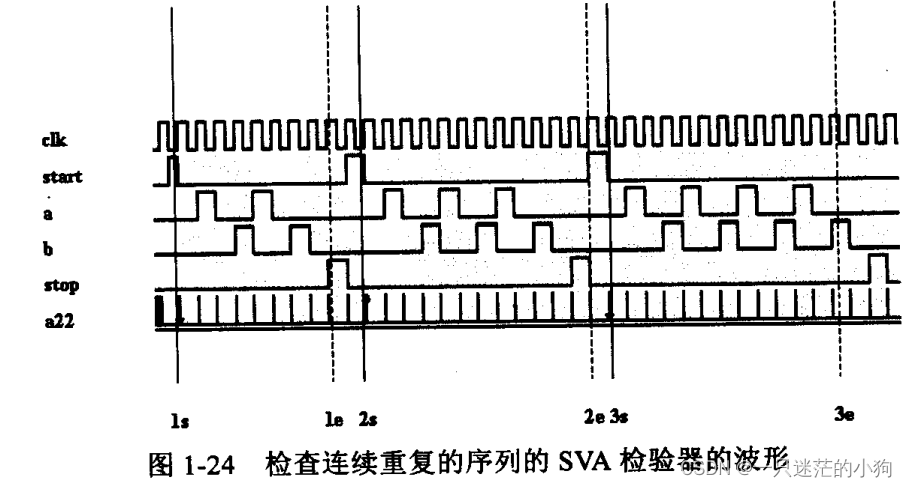
失败2—第二个失败由标记3s标出。有效的开始在这个点被检测到。两个时钟周期后,检验器开始检查序列(a##2b)是否重复3次。序列如预期地重复了3次。当序列重复被检验到后,信号“stop”被期望在两个时钟周期后为高,但是失败了。因此检验器失败,失败点由标记3e标出。
1.21.3用于带延迟窗口的序列的连续重复运算符[ * ]
属性p23检查在有效开始的两个时钟周期后,序列(a ##[1 : 4] b)重复3次,接着再过两个时钟周期,信号“stop”为高。实际上,这个序列有一个时序窗口,使得情况变得有些复杂。
property p23;@(posedge clk) $rose (start) |-> ##2 ((a ##[1 :4] b)[*3]) ##2 stop;
endpropertya23: assert property(p23);主序列(a ## [1:4] b)*3]可以被扩展成
((a##1b)or(a##2b)or(a##3b)or(a##4b))##1
((a#1b)or(a##2b)or(a#3b)or(a##4b))##1
((a ##1 b)or (a ##2 b)or(a ##3 b)or (a ##4 b)) 图1-25显示了属性p23在模拟中的响应。 图中有2个失败和1个真正的成功。
失败1—第一个失败由标记ls标出。这一点有个有效的开始。从这一点开始两个时钟周期后,检验器期望序列(a#爿4]b)重复3次。但是序列只重复了2次。因此检验器失败,失败点由标记le标出。可以看到成功的两个重复分别是(a ##1 b)和(a ##2 b)。
成功1——唯一的真正成功由标记2s标出。这一点有一个有效的开始。从这一点开始两个时钟周期后,检验器期望序列(a ## [1:4] b)重复3次。序列如预期地重复了3次。在成功重复之后,信号“stop”如期望地在两个时钟周期后为高。因此检验器成功了成功点由标记2e标出。可以看到成功的三个重复分别是(a ## 2 b),(a ## 4 b)和(a ## 2 b)。
失败2——第二个失败由标记3s标出。这一点有一个有效的开始。从这一点开始两个时钟周期后,检验器期望序列(a ## [1:4] b)重复3次。序列如预期地重复了3次。在成功地重复之后,信号“stop”被期望地在两个时钟周期后为高,但是失败了。因此检验器失败,失败点由标记3e标出。可以看到成功的三个重复分别是(a ## 2 b),(a ## 2 b)和(a ## 3 b)
1.21.4连续运算符[ * ]和可能性运算符
属性p23指定了一个重复序列的时序窗口。同样的,重复的次数也可以是一个窗口。比如,a[*1:5]表示信号“a”从某个时钟周期开始重复1~5次。这个定义可以展开成下面的表达式。
a or
(a ##1 a ) or
(a ##1 a ##1 a ) or
(a ##1 a ##1 a ##1 a) or
(a ##1 a ##1 a ##1 a ##1 a ) or 重复窗口的边界规则与延迟窗口的相同。左边的值必须小于右边的值。右边的值可以是符号“$”,这表示没有重复次数的限制。
属性p24显示了一个带没有重复次数限制的有限的检查。它检验有效开始两个时钟周期后,信号“a”将保持为高,直到信号“stop”跳变为高。
property p24;@(posedge clk) $rose(start) |->##2 (a[*1:$]) ##1 stop;
endpropertya24: assert property(p24); 图1-26显示了属性p24在模拟中的响应。图中有1个失败和1个真正的成功。
失败——1个有效的开始发生在时钟周期3,如标记ls所示。检查期望在两个时钟周期后,信号“a"”将保持为高直到信号“stop”有效。信号“a”一直为高直到时钟周期7。在时钟周期8,“a”被检测为低,但是信号“stop”仍然不为高。因此检验在时钟周期8失败,如标记le所示。
成功——1个有效的开始发生在时钟周期11,如标记1s所示。检查期望在两个时钟周期后,信号“a”将保持为高直到信号"stop”有效。信号“a”一直为高直到时钟周期15。在时钟周期,“a”被检测为低,但是信号“stop”如期望地为高。因此检验在时钟周期16成功,如标记2e所示。
图1-26使用连续重复和可能性运算符的SⅤA检验器的波形
1.21.5跟随重复运算符[->]
属性p25检查如果在任何时钟上升沿有有效的开始,两个时钟周期后,信号“a”连续或者间断地出现3次为高,接着信号“stop在下一个时钟周期为高。
property p25;@(posedge clk) $rose(start) |->##2 (a[->3]) ##1 stop;
endpropertya25: assert property(p25); 图1-27显示了属性p25在模拟中的响应。图中显示共有1个失败、1个成功和一个未完成的检查。
失败1—标记ls标出了检验器的一个有效开始。检验器期望在有效开始的两个时钟周期后,信号“a”重复3次。信号如预期地重复3次,在信号“a”的第3次匹配后,信号“stop”没能如期望的那样在下一个时钟周期为高。因此检查在标记1e所示位置失败了。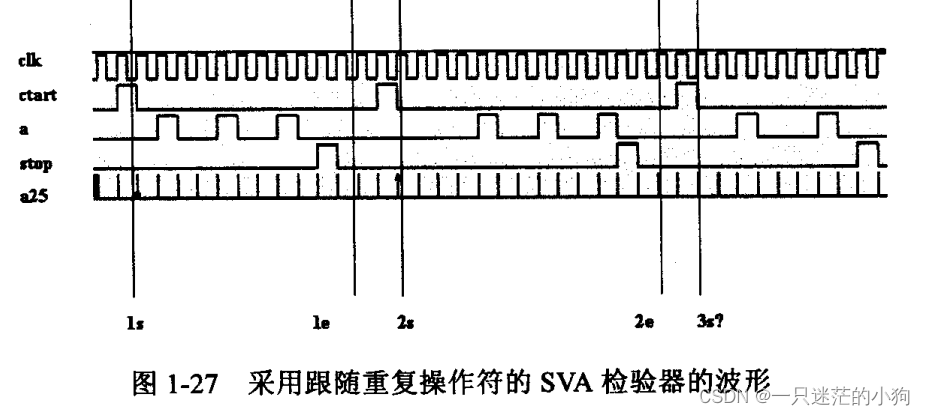
成功1—标记2s标出了检验器的一个有效开始。检验器期望在有效开始的两个时钟周期,信号“a”将重复3次。信号如预期地重复3次。在信号“a”的第3次匹配后,在下一个时钟周期信号“stop”如期望的那样为高。因此检查在标记2e所示位置成功了。
未完成1—一标记3s标出了检验器的一个有效开始。检验器期望在有效开始的两个时钟周期后,信号“a”重复3次。信号重复了两次,模拟就结束了。应注意到,在模拟周期结束前,信号“stop”出现了一次有效。由于重复语句还没有完成,这个有效的“stop”并没有发生任何作用。检验3个重复的语句阻塞了信号“stop”的检验。因此在模拟结束时这个检査未能完成。
1.21.6非连续重复运算符[=]
属性p26检查如果在任何时钟上升沿有有效的开始信号,两个时钟周期后,在一个有效的“stop”信号前,信号“a”连续或者间断地出现3次为高,然后一个时钟周期后“stop”应该为低。p26和p25做的是相同的检查,唯一的不同是p26使用的是非连续(non- consecutive)重复运算符而不是跟随(goto)重复运算符。这表示在属性p26中,在信号“stop”有效匹配的前一个时钟周期,信号“a”不一定需要有有效的匹配。
property p26;@(posedge clk) $rose(start) |-> ##2 (a[=3]) ##1 stop ##1 !stop;
endpropertya26: assert property(p26); 图1-28显示了属性p26在模拟中的响应。图中显示有2个真正的成功和1个未完成的检查。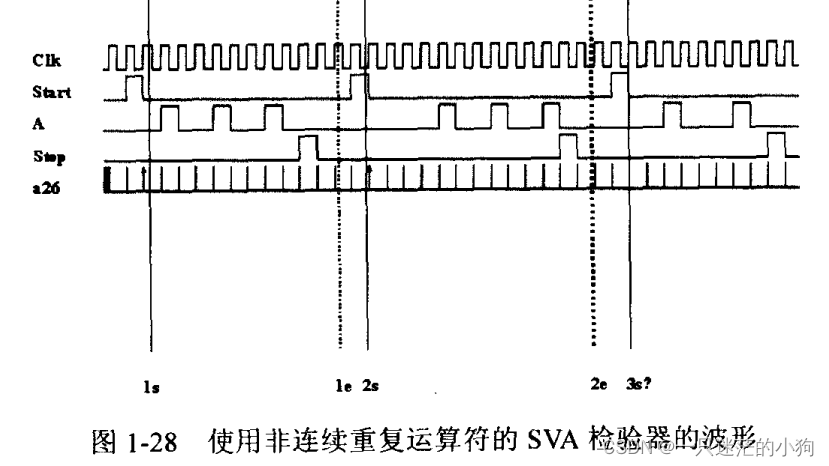
成功1——标记ls标出了检验器的一个有效开始。检验器期望在有效开始的两个时钟周期后,信号“a”重复3次。信号“a”如预期地重复3次,在“a”的第个匹配后,期望一个有效的信号“stop”,但是不必在下一个时钟周期发生。实际上,在信号“a”的第三次匹配的两个时钟周期后有一个有效的信号“stop”,因此检验如标记le所示的成功了。这就是跟随重复和非连续重复的不同之处。在相同情况下,属性p25由于使用的是跟随重复而失败了。
成功2——标记2s标出了检验器的一个有效开始。检验器期望在有效开始的两个时钟周期后,信号“a”重复3次。信号“a”如预期地重复3次,在“a”的第三次匹配后,期望一个有效的信号“stop”,但不必在下一个时钟周期发生。实际上,在信号的第三次匹配的1个时钟周期后有一个有效的信号“stop”,因此检验如标记2e所示的成功了。
未完成1——标记3s标出了检验器的一个有效开始。检验器期望在有效开始的两个时钟周期后,信号“a”重复3次。实际上信号“a”重复了两次,在第3次重复出现前,模拟结束了。同样应注意,信号“stop”在模拟周期结束前曾经出现为高。因为重复语句还没有完成,所以这个“stop”并没有起到任何作用。信号“a”重复三次的语句阻塞了信号“stop”的检验。因此在模拟结束时检验未完成。这个行为与跟随重复(“ go to"repetition)相同。
这篇关于SystemVerilog Assertions应用指南 Chapter 1.21重复运算符的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!