本文主要是介绍【论文笔记】Leveraging Line-point Consistence to Preserve Structures for Wide Parallax Image Stitching,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
论文链接:https://openaccess.thecvf.com/content/CVPR2021/papers/Jia_Leveraging_Line-Point_Consistence_To_Preserve_Structures_for_Wide_Parallax_Image_CVPR_2021_paper.pdf
代码链接:https://github.com/dut-media-lab/Image-Stitching
摘要
生成具有自然结构的高质量拼接图像是计算机视觉中的一项具有挑战性的任务。在本文中,我们成功地保留了宽视差图像的局部和全局几何结构,同时减少了伪影和失真。投影不变量特征数用于匹配输入图像的共面局部子区域。这些匹配良好的子区域之间的单应性产生一致的线和点对,抑制重叠区域中的伪影。我们探索并将全局共线结构引入到一个目标函数中,以指定和平衡图像变形所需的特征,这可以在减轻失真的同时保留局部和全局结构。考虑到人类视觉对线性结构的敏感性,我们还开发了综合的拼接质量的综合测量方法,来量化点的共线性和匹配线对的差异。大量实验通过呈现清晰的纹理并在拼接图像中保留突出的自然结构,证明了所提出的方法优于最先进的方法。特别是,我们的方法不仅表现出较低的错误,而且在所有测试图像中的差异最小。
1.介绍
图像拼接,将多个图像组合成具有更宽视野的更大图像[25],广泛用于摄影测量[24]、机器人导航[6]和智能手机全景[29]。为最先进的技术生成高质量的拼接图像仍然具有挑战性,因为它们会遭受严重不愉快的影响,例如伪影和失真,尤其是对于宽视差图像。
特征匹配是对齐多个图像以产生无伪影拼接的关键,因为匹配的特征充当对齐的锚。 SIFT 特征 [23] 广泛用于许多传统的特征点检测和匹配方法 [4, 5, 30]。最近的一些工作还引入了线特征,以在点容易失配的大视差和/或低纹理的情况下获得稳健的匹配[11]。林等人。在目标函数中通过不同的权重利用点和线特征[16]。不幸的是,这些方法分别匹配点和线,因此当不可避免地发生不匹配时,局部周围区域可能会不一致且不均匀地拉伸或压缩,从而在拼接图像中呈现伪影。廖等人。采用RANSAC策略通过使用图像之间的单应性来细化点和线对[17]。值得注意的是,单应关系仅适用于同一投影平面内的点和线[12]。因此,那些对单应性但忽略共面约束的改进无法给出准确的匹配。如图1中前三行红色矩形所示,右侧放大的重叠区域显示了相框、时钟和计算机上的伪影。探索共面区域并细化相应的点和线匹配对是非常可取的。

图像拼接必须保留线性结构,同时减轻失真,因为人类视觉感知对这些结构非常敏感。 as-projective-as-possible (APAP) 方法采用局部约束的参数扭曲 [30],但会遭受严重的形状扭曲,尤其是在非重叠区域,如图 1 中第一行的蓝色矩形所示。保形半投影 (SPHP) [4] 和全局相似性先验 (GSP) [5] 具有相似的想法,可以为不同的图像区域调整不同的扭曲。测地线保留[13]和线结构保留[3]涉及共线性保留,但它们的图像调整大小以一张全景图像作为输入,已经包含正确的全局几何结构作为参考。最近,廖等人提出单视角扭曲(SPW)[17]来保护线性结构,同时抑制扭曲。这些方法可以很好地保留局部结构,但在同时维护局部和全局线性结构时无法解决冲突。全局共线结构可以是横跨图像主要部分的一条长线,例如图 1 中两个图片帧下方的长线,也可以是几个单独的共线线段。当前的线检测器 [26] 无法检测或连接这些长线。因此,通过设置适当的参数可以很好地保留局部形状,但在图 1 的第二行中全局线性结构变形。在第三行中,保留线性结构会导致局部形状严重失真。保留局部和全局共线结构仍然没有解决。
同时,现有评价拼接质量的指标还不够全面。这些指标包括匹配点之间的距离 [30] 和像素强度局部模式上的平均几何误差 (SSIM) [27] 只能量化点匹配的性能。它们都不能反映线性结构上点的对齐或匹配线段的共线性。定量评估图像拼接线性结构的保存也是一个悬而未决的问题。
本文利用线和点的一致性来保留线性结构,这些线性结构是图像拼接的基本几何形状。我们将输入图像划分为线邻域上的共面区域,并使用一系列反映线和点固有性质的几何不变量来匹配来自不同视图的区域。因此,这些共面区域之间的单应性可以准确地生成线和点的匹配。随后,设计了用于warp的线引导目标函数以保留局部和全局线性结构并抑制失真。图 1 中的第四行表明我们的方法显着提高了图像质量。此外,为了更全面地分析拼接图像的质量,提出了一种线条的定量评价方法。我们的贡献总结如下:
• 我们设计了一种新的匹配策略,通过使用射影不变量探索共面子区域来获得一致的点和线对。这种匹配遵循基本的共面要求用于单应性,以便它可以提供准确的预对齐,同时消除伪影和非均匀失真。
• 据我们所知,我们是第一个将全局共线结构合并为显着减轻非自然扭曲的约束。
• 我们提出了一个综合度量来量化图像拼接的线性结构的保存。
我们将提出的方法与最先进的具有挑战性的自然图像对进行比较,具有突出的线性结构,涵盖相机运动、场景和视野的变化。我们的方法可以产生视觉上吸引人的拼接,我们的点匹配平均 RMSE 比 SPW [17] 低 31%。同时,我们的方法最准确、最稳定,可以根据所提出的度量来保留线性结构。第 3、4 和 5 节分别阐述了我们的贡献。
2. 相关工作
本文提出了同时保留局部和全局结构的线引导图像拼接方法。因此,本节回顾了以前与扭曲相关的工作,以减少失真和具有线结构约束的扭曲。
传统的拼接方法通常为每个输入图像估计一个最优的全局变换。它们仅适用于理想的近平面场景,并且生成的图像通常会受到局部伪影和投影失真的影响 [2]。因此,一些方法试图使扭曲适应图像的不同区域。林等人[21]提出了一种平滑变化的仿射(SVA)变换,以实现更好的局部适应。李等人使用贝叶斯模型去除异常值和用于分析扭曲的薄板样条[14]。高等人将图像分为地平面和远平面,并提出双单应扭曲(DHW)[8]来减少失真。保形半投影(SPHP)扭曲[4]结合了重叠和非重叠区域的投影变换。 Adaptive as-natural-as-possible (AANAP) warps [18] 有类似的想法,将重叠区域的单应变换转换为整个图像。赫尔曼等人[9]引入多个配准以获取更高的准确性,而不是单个配准。李等人。提出了一种准单应性(QH)扭曲[15],它依赖于全局单应性,同时挤压非重叠区域。但是,它们不够灵活,无法减少视差较大的场景的失真。
为了获得更好的对齐和更少的失真,APAP [30] 微调全局单应性扭曲以适应位置相关的对齐。陈等人通过最小化由对齐、局部和全局相似性项组成的能量函数,提出了一种基于全局相似性先验 (GSP) 的扭曲 [5]。他们的方法旨在解决非重叠区域的失真,但线性结构没有得到很好的保护。张等人通过设置一系列先验约束和手动指导来获得更好的性能[32]。林等人考虑到像素强度的差异,这在低纹理图像中效果很好[20]。李等人将图像分割成超像素,并根据视差场景的翘曲残差使用计算出的特征匹配来自适应地翘曲它们[12]。
此外,还有一些基于接缝的方法可以减少局部失真。提出了一种容忍视差的扭曲,它结合了单应性和内容保留扭曲(CPW)[22]来控制失真[31]。然而,他们的方法仍然会导致大视差的形状失真。Lin 等人。通过自适应特征加权迭代地改进接缝引导的局部对齐,并引入了一个新术语来保留显着线结构方法[19]。然而,非重叠区域仍然存在全局失真。
为了实现更好的拼接质量,减少失真并保留线性结构,Li 等人将线特征引入图像拼接,通过引入线性对齐项[16]来改进内容保留扭曲。向等人提出了一种具有全局相似性约束的线引导局部扭曲[28]。廖等人同时强调单视角扭曲的不同特征,包括对齐、扭曲和显着性 [17]。然而,全局共线结构很少被解决,并且在这些方法中仍然存在局部和全局结构保持之间的冲突。
3. 基于点线约束一致性进行预对齐
在本节中,设计了一种基于双特征(线和点)的预对齐算法,如图 2 所示。
- 首先,基于在线检测将图像划分为共面子区域,其中一个如图 2 所示 的绿色矩形。
- 然后,通过从一系列射影不变量计算的相似度来匹配子区域。
- 第三,增加和细化匹配点对,通过匹配区域之间的单应性匹配线。
- 最后,基于双重特征构建全局预对齐。
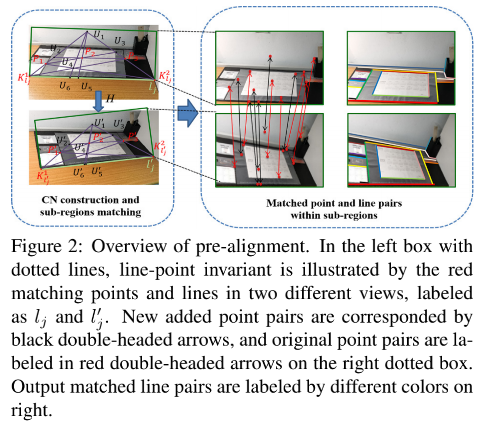
3.1 基于线检测的子区域划分
共面区域之间的局部单应性比全局单应性更准确。 由于多条线是由平面相交形成的,我们粗略假设,由线长确定的邻域可以看作是图像的局部共面子区域。利用LSD[26]得到原图线段,然后根据梯度方向将线的邻域分为左侧和右侧,因为位于线不同侧的点可能不共面。 一条线的梯度定义为它上面所有点的平均梯度。 如图 3 所示,在一条直线的附近,任何一个像素点到直线的距离都小于 α·len(l),并且到垂直平分线的距离小于 β·len(l)。 在我们的实验中,α 和 β 分别设置为 2.0 和 0.5 [10]。

3.2 基于点线不变性的子区域匹配
为了匹配共面的子区域,最终匹配更多的线点对,引入投射不变特征数(CN)来构造线-点不变量,并在此基础上定义子区域之间的相似度。 CN 定义如下:
令 K 为域, P m P^m Pm(K) 为 K 上的 m 维投影空间, { P i } i = 1 , 2 , . . . , R \{P_i\}_{i=1,2,...,R} {Pi}i=1,2,...,R 为 P m P^m Pm(K) 中构造闭环的不同点( P R + 1 = P 1 P_{R+1}=P_1 PR+1=P1)。 在线段 { P i P i + 1 } i = 1 , 2 , . . . , R \{P_iP_{i+1} \}_{i=1,2,...,R} {PiPi+1}i=1,2,...,R 上有不同的点 { Q ( j ) } i = 1 , 2 , . . . , S \{Q^{(j)}\}_{i=1,2,...,S} {Q(j)}i=1,2,...,S ,每个点 Q i ( j ) Q_i^{(j)} Qi(j) 可以由 P i P_i Pi 和 P i + 1 P_{i+1} Pi+1 线性表示为 Q i ( j ) = a i ( j ) P i + b i ( j ) P i + 1 Q_i^{(j)}=a_i^{(j)}P_i+b_i^{(j)}P_{i+1} Qi(j)=ai(j)Pi+bi(j)Pi+1。 令 P = { P i } i = 1 , 2 , . . . , R , Q = { Q i ( j ) } i = 1 , 2 , . . . , R j = 1 , 2 , . . . , S P=\{P_i\}_{i=1,2,...,R},Q=\{Q_i^{(j)}\}_{i=1,2,...,R}^{j=1,2,...,S} P={Pi}i=1,2,...,R,Q={Qi(j)}i=1,2,...,Rj=1,2,...,S,则该量称为 P 和 Q 的特征数

由于 CN 的构造需要一个闭环并且每条边上的点数相等,因此我们使用五个点来构造一个三角形,并且每条边上都有相等的交点 [10]。 如图2左上图所示, K l 1 K_l^1 Kl1 和 K l 2 K_l^2 Kl2 是红线 l 上的两个端点。 P 1 , P 2 , P 3 P_1, P_2, P_3 P1,P2,P3 是直线同一侧的三个非共线特征点,用红点标记。 任意三个点( K l 1 , K l 2 , P 1 , P 2 , P 3 K_l^1, K_l^2, P_1, P_2, P_3 Kl1,Kl2,P1,P2,P3)不共线。
我们用两个点 P i , P j P_i, P_j Pi,Pj 表示一条直线,即 P i P j ‾ \overline{P_iP_j} PiPj,然后两条直线 P i P j ‾ , P k P m ‾ \overline{P_iP_j}, \overline{P_kP_m} PiPj,PkPm 的交点表示为 < P i P j ‾ , P k P m ‾ > <\overline{P_iP_j}, \overline{P_kP_m}> <PiPj,PkPm>。我们可以获取几个相交点(蓝色点),包括 U 1 = < K l 1 P 1 ‾ , K l 2 P 3 ‾ > , U 2 = < K l 1 P 1 ‾ , P 2 P 3 ‾ > , U 3 = < P 1 P 2 ‾ , K l 2 P 3 ‾ > , U 4 = < K l 1 P 3 ‾ , P 1 K l 2 ‾ > , U 5 = < K l 1 K l 2 ‾ , U 1 P 2 ‾ > , U 6 = < K l 1 K l 2 ‾ , U 1 U 4 ‾ > U_1=<\overline{K^1_lP_1}, \overline{K_l^2P_3}>, U_2=<\overline{K^1_lP_1}, \overline{P_2P_3}>, U_3=<\overline{P_1P_2}, \overline{K_l^2P_3}>, U_4=<\overline{K^1_lP_3}, \overline{P_1K_l^2}>, U_5=<\overline{K^1_lK_l^2}, \overline{U_1P_2}>, U_6=<\overline{K^1_lK_l^2}, \overline{U_1U_4}> U1=<Kl1P1,Kl2P3>,U2=<Kl1P1,P2P3>,U3=<P1P2,Kl2P3>,U4=<Kl1P3,P1Kl2>,U5=<Kl1Kl2,U1P2>,U6=<Kl1Kl2,U1U4>.
因此,我们有 △ K l 1 U 1 K l 2 \triangle K_l^1U_1K_l^2 △Kl1U1Kl2,然后可以计算 P = { K l 2 , U 1 , K l 2 } , Q = { P 1 , U 2 , U 3 , P 3 , U 5 , U 6 } P=\{K_l^2,U_1, K_l^2\},Q=\{P_1, U_2, U_3, P_3, U_5, U_6\} P={Kl2,U1,Kl2},Q={P1,U2,U3,P3,U5,U6}的 CN。此后,在图2左下图所示的另一个视图中,我们可以用同样的方法构造 KaTeX parse error: Expected group after '^' at position 22: …gle K_l^{1'}U_1^̲'K_l^{2'}, C N ( l , P 1 , P 2 , P 3 ) CN(l, P_1, P_2,P_3) CN(l,P1,P2,P3)等于$CN(l’ , P’_1, P’_2,P’_3) $具有相应的匹配线和点对。 通过不同的特征点可以得到一系列的CN值。
令 I 和 I ′ I 和 I' I和I′ 分别表示目标图像和参考图像。 我们使用 SURF [1] 来检测和匹配特征,并使用 LSD [26] 来检测线条。 然后,我们可以根据相应区域内的一系列 CN 值计算候选子区域之间的相似度 [10]。 对于相似度最高的匹配子区域 R e g ∈ I 和 R e g ′ ∈ I ′ Reg ∈ I 和 Reg' ∈ I' Reg∈I和Reg′∈I′,使用匹配区域内现有的匹配点对构建 CN,如图 2 左图所示。 △ K l 1 U 1 K l 2 \triangle K^1_l U_1 K^2_l △Kl1U1Kl2 上的 U 1 , U 2 、 U 3 , U 4 , U 5 , U 6 U_1, U_2、U_3,U_4,U_5,U_6 U1,U2、U3,U4,U5,U6,以及 △ K l 1 ′ U 1 ′ K l 2 ′ \triangle K^{1′}_l U^′_1K_l^{2'} △Kl1′U1′Kl2′上的对应点KaTeX parse error: Double superscript at position 36: …′_4、U^′_5、U^′_6'̲ 被添加到匹配点集中以增加用于翘曲的锚点。 最后,我们使用 RANSAC [7] 来细化匹配点并估计其局部单应性 H,用于在子区域 [10] 中获得更多匹配的线。
3.3 基于双特征的预对齐
设 $p_i = (x_i, y_i, 1) 和 p^\prime_i = (x^\prime_i, y^\prime_i , 1) $为匹配点对 { ( p i , p i ′ ) } i = 1 , 2 , . . . , N \{(p_i, p^\prime_i)\}_{i=1,2,...,N} {(pi,pi′)}i=1,2,...,N在齐次坐标中,其中 N 是匹配点对的数量,对于匹配线对集合 { ( l j , l j ′ ) } j = 1 , 2 , . . . , L , l j ∈ I 和 l j ′ ∈ I ′ \{(l_j , l^\prime_j )\}_{j=1,2,...,L}, l_j ∈ I 和 l^\prime_ j ∈ I^\prime {(lj,lj′)}j=1,2,...,L,lj∈I和lj′∈I′,其中 L 是匹配线对的数量。 线 l j l_j lj 表示为$ (l^s_j, l^e_j)$,其中 l j s 和 l j e l^s_j 和 l^e_j ljs和lje 是两个端点。 为了获得更好的配准,应该最小化扭曲后匹配点和线之间的欧几里得距离。 我们将 H 表示为初始单应性, H ∗ H_∗ H∗ 是 H 的向量表达式, H ^ ∗ \hat H_* H^∗ 是期望的单应性。 因此,基于对偶特征的全局单应性可以表示为

其中 d i s ( l j ′ , H L j s , e ) dis(l^\prime_j,HL_j^{s,e}) dis(lj′,HLjs,e) 表示终点 H L j s , e HL_j^{s,e} HLjs,e 和线 l j ′ , H ∗ ∈ R 9 l^\prime_j, H_* \in R^9 lj′,H∗∈R9。 U i ∈ R 2 × 9 , V j ∈ r 2 × 9 U_i \in R^{2\times 9}, V_j\in r^{2\times 9} Ui∈R2×9,Vj∈r2×9 。通过 SVD 可以很容易最小化函数 [ U i , V j ] T H ∗ = 0 [U_i, V_j]^T H_*=0 [Ui,Vj]TH∗=0。此外,我们使用归一化和坐标轴旋转来提高模型 [4] 和 [17] 的稳定性和准确性。
4. 全局线指导的网格变形
预对齐估计的全局单应性只提供了一个近似的变换,但仍然存在失真和弯线。 凸线越长,直线弯曲越大。 为了解决这个问题,我们探索了线保持约束的全局共线结构,并将其与点线对齐和能量函数中的失真项结合起来。
4.1 能量函数定义
首先,我们为每个图像对构建矩形网格。 令 I 和 I ’ 分别表示目标和参考图像。 假设网格网格顶点的索引是从 1 到 n。 向量 $V = [x_1 y_1 x_2 y_2 ···x_n y_n]^T (V ∈ R^{2n}) $ 用于描述原始顶点的坐标,向量 $\hat V = [\hat x_1 \hat y_1 \hat x_2 \hat y_2··· \hat x_n \hat y_n]^T (\hat V ∈ R^{2n} ) $表示扭曲顶点的坐标。 对于任何样本点 p ∈ I,我们通过其四个封闭网格顶点的双线性插值将其表示为 τ §。 然后,对应的翘曲点pb表示为 τ ( p ^ ) τ(\hat p) τ(p^)。 总能量函数 E ( V ^ ) E(\hat V) E(V^) 为

其中 E l p ( V ^ ) E_{lp}(\hat V) Elp(V^) 是通过保持局部和全局的线的线保留项, E a ( V ^ ) E_a(\hat V) Ea(V^) 是通过改进匹配点线的对应关系的点线对齐项,而 E d V ^ E_d{\hat V} EdV^ 是通过保留网格线的斜率和均匀 warp 相邻网格的失真控制项。
4.2 线保留项
局部单个显着线和全局共线线段对于扭曲都是至关重要的。 因此,行保留项定义为:

如图 4 所示,局部红线 l 1 , . . , l 5 l_1, . . , l_5 l1,..,l5 在空间上是分开的,但它们是共线的,如全局蓝线 l 6 l_6 l6 所示。如图 4 中的第二幅图像所示,可以保留局部线结构,但它们的共线性在翘曲过程中很容易被破坏。由于这种失真对人类对图像质量的感知非常令人不安,我们设计了一种局部扭曲的合并策略,通过评估线段的共线性来保持全局线性结构,这是我们的主要贡献之一。合并过程在算法 1 中有详细说明。我们每次都评估成对的线,合并的线应该满足三个约束:
-
首先,两条线 s l o p e ( l i ) slope(l_i) slope(li)和 s l o p e ( l j ) slope(l_j) slope(lj) 的斜率应该接近。
-
其次,从端点到另一条线的距离,即 d i s ( l j , p l i e ) 和 d i s ( l j , p l i s ) dis(l_j , p^e_{l_i} ) 和 dis(l_j , p^s_{l_i}) dis(lj,plie)和dis(lj,plis) 应该很小。
-
第三,两条线的相邻端点 d i s ( p l i e , p l j s ) dis(p^e_{l_i}, p^s_{l_j}) dis(plie,pljs) 的距离应该很小,如图 4 所示。
注意我们引入了 flag 以避免合并线的无限循环,最初设置为 0 和合并后设置为1。虽然局部线最有可能通过原始线拟合获得,但全局线通常来自合并过程。值得注意的是,每条线的长度 len (l) 用于通过阈值 µ 对局部和全局线段进行分类。

这里我们从全局线集合 S g l S_{gl} Sgl 中的直线 { l g } g = 1 , 2 , . . . , Q \{l_g\}_{g=1,2,...,Q} {lg}g=1,2,...,Q 作为一个例子,其中 Q 表示线的数量。每条线都是均匀采样了 M g M_g Mg 个点 { p k g } k = 1 , 2 , . . . , M g g = 1 , 2 , . . . , Q \{p_k^g\}_{k=1,2,...,M_g}^{g=1,2,...,Q} {pkg}k=1,2,...,Mgg=1,2,...,Q,则:
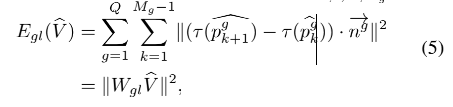
其中 n → g \overrightarrow n^g ng 表示 l g l_g lg 的归一化向量, W g l ∈ R ( ∑ g = 1 Q ( M g − 1 ) ) × 2 n W_{gl} \in R^{(\sum_{g=1}^Q(M_g-1))\times 2n} Wgl∈R(∑g=1Q(Mg−1))×2n 。我们采用相同的方法来构建对局部线段的约束项。

4.3 点线对齐和失真控制
点-线对齐项是基于一个直观的约束来定义的,即匹配的点和线对在扭曲后应该相互重合,定义为
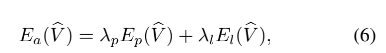
E p ( V ^ ) 和 E l ( V ^ ) E_p(\hat V) 和 E_l(\hat V) Ep(V^)和El(V^) 分别是点和线的对齐项。
为了控制目标图像I的畸变,构造了一系列水平和垂直线,称为交叉线。 这些构造的线被认为是图像 I 的固有线性结构,如图 5 中的红线所示。线的斜率和它们交叉点之间的空间用于控制失真。 失真项由全局项 Edg 和非重叠项 Edn 定义

由于所有约束项都是二次的,因此可以通过稀疏线性求解器对其进行重新公式化和最小化。 更多细节可以在[17]中找到。 翘曲结果与 SPW [17] 进行比较,后者也具有线约束。 两种方法对于原始目标图像 I 具有相同数量的均匀间隔交叉线。 翘曲结果如图 5 所示,我们的方法表现出密集的交叉线和从重叠区域到非重叠区域的适度过渡,表现出对失真的良好控制,而 SPW [17] 的结果中出现了明显的失真,如图放大的矩形。

5. 共线性的定量评价
为了量化线性结构的拼接性能,我们设计了一种新的评估方法,该方法考虑了三个方面:
- 点的共线性
- 匹配线的距离
- 匹配线方向的差异。
我们在 l j l_j lj 线上统一采样 P s P_s Ps 个点 { p k j } k = 1 , 2 , . . . , P s \{p^j_k\}_{k=1,2,...,P_s} {pkj}k=1,2,...,Ps,在图 6 中用红色标记。图 6 左下图展示了拟合线 $l^π_j = π({\hat d^j_k}_{k=1,2,…,P_s} ) $通过最小二乘法得到扭曲点 { d ^ k j } k = 1 , 2 , . . . , P s \{\hat d^j_k\}_{k=1,2,...,P_s} {d^kj}k=1,2,...,Ps。 对于 L 条线的误差项 E e r r E_{err} Eerr 定义为:
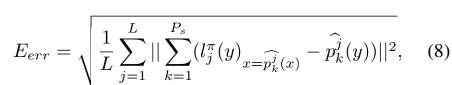
其中 p ^ k j ( y ) \hat p^j_k(y) p^kj(y) 表示 p ^ k j \hat p_k^j p^kj 的 y 坐标,而 l j π ( y ) x = p ^ k j ( x ) l_j^\pi(y)_{x=\hat p^j_k(x)} ljπ(y)x=p^kj(x) 表示和 p ^ k j \hat p_k^j p^kj拥有相同 x 坐标的 l j π l_j^\pi ljπ 的 y 坐标。
正如图 6 右上图所示,距离项 E d i s E_{dis} Edis 表示两个匹配的终点和匹配线段的距离,定义如下:

其中 p ^ 1 j , p ^ P s j \hat p_1^j,\hat p_{P_s}^j p^1j,p^Psj 表示 l ^ j \hat l_j l^j 的两个终点。

方向项 E d i r E_{dir} Edir 估计扭曲线和匹配线之间的方向差异。我们分别用 l ^ j → , l j ′ → \overrightarrow{\hat l_j}, \overrightarrow{l_j^\prime} l^j,lj′ 表示线 l ^ j , l j ′ \hat l_j, l_j^\prime l^j,lj′ 的方向向量。具有较小 x 坐标的端点用作每个向量的起点。 如图 6 右下图所示,两条线的叉积 l j ′ → × l j → = l e n ( l j ′ ) × l e n ( l ^ j ) × s i n ( θ ) \overrightarrow{l_j^\prime}\times \overrightarrow{l_j }=len(l_j^\prime)\times len(\hat l_j)\times sin(\theta) lj′×lj=len(lj′)×len(l^j)×sin(θ) 可以反映两个向量的方向差异,也取 $len(l_j^\prime)和 len(\hat l_j ) $两行的长度,因此,对于所有直线的 E d i r E_{dir} Edir 表示为:
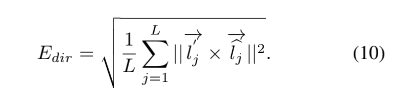
6. 实验
我们通过消融研究证明了所提出方法的有效性,并在 15 个测试图像对上与最新技术进行了定量和定性比较,这些图像对涵盖了不同类型的数据集,涉及相机运动、场景和视场 . 输入图像对的大小调整为 1000 × 800 像素,每个网格的大小为 40 × 40。这使我们能够保持所有参数不变。 划分局部和全局线段的阈值 µ 设置为网格对角线长度的三倍。 在能量函数中, λ l o 和 λ g l λ_{lo} 和 λ_{gl} λlo和λgl 设置为 50 和 100 以保持线, λ p 和 λ l λ_p 和 λ_l λp和λl 设置为 1 和 5 用于点线对齐, λ d g 和 λ d n λ_{dg} 和 λ_{dn} λdg和λdn 设置为 50 和 100 以最小化失真。
6.1 消融实验
一致的线和点约束可以提供准确的对齐并抑制伪影。我们用单独的点和线匹配策略[17]代替我们的联合匹配策略,其他部分保持不变。示例结果如图 8 所示。共有三个拼接实例,放大的重叠区域显示在每个结果的右侧。正如我们所看到的,我们的关节点和线匹配在图 8(b)中产生了清晰的拼接结果,而在图 8(a)中存在明显的伪影。

线性结构保持可以保持局部和全局线性结构并抑制失真,如图9所示。在图9(a)中,局部形状得到了很好的保留,但线条在没有线性约束的情况下弯曲。当我们粗略地使用 LSD 检测到的线时,建筑物和地面上的短线要好得多,但仍然不够直。特别是,自行车在图 9(b)中有严重的变形。相比之下,局部和全局线性约束在我们的方法中得到了很好的平衡,如图 9© 所示。

6.2 对比 state-of-the-arts
进行了几个实验以将拼接结果与现有方法进行比较,包括 SVA [21]、CPW [22]、APAP [30]、ELA [14]、SPHP [4]、GSP [5] 和 SPW [17] .定量和定性结果来自他们的论文或发布的代码。
我们对点和线都采用定量评价。点的对齐精度由一组匹配点上的均方根误差 (RMSE) [30] 来衡量。表 1 描述了第一列中命名的 7 个图像对的 RMSE 值。我们的方法在所有 7 对上产生了最低的错误。我们的平均误差为 1.7014,比 SPW 低 31%。此外,我们的误差方差为 0.05,比 SPW 的值 0.75 低 93%。

此外,我们使用我们在第五节中提出的三个措施来评估线性结构。 在图 7 中,我们将我们的方法与 SPW [17] 进行比较,后者具有局部但没有全局线约束。如图 7 所示,x 坐标表示图像对的名称,垂直坐标表示误差。我们的方法在共线性和角度差方面优于 SPW,如图 7(a) 和图 7© 所示。在图 7(b) 中,我们的误差方差为 0.0855,比 SPW 的 0.6630 小 87.11%,表明所有对的发散误差都较小。在图像对“学校”和“建筑”上,SPW 发生了严重变化,我们的错误大约是我们的两倍。
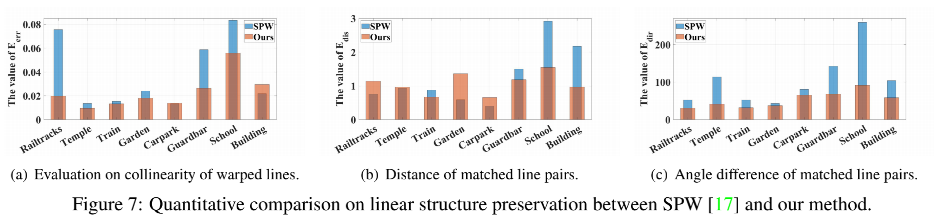
图 10 展示了全面的视觉比较。我们的方法在保留线性结构和产生清晰且无伪影的重叠区域方面优于所有其他方法。 前四行的线性结构都表现出严重的弯曲,用红色标记。 在放大的矩形中显示的现有方法的结果中出现了明显的伪影,例如花朵、桌子和遮阳伞。

7.结论
我们提出了一种基于线引导变形和线点约束的结构保持图像拼接方法。 我们将输入图像划分为子区域,并通过线点不变量进行匹配。 局部匹配为预对齐提供准确的线和点对,在重叠区域没有显示模糊或伪影。 我们提出了一种线引导扭曲来保留局部和全局结构,同时消除非重叠区域的失真。 此外,我们为线性结构设计了一种新的定量评估方法,这与人类的感知一致,因为人类视觉对线性结构的扭曲非常敏感。 实验结果表明,所提出的方法在具有挑战性的测试图像上准确地对齐重叠区域和非重叠区域,并且与现有技术相比产生了明显更好的性能。
这篇关于【论文笔记】Leveraging Line-point Consistence to Preserve Structures for Wide Parallax Image Stitching的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







