Python实现非调库的决策树算法

一、决策树的算法原理

决策树的英文名叫“Decision Tree”，它的用途通俗来讲就是用一个树状图对某一对象的多个属性逐条分析，最后得出这个对象应该属于哪一个类别。它是一种分类的方法。
下面我们用一个老生常谈的西瓜案例来讲解其原理。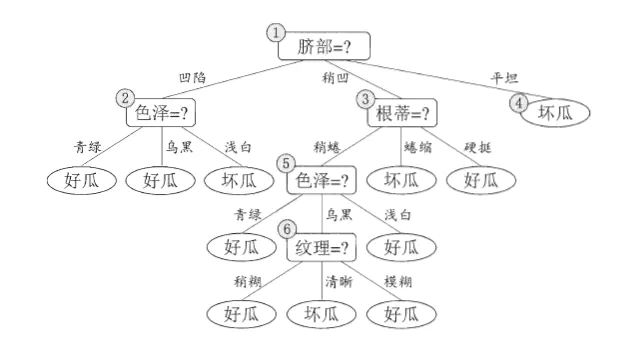
如图是一个标准的决策树。对于这个西瓜的集合，我们有脐部、色泽、根蒂、纹理这四种属性可以用于构建决策树，而好瓜和坏瓜则是分类的结果。
这样，当我们拿到一个西瓜对象，我们先看它的脐部属性：若为平坦，则判断为坏瓜；若为凹陷，再进一步看色泽：色泽青绿与乌黑是好瓜，色泽浅白是坏瓜。以此类推，对任一个西瓜对象我们都能经过若干步的判断来得知是好瓜还是坏瓜。
当然，决策树并不能保证得出一定正确的分类结果，但我们的决策树应该保证尽量高的准确度。

决策树的构建

那么，应该如何保证我们的决策树有最高的准确度呢？
我们知道，待分类的对象有多个属性（脐部、色泽、根蒂、纹理），那么为什么在这些属性中要先进行脐部的判断，而不是纹理或色泽呢？
如果我们希望分类结果尽可能的好，那么就应该在划分时让各个分区尽可能的“纯”。我们需要一种分裂规则，它可以得出哪个属性最适合作为分裂属性用于本层级的决策树构建。我们采纳这种规则，得知在第一次划分时脐部是最合适的分裂属性，所以我们选择了它而不是别的。在决策树构建这一方面有多种规则，而本文使用的是ID3算法。

ID3算法

我们要引入如下概念：

1. 信息熵
   其计算公式如下：
   $$Info(D)=-\sum _{i=0}^m{p}_{i}lo{g}_2(p_i)\text{\hspace{1em}(1)}$$
   乍一看很复杂，但其实很简单，我们用一个例子来解释它。
   首先，D是西瓜的一个集合。
   在集合D内有5个对象，其结果有好瓜、坏瓜两类，结果的类别数就是m。
   各类中各有2、3个对象，那么它们各自的占比2/5、3/5就是各个p。
   则$Info(D)=-\frac{2}{5}lo{g}_2(\frac{2}{5})-\frac{3}{5}lo{g}_2(\frac{3}{5})$
2. 信息增益
   同样对于这个D，我们选择了某一个属性A进行分类，那么有
   $$Inf{o}_A(D)=\sum _{j=1}^v\frac{|D_j|}{|D|}\times Info(D_j)\text{\hspace{1em}(2)}$$
   继续使用1.中的例子。假如A是属性色泽，坏瓜类中有2个乌黑，1个浅白，好瓜类中有1个乌黑，1个浅白，则$Inf{o}_A(D)=\frac{3}{5}\times (-\frac{2}{3}lo{g}_2\frac{2}{3}-\frac{1}{3}lo{g}_2\frac{1}{3})+\frac{2}{5}\times (-\frac{1}{2}lo{g}_2\frac{1}{2}-\frac{1}{2}lo{g}_2\frac{1}{2})$
   由此，信息增益
   $$Gain(A)=Info(D)-Inf{o}_A(D)\text{\hspace{1em}(3)}$$
   它定义为原来的信息需求（基于结果类划分）和新的信息需求（基于属性A划分）之间的差。
3. 基尼系数（补充）
   它用于衡量某个集合的不纯度，主要在CART算法中应用，定义为
   $$Gini(D)=1-\sum _{i=1}^m{p}_i^2$$
   继续沿用上面的例子，有$Gini(D)=1-(\frac{2}{5}{)}^2-(\frac{3}{5}{)}^2$

在决策树的构建中，我们在每一次层次都选择具有最高信息增益的属性作为分裂属性。之后再在分裂属性划分出的子集中继续选择新的分裂属性，如此循环下去，最终得到想要的决策树。

终止条件

任何一个算法的步骤都不能是无限的，决策树也同理。一般来说，有如下几个条件可用于参考以终止分裂：

1. 节点数
   当节点的数据量小于一个指定的数量时，不继续分裂。两个原因：一是数据量较少时，再做分裂容易强化噪声数据的作用；二是降低树生长的复杂性。提前结束分裂一定程度上有利于降低过拟合的影响。
2. 分类结果纯度
   在数据量很大时，在某次分类得到的结果中，如果某一类已经占绝大多数，可以认为已经达到了停止分裂的条件。可以用基尼系数进行判别，也可以自行选用其他方法。
3. 树的深度
   树的深度即叶节点与根节点的最长距离。当深度达到设定的阈值便可以停止分裂。

属性值连续的情况

我们在上面讨论的情况都是基于各属性不连续的条件下得出的结果。所谓不连续即属性的划分是标称型的，如纹理的稍糊、清晰、模糊。
但有时候，我们要处理一些连续的属性，如高度，年龄等，这时候就需要改变处理。将连续的各值按升序排列，取每两个值的中间值作为可能的分裂点，依次计算其信息增益，从中选出分裂点。在每一个新划分出的子集中，都要重新计算分裂点。

二、代码实现

本文选用的是鸢尾花数据集，详细数据集可以在UCI数据库中找到，网上也有众多资源，也可以用后文提供的网盘资源。
在数据处理上，选择了Pandas的DataFrame，它可以方便地直接在相应的行或列中按条件筛选出所需数值并统计。
源数据资源
网盘链接：https://pan.baidu.com/s/1UKcJnUGLCdWp5KtJIbZHBw
提取码：wyxz

具体过程

首先，我们读入数据，并人为划分出训练集与测试集。

import pandas as pd#pandas库用于处理读取的数据
import numpy as np
import randomcsvFile = pd.read_csv('iris.csv')
dataset = csvFile.values.tolist()#读入.csv文件后，其数字是用str的形式存储的，用.values方法转为用float的形式存储#用随机的方法选出测试集，原集合删去测试集的数据作为训练集使用
test = []
n_test = int(0.2*len(dataset))
for i in range(n_test):k = random.randint(0,len(dataset)-1)test.append(dataset[k])del dataset[k]

预设一些会用到的变量。

n = len(dataset)
feature = ['萼长','萼宽','瓣长','瓣宽','花类']
feature_num = len(feature) - 1
df = pd.DataFrame(dataset, columns = feature)#重新转为dataframe形式
iris = ['Iris-setosa','Iris-versicolor','Iris-virginica']

下一步即是进行决策树的构建。division函数将返回当前子集的最佳分裂点以及这一划分的$Inf{o}_A(D)$。
在构建决策树时，每一步都需要进行信息增益的计算，而其中计算信息熵的时候会有$lo{g}_{2}0$的存在，这在函数中是不允许的，所以我们还需要自定义一个log2函数。

def log2(x):   return 0 if x==0 else np.log2(x)def entropy_calc(df):    entropy = 0for e in iris:perc = df.loc[df['花类']==e]['花类'].count()/nentropy -= perc*log2(perc)return entropy    def division(df, i):n = len(df)arr = np.unique(df[feature[i]].tolist())#unique可以将列表元素去重并排好序，arr用于存储某属性下的各个值min_exp = float('inf')split = 0for k in range(len(arr)-1):cur_split = (arr[k]+arr[k+1])/2        num_low = df.loc[df[feature[i]]<=cur_split][feature[i]].count()num_high = n - num_lowperc1, perc2 = 0, 0info1, info2 = 0, 0for e in iris:perc1 = float(df.loc[(df['花类']==e)&(df[feature[i]]<=cur_split), ['花类']].count())/num_low           info1 -= perc1*log2(perc1)perc2 = float(df.loc[(df['花类']==e)&(df[feature[i]]>cur_split), ['花类']].count())/num_highinfo2 -= perc2*log2(perc2)info_a = num_low/n*info1 + (1-num_low/n)*info2if info_a <= min_exp:min_exp = info_asplit = cur_splitreturn split, min_exp

之后需要设定判断是否终止分裂的judge函数。

def judge(df):n = len(df)perc_list = []#计算是否有某个类别在当前子集占绝大多数。如果是，则直接返回其名称。for e in iris:perc = df.loc[df['花类']==e]['花类'].count()/nif perc>0.9:return eperc_list.append(perc)#若当前子集数目过少，则直接返回占比最大的鸢尾花的类别    if n<=5:return iris[perc_list.index(max(perc_list))]#若前两条都不满足，则表明可以继续进行分裂return 'null'

最后，用递归的方式编写主体运行函数。

def program(df, tree):   flag = judge(df)if flag=='null':point, info_a, gain = [], [], []#此三者用于存储分类中产生的分裂点、Info_A、信息增益info = entropy_calc(df)for i in range(feature_num):       answer = division(df,i)point.append(answer[0])info_a.append(answer[1])gain.append(info - info_a[i])best_feature = gain.index(max(gain)) #df_l与df_r用于存储按分裂点分出的子集     df_l = df.loc[df[feature[best_feature]]<=point[best_feature]]df_r = df.loc[df[feature[best_feature]]>point[best_feature]]tree.extend([feature[best_feature],point[best_feature],[],[]])program(df_l,tree[2])program(df_r,tree[3])  #若已判定为可以停止分裂，则tree直接append得到的分类结果   else:tree.append(flag)tree = []#用列表形式存放最终的决策树
program(df,tree)
print(tree)

最终生成的决策树形式如下：

['瓣长', 2.45, ['Iris-setosa'], ['瓣宽', 1.65, ['Iris-versicolor'], ['Iris-virginica']]]

列表内的每一层的[0]为选择的分裂属性，[1]为分裂点。[3]、[4]分别为属性的值小于、大于分裂点所进入的分支。

此后，还可以进一步利用此前分出的测试集计算所生成决策树的准确度。check函数用于将测试集数据套入决策树与结果比较。

hit = 0
def check(tree, flower):global hit#走入决策树的叶节点后，判断是否符合if len(tree)==1:if tree[0] == flower[4]:hit += 1return#根据决策树提供的属性进行数据对比决定进入左侧或右侧的分支if flower[feature.index(tree[0])]<tree[1]:check(tree[2], flower)else:check(tree[3], flower)for flower in test:check(tree, flower)print(hit/n_test)

完整代码

import pandas as pd#pandas库用于处理读取的数据
import numpy as np
import randomcsvFile = pd.read_csv('iris.csv')
dataset = csvFile.values.tolist()#读入.csv文件后，其数字是用str的形式存储的，用.values方法转为用float的形式存储#用随机的方法选出测试集，原集合删去测试集的数据作为训练集使用
test = []
n_test = int(0.2*len(dataset))
for i in range(n_test):k = random.randint(0,len(dataset)-1)test.append(dataset[k])del dataset[k]n = len(dataset)
feature = ['萼长','萼宽','瓣长','瓣宽','花类']
feature_num = len(feature) - 1
df = pd.DataFrame(dataset, columns = feature)#重新转为dataframe形式
iris = ['Iris-setosa','Iris-versicolor','Iris-virginica']def log2(x):   return 0 if x==0 else np.log2(x)def entropy_calc(df):    entropy = 0for e in iris:perc = df.loc[df['花类']==e]['花类'].count()/nentropy -= perc*log2(perc)return entropy    def division(df, i):n = len(df)arr = np.unique(df[feature[i]].tolist())#unique可以将列表元素去重并排好序，arr用于存储某属性下的各个值min_exp = float('inf')split = 0for k in range(len(arr)-1):cur_split = (arr[k]+arr[k+1])/2        num_low = df.loc[df[feature[i]]<=cur_split][feature[i]].count()num_high = n - num_lowperc1, perc2 = 0, 0info1, info2 = 0, 0for e in iris:perc1 = float(df.loc[(df['花类']==e)&(df[feature[i]]<=cur_split), ['花类']].count())/num_low           info1 -= perc1*log2(perc1)perc2 = float(df.loc[(df['花类']==e)&(df[feature[i]]>cur_split), ['花类']].count())/num_highinfo2 -= perc2*log2(perc2)info_a = num_low/n*info1 + (1-num_low/n)*info2if info_a <= min_exp:min_exp = info_asplit = cur_splitreturn split, min_expdef judge(df):n = len(df)perc_list = []#计算是否有某个类别在当前子集占绝大多数。如果是，则直接返回其名称。for e in iris:perc = df.loc[df['花类']==e]['花类'].count()/nif perc>0.9:return eperc_list.append(perc)#若当前子集数目过少，则直接返回占比最大的鸢尾花的类别    if n<=5:return iris[perc_list.index(max(perc_list))]#若前两条都不满足，则表明可以继续进行分裂return 'null'def program(df, tree):   flag = judge(df)if flag=='null':point, info_a, gain = [], [], []#此三者用于存储分类中产生的分裂点、Info_A、信息增益info = entropy_calc(df)for i in range(feature_num):       answer = division(df,i)point.append(answer[0])info_a.append(answer[1])gain.append(info - info_a[i])best_feature = gain.index(max(gain)) #df_l与df_r用于存储按分裂点分出的子集     df_l = df.loc[df[feature[best_feature]]<=point[best_feature]]df_r = df.loc[df[feature[best_feature]]>point[best_feature]]tree.extend([feature[best_feature],point[best_feature],[],[]])program(df_l,tree[2])program(df_r,tree[3])  #若已判定为可以停止分裂，则tree直接append得到的分类结果   else:tree.append(flag)tree = []#用列表形式存放最终的决策树
program(df,tree)
print(tree)hit = 0
def check(tree, flower):global hit#走入决策树的叶节点后，判断是否符合if len(tree)==1:if tree[0] == flower[4]:hit += 1return#根据决策树提供的属性进行数据对比决定进入左侧或右侧的分支if flower[feature.index(tree[0])]<tree[1]:check(tree[2], flower)else:check(tree[3], flower)for flower in test:check(tree, flower)print(hit/n_test)