【数据结构】线性表（六）堆栈：顺序栈及其基本操作（初始化、判空、判满、入栈、出栈、存取栈顶元素、清空栈）

2023-10-20 13:52
文章标签 元素 数据结构 基本操作 初始化 顺序 线性表 判空 存取 清空 堆栈 出栈 判满 入栈 栈顶

本文主要是介绍【数据结构】线性表（六）堆栈：顺序栈及其基本操作（初始化、判空、判满、入栈、出栈、存取栈顶元素、清空栈），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

文章目录

  • 一、堆栈
    • 1. 定义
    • 2. 基本操作
  • 二、顺序栈
    • 0. 顺序表
    • 1. 头文件和常量
    • 2. 栈结构体
    • 3. 栈的初始化
    • 4. 判断栈是否为空
    • 5. 判断栈是否已满
    • 6. 入栈
    • 7. 出栈
    • 8. 查看栈顶元素
    • 9. 清空栈
    • 10. 主函数
    • 11. 代码整合

  堆栈Stack 和 队列Queue是两种非常重要的数据结构，两者都是特殊的线性表：

  • 对于堆栈，所有的插入和删除（以至几乎所有的存取）都是在表的同一端进行
  • 对于队列，所有的插入都是在表的一端进行，所有的删除（以至几乎所有的存取）都是在表的另一端进行。

一、堆栈

1. 定义

  堆栈（简称栈）是一种操作受限的线性表，只允许在表的同一端进行插入和删除操作，且这些操作是按后进先出的原则进行的。进行插入和删除的一端被称为栈顶，另一端被称为栈底。当栈中无元素时称其为空栈。根据上述定义，每次删除（退栈）的总是最后插入（进栈）的元素。

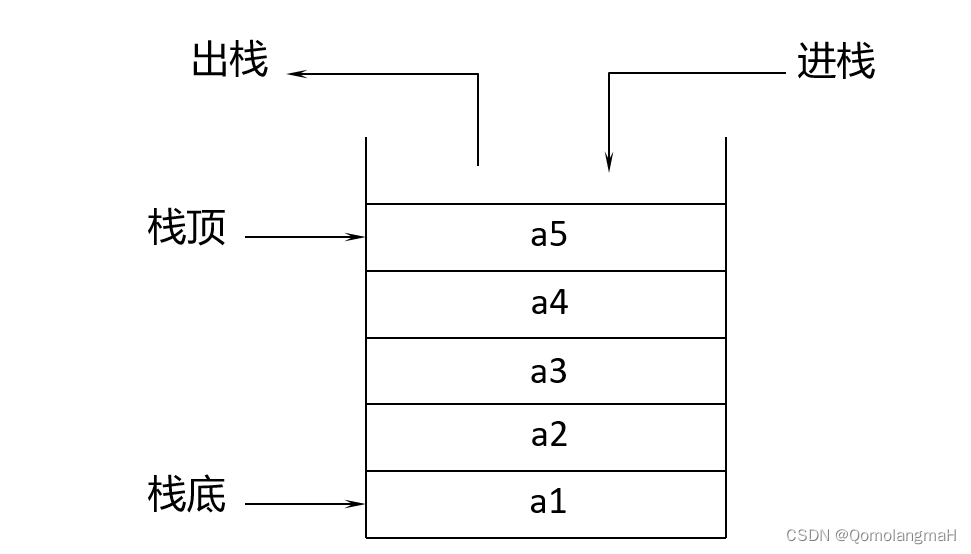
堆栈示意图
  如图所示的堆栈中，诸元素以a1，a2，a3，a4，a5的顺序进栈，而退栈的次序则是a5，a4，a3，a2，a1。 也就是说，从栈中取走元素是按后进先出的原则进行的，因此栈又被称作后进先出（Last in First Out）的线性表，简称为LIFO表。

2. 基本操作

  • 堆栈是受限的线性表，其基本操作包括
    • push ( ) : 压入一个元素（插入）；
    • pop ( ) : 弹出一个元素（删除）；
    • peek ( ) : 存取栈顶元素值；
    • clear ( ) : 清空栈；
    • IsEmpty ( ) : 判断栈是否为空；
  • 同普通线性表一样，堆栈也可以用顺序存储和链接存储两种方式来实现：

二、顺序栈

  用顺序存储方式实现的堆栈称为顺序栈。

  • 顺序栈用数组存放栈元素，可方便地进行各种栈操作；
  • 某一堆栈的规模指该堆栈最多能容纳的元素个数；
  • 存放堆栈的数组规模（或大小）应按堆栈的规模来确定：
    • 当堆栈中元素的个数达到堆栈规模（简称为栈满）时，则无法再向堆栈插入元素，换言之此时的插入操作将产生上溢出。
  • 如何确保既不上溢也不下溢？
    • 需要一个整型变量size来存放数组规模，以及一个整型变量top来存放栈顶元素在数组中的位置（下标）
      • 当栈为空时，top值为0
      • 每入栈（或出栈）一个元素，top值加1（或减1）
      • 当top等于size时，说明栈满

0. 顺序表

参考前文：顺序表及其基本操作

1. 头文件和常量

   #include <stdio.h>#include <stdlib.h>#define MAX_SIZE 100
  • 两个头文件
    • stdio.h用于输入输出操作
    • stdlib.h用于内存分配和释放
  • 通过#define指令定义了一个常量MAX_SIZE，它表示栈的最大容量为100。

2. 栈结构体

   typedef struct {int data[MAX_SIZE];int top;} Stack;

  使用结构体定义了一个栈的数据结构，data是一个整型数组，用于存储栈中的元素，top表示栈顶的索引。

3. 栈的初始化

   void init(Stack* stack) {stack->top = -1;}

  初始化栈，将栈顶索引top置为-1，表示栈为空。

4. 判断栈是否为空

   int isEmpty(Stack* stack) {return stack->top == -1;}

  判断栈是否为空，如果栈顶索引top等于-1，表示栈为空，函数返回1；否则，返回0。

5. 判断栈是否已满

   int isFull(Stack* stack) {return stack->top == MAX_SIZE - 1;}

  isFull函数用于判断栈是否已满，如果栈顶索引top等于MAX_SIZE - 1，表示栈已满，函数返回1；否则，返回0。

6. 入栈

   void push(Stack* stack, int value) {if (isFull(stack)) {printf("Stack is full. Cannot push element.\n");return;}stack->data[++stack->top] = value;}

  push函数用于将元素入栈，首先判断栈是否已满，如果已满，则打印错误信息并返回；否则，将元素存储在栈顶索引top的位置，并将栈顶索引加1。

7. 出栈

   int pop(Stack* stack) {if (isEmpty(stack)) {printf("Stack is empty. Cannot pop element.\n");return -1;}return stack->data[stack->top--];}

  pop函数用于将栈顶元素出栈，首先判断栈是否为空，如果为空，则打印错误信息并返回-1；否则，返回栈顶元素的值，并将栈顶索引减1。

8. 查看栈顶元素

   int peek(Stack* stack) {if (isEmpty(stack)) {printf("Stack is empty. Cannot peek element.\n");return -1;}return stack->data[stack->top];}

  peek函数用于查看栈顶元素的值，首先判断栈是否为空，如果为空，则打印错误信息并返回-1；否则，返回栈顶元素的值。

9. 清空栈

   void clear(Stack* stack) {stack->top = -1;}

  clear函数用于清空栈，将栈顶索引top置为-1，表示栈为空。

10. 主函数

int main() {Stack stack;init(&stack);push(&stack, 10);push(&stack, 20);push(&stack, 30);printf("Top element: %d\n", peek(&stack));printf("Popped element: %d\n", pop(&stack));printf("Popped element: %d\n", pop(&stack));printf("Is stack empty? %s\n", isEmpty(&stack) ? "Yes" : "No");clear(&stack);printf("Is stack empty? %s\n", isEmpty(&stack) ? "Yes" : "No");return 0;
}

  • 声明一个Stack类型的变量stack，然后调用init函数对栈进行初始化。

  • 使用push函数将元素10、20和30依次入栈。

  • 使用peek函数查看栈顶元素的值。

  • 使用pop函数将栈顶的两个元素出栈。

  • 使用isEmpty函数判断栈是否为空。

  • 调用clear函数清空栈。

  • 再次使用isEmpty函数判断栈是否为空。

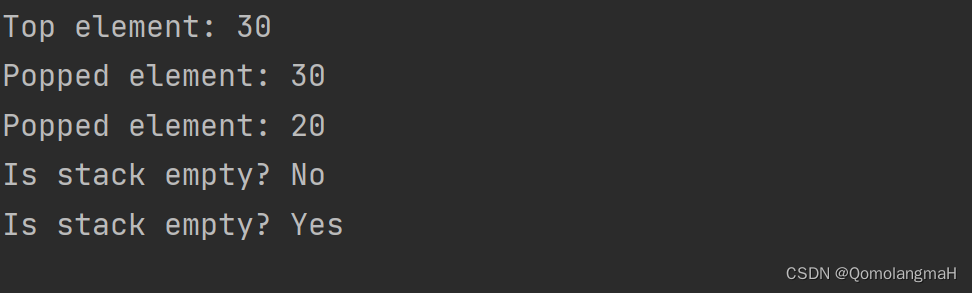
在这里插入图片描述

11. 代码整合

#include <stdio.h>
#include <stdlib.h>#define MAX_SIZE 100typedef struct {int data[MAX_SIZE];int top;
} Stack;void init(Stack* stack) {stack->top = -1;
}int isEmpty(Stack* stack) {return stack->top == -1;
}int isFull(Stack* stack) {return stack->top == MAX_SIZE - 1;
}void push(Stack* stack, int value) {if (isFull(stack)) {printf("Stack is full. Cannot push element.\n");return;}stack->data[++stack->top] = value;
}int pop(Stack* stack) {if (isEmpty(stack)) {printf("Stack is empty. Cannot pop element.\n");return -1;}return stack->data[stack->top--];
}int peek(Stack* stack) {if (isEmpty(stack)) {printf("Stack is empty. Cannot peek element.\n");return -1;}return stack->data[stack->top];
}void clear(Stack* stack) {stack->top = -1;
}int main() {Stack stack;init(&stack);push(&stack, 10);push(&stack, 20);push(&stack, 30);printf("Top element: %d\n", peek(&stack));printf("Popped element: %d\n", pop(&stack));printf("Popped element: %d\n", pop(&stack));printf("Is stack empty? %s\n", isEmpty(&stack) ? "Yes" : "No");clear(&stack);printf("Is stack empty? %s\n", isEmpty(&stack) ? "Yes" : "No");return 0;
}

这篇关于【数据结构】线性表（六）堆栈：顺序栈及其基本操作（初始化、判空、判满、入栈、出栈、存取栈顶元素、清空栈）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/247553。

相关文章

JVM 的类初始化机制

JVM 的类初始化机制

前言 当你在 Java 程序中new对象时，有没有考虑过 JVM 是如何把静态的字节码（byte code）转化为运行时对象的呢，这个问题看似简单，但清楚的同学相信也不会太多，这篇文章首先介绍 JVM 类初始化的机制，然后给出几个易出错的实例来分析，帮助大家更好理解这个知识点。 JVM 将字节码转化为运行时对象分为三个阶段，分别是：loading 、Linking、initialization
阅读更多...
【数据结构】——原来排序算法搞懂这些就行，轻松拿捏

【数据结构】——原来排序算法搞懂这些就行，轻松拿捏

前言：快速排序的实现最重要的是找基准值，下面让我们来了解如何实现找基准值 基准值的注释：在快排的过程中，每一次我们要取一个元素作为枢纽值，以这个数字来将序列划分为两部分。 在此我们采用三数取中法，也就是取左端、中间、右端三个数，然后进行排序，将中间数作为枢纽值。 快速排序实现主框架： //快速排序 void QuickSort(int* arr, int left, int rig
阅读更多...
6.1.数据结构-c/c++堆详解下篇（堆排序，TopK问题）

6.1.数据结构-c/c++堆详解下篇（堆排序，TopK问题）

上篇：6.1.数据结构-c/c++模拟实现堆上篇（向下，上调整算法，建堆，增删数据）-CSDN博客 本章重点 1.使用堆来完成堆排序 2.使用堆解决TopK问题 目录 一.堆排序 1.1 思路 1.2 代码 1.3 简单测试 二.TopK问题 2.1 思路(求最小)： 2.2 C语言代码（手写堆） 2.3 C++代码（使用优先级队列 priority_queue）
阅读更多...
c++的初始化列表与const成员

c++的初始化列表与const成员

初始化列表与const成员 const成员 使用const修饰的类、结构、联合的成员变量，在类对象创建完成前一定要初始化。 不能在构造函数中初始化const成员，因为执行构造函数时，类对象已经创建完成，只有类对象创建完成才能调用成员函数，构造函数虽然特殊但也是成员函数。 在定义const成员时进行初始化，该语法只有在C11语法标准下才支持。 初始化列表 在构造函数小括号后面，主要用于给
阅读更多...
顺序表之创建，判满，插入，输出

顺序表之创建，判满，插入，输出

文章目录 🍊自我介绍🍊创建一个空的顺序表，为结构体在堆区分配空间🍊插入数据🍊输出数据🍊判断顺序表是否满了，满了返回值1，否则返回0🍊main函数 你的点赞评论就是对博主最大的鼓励 当然喜欢的小伙伴可以：点赞+关注+评论+收藏（一键四连）哦~ 🍊自我介绍   Hello,大家好，我是小珑也要变强（也是小珑），我是易编程·终身成长社群的一名“创始团队·嘉宾”
阅读更多...
《数据结构（C语言版）第二版》第八章-排序（8.3-交换排序、8.4-选择排序）

《数据结构（C语言版）第二版》第八章-排序（8.3-交换排序、8.4-选择排序）

8.3 交换排序 8.3.1 冒泡排序 【算法特点】 (1) 稳定排序。 (2) 可用于链式存储结构。 (3) 移动记录次数较多，算法平均时间性能比直接插入排序差。当初始记录无序，n较大时， 此算法不宜采用。 #include <stdio.h>#include <stdlib.h>#define MAXSIZE 26typedef int KeyType;typedef char In
阅读更多...
遮罩，在指定元素上进行遮罩

遮罩，在指定元素上进行遮罩

废话不多说，直接上代码： ps:依赖 jquer.js 1.首先，定义一个 Overlay.js  代码如下： /*遮罩 Overlay js 对象*/function Overlay(options){//{targetId:'',viewHtml:'',viewWidth:'',viewHeight:''}try{this.state=false;//遮罩状态 true 激活，f
阅读更多...
学习记录：js算法（二十八）：删除排序链表中的重复元素、删除排序链表中的重复元素II

学习记录：js算法（二十八）：删除排序链表中的重复元素、删除排序链表中的重复元素II

文章目录 删除排序链表中的重复元素我的思路解法一：循环解法二：递归 网上思路 删除排序链表中的重复元素 II我的思路网上思路 总结 删除排序链表中的重复元素 给定一个已排序的链表的头 head ， 删除所有重复的元素，使每个元素只出现一次 。返回 已排序的链表 。 图一 图二 示例 1：（图一）输入：head = [1,1,2]输出：[1,2]示例 2：（图
阅读更多...
web群集--nginx配置文件location匹配符的优先级顺序详解及验证

web群集--nginx配置文件location匹配符的优先级顺序详解及验证

文章目录 前言优先级顺序优先级顺序(详解)1. 精确匹配（Exact Match）2. 正则表达式匹配（Regex Match）3. 前缀匹配（Prefix Match） 匹配规则的综合应用验证优先级 前言 location的作用 在 NGINX 中，location 指令用于定义如何处理特定的请求 URI。由于网站往往需要不同的处理方式来适应各种请求，NGINX 提供了多种匹
阅读更多...
如何恢复回收站中已删除/清空的文件

如何恢复回收站中已删除/清空的文件

回收站清空后如何恢复已删除的文件？是否可以恢复永久删除的文件？或者最糟糕的是，如果文件直接被删除怎么办？本文将向您展示清空回收站后恢复已删除数据的最佳方法。 回收站清空后如何恢复已删除的文件？ “回收站清空后我还能恢复已删除的文件吗？” 答案是肯定的，但是在这种情况下您将需要一个  回收站恢复工具 来从回收站中检索文件： 错误/永久删除回收站或任何数字存储设备中的文件 直接删除的文件/
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2