本文主要是介绍计算几何+2sat:1020T3,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
http://cplusoj.com/d/senior/p/SS231019C
我们进行这样的转化
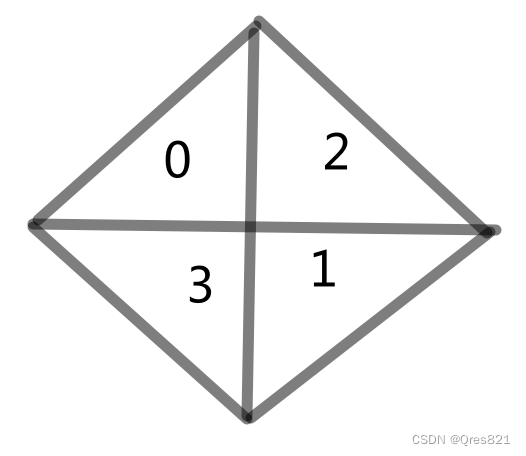
则0/1必选一个,2/3必选一个
那么就变成一个2sat问题
两三角形有交,则一个选,一个不能选
对角三角形一个选,一个不选。一个不选,一个选
三角形不合法,则选向不选连边,代表必须不选
// 5.3k
#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read(){int x=0,f=1;char ch=getchar(); while(ch<'0'||
ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f;}
#define Z(x) (x)*(x)
#define pb push_back
//mt19937 rand(time(0));
//mt19937_64 rand(time(0));
//srand(time(0));
#define N 200010
//#define M
//#define mo
#define eps 1e-4
double H, W, X[N], Y[N];
struct Point {double x, y; Point operator - (const Point &A) const {Point B; B.x=x-A.x; B.y=y-A.y; return B; }double operator ^ (const Point &A) const {return x * A.y - y * A.x; }bool check() {
// printf("Checking %lf %lf\n", x, y); if(x < 0 || x > W) return false; if(y < 0 || y > H) return false; return true; }
};
namespace Cross {bool Line_cross(Point p1, Point p2, Point p3, Point p4) {double a1 = (p1 - p2) ^ (p3 - p2); double a2 = (p1 - p2) ^ (p4 - p2); if(a1 * a2 >= 0) return false; return true; }bool cross(Point p1, Point p2, Point p3, Point p4) {
// printf("(%lf %lf) (%lf %lf) || (%lf %lf) (%lf %lf)\n", p1.x, p1.y, p2.x, p2.y, p3.x, p3.y, p4.x, p4.y); bool t1 = Line_cross(p1, p2, p3, p4); bool t2 = Line_cross(p3, p4, p1, p2); return t1 && t2; }
}
struct node {Point a[3]; void make_node(int i, int j, double k) {a[0] = {X[i], Y[i]}; if(j == 0 || j == 3) a[1] = {X[i], Y[i] + k}; if(j == 3 || j == 1) a[2] = {X[i] + k, Y[i]}; if(j == 1 || j == 2) a[1] = {X[i], Y[i] - k}; if(j == 2 || j == 0) a[2] = {X[i] - k, Y[i]}; }bool check() {if(a[0].check() == false) return false; if(a[1].check() == false) return false; if(a[2].check() == false) return false; return true; }void print() {printf("%lf %lf\n", a[0].x, a[0].y); printf("%lf %lf\n", a[1].x, a[1].y); printf("%lf %lf\n", a[2].x, a[2].y); printf(">> %lld\n", check()); }bool operator ^(const node &A) const {
// ; A.print(); int f0, f1, g0, g1; for(f0 = 0; f0 <= 2; ++f0) for(f1 = f0+1; f1 <= 2; ++f1)for(g0 = 0; g0 <= 2; ++g0)for(g1 = g0+1; g1<=2; ++g1) {if(Cross::cross(a[f0], a[f1], A.a[g0], A.a[g1])) return true; }return false; }}p[N];
int n, m, i, j, k, T;
namespace Graph {int make_node(int i, int j) { return j * n + i; }struct two_sat {int dfn[N], low[N], vis[N], col[N], tot, i; vector<int>G[N]; stack<int>z; void clear() {tot = 0; while(!z.empty()) z.pop(); memset(dfn, 0, sizeof(dfn)); memset(low, 0, sizeof(low)); memset(vis, 0, sizeof(vis)); memset(col, 0, sizeof(col)); for(i=0; i<N; ++i) G[i].clear(); }void add_edge(int u, int v) {
// printf("%lld %lld\n", u, v); G[u].pb(v); }void dfs(int x) {dfn[x] = low[x] = ++tot; z.push(x); vis[x] = 1; for(auto y : G[x]) {if(vis[y] == -1) continue; if(!vis[y]) dfs(y), low[x] = min(low[x], low[y]); else low[x] = min(low[x], low[y]); }
// printf("\t %lld : %lld %lld\n", x, dfn[x], low[x]); if(dfn[x] == low[x]) {while(z.top() != x) col[z.top()] = x, vis[z.top()] = -1, z.pop(); col[x] = x; z.pop(); vis[x] = -1; }
// vis[x] = -1; }void tarjan() {for(i=1; i<=8*n; ++i) if(!vis[i]) dfs(i);
// for(i=1; i<=8*n; ++i) printf("%3lld", i);
// printf("\n");
// for(i=1; i<=8*n; ++i) printf("%3lld", col[i]);
// printf("\n"); }int pan(int u, int v) {return col[u] == col[v]; }}Sat;
}
using namespace Graph;
double l, r, mid, ans; bool check(double k) {
// printf("# Now is %.3lf\n", k); int i, j, x, y, u, v; Sat.clear(); for(i=1; i<=n; ++i) {for(j=0; j<=3; ++j) {u = make_node(i, j); v = make_node(i, j^1); Sat.add_edge(u, v + 4*n); Sat.add_edge(v + 4*n, u ); p[u].make_node(i, j, k);
// p[u].print(); if(p[u].check() == false) Sat.add_edge(u, u + 4*n);
// Sat.add_edge(u + 4*n, u); }
// printf("-----------\n"); }for(i=1; i<=n; ++i) for(j=i+1; j<=n; ++j) for(x=0; x<=3; ++x) for(y=0; y<=3; ++y) {
// if(i == j) continue; u = make_node(i, x); v = make_node(j, y); if(p[u] ^ p[v]) {
// printf("%lld %lld || %lld %lld\n", i, j, x, y); Sat.add_edge(u, v + 4*n); Sat.add_edge(v, u + 4*n); }}Sat.tarjan(); for(i=1; i<=n; ++i) for(j=0; j<=3; ++j) {u = make_node(i, j); v = make_node(i, j^1);
// printf("%lld | %lld %lld %lld\n", i, j, u, u+4*n) ;
// u+4*n, v+4*n); if(Sat.pan(u, u + 4*n)) return false;
// if(Sat.pan(u + 4*n, v + 4*n)) return false; }
// printf("\t ok\n"); return true; }signed main()
{
// freopen("in.txt", "r", stdin);
// freopen("out.txt", "w", stdout);freopen("city.in", "r", stdin);freopen("city.out", "w", stdout);
// T=read();
// while(T--) {
//
// }scanf("%lf%lf%lld", &W, &H, &n); for(i=1; i<=n; ++i) {scanf("%lf%lf", &X[i], &Y[i]); }l = 0; r = max(H, W); while(r - l > eps){mid = (l + r) / 2; if(check(mid)) l = mid, ans = mid; else r = mid; }printf("%.2lf", ans*2); return 0;
}这篇关于计算几何+2sat:1020T3的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







