回转率和上升时间：不完全相同

回转率和上升时间：不完全相同
信号的带宽是多少？，我们看了上升时间和带宽之间的经典关系。

关于上升时间的讨论通常会引出这样的问题：这是否与增长率相同？

让我们看一看斜率，一个类似上升时间的概念，但有一些重要的区别。

如图所示图1，阶跃响应的上升时间定义为波形从最终值的10%过渡到90%所需的时间。(有时使用20/80%来定义上升时间。)

请注意，上升时间定义为波形大小的百分比，并且与所涉及的电压无关。图1中的波形上升时间约为3秒。

图1.步骤响应的上升时间是从最终值的10%过渡到90%所需的时间。

斜率定义为波形的变化率，与斜率相同。它可以使用ΔV/Δt进行计算，如图2.

图2.斜率是波形的斜率，按ΔV/Δt计算。

图2显示了ΔV/Δt在10%和90%点的计算，但计算可以在波形上的任意位置进行。
真的，我们只是在找斜坡。请注意，旋转速率是单位伏特/秒(或更常见的伏特/秒)，这与它是衡量单位时间电压变化多少。

从图2中，我们可以计算出回转率：

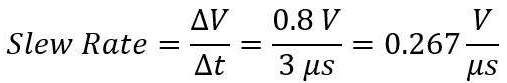
现在想象一下，图2中的阶跃响应是10倍，从零伏特到10伏特，同样的3秒上升时间。回转率计算如下：

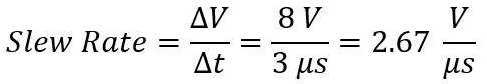
当然，即使上升的时间是相同的，旋转速率是10倍，因为电压变化的速度要高得多。

这突出了上升时间和旋转速率之间的关键区别：上升时间忽略了绝对电压电平，只是表示波形转换所需的时间，而旋转速率则描述电压变化率。

正弦波壳
用于正弦波情况(图3)，我们可以用一些基本的微积分来找出旋转率。

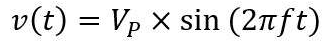
旋转率(SR)是波形的斜率或导数。

当余弦函数达到最大值1时，旋转率将是最大的。当余弦函数达到-1时，也会发生相同的事情，但出现相反的符号。

图3还示出这些最大旋转速率点发生在正弦波的零点交叉处。

不足为奇的是，最大转角率与波形的频率和振幅成正比。更大的波形更快。更高频率的波形也更快。

图3.正弦波在过零点时有最大回转率。

放大器规格
到目前为止，我们一直在讨论电压波形的旋转速率，描述电压变化的速度。

旋转速率用于指定放大器的性能，通常通过定义信号在放大器输出时的速度。这是放大器的最大回转率，这可能是不同的上升斜率和下降斜率波形。

放大器的带宽往往受到旋转速率性能的限制。

全功率带宽(FPBW)又称大信号带宽，是指放大器在最大输出电压波动时产生的最高频率。

假设FPBW受放大器最大回转速率的限制，则可以通过重新排列前一方程来计算FPBW。

应用

回转率是运算放大器的一个重要指标，特别是在处理大的输出波动时。

参考文献2和3是关于旋转速率如何影响运算放大器性能的额外信息的良好来源。

您可能会听到有关电源的讨论，描述电源从一个电压或电流设置到另一个电压或电流设置的速度。

通常这是与可编程电源在一个测试系统中，排序通过不同的测试条件。

电压和电流转速可能是测试刺激的一部分。也就是说，我们可能想要测试一个设备的性能，就像某种电压或电流在两个特定值之间的控制方式。也可以使用旋转速率来控制被测设备的突发性电流。

你也可能遇到旋转速率，因为它涉及电磁干扰(EMI)。边缘锐利的信号倾向于辐射更高频率的内容。

更快的开关电路，如数字逻辑器件和开关电源调节器，因为是EMI的来源而臭名昭著。其中一些设备提供旋转速率控制，允许设计人员选择边缘速度并控制排放。

在其他情况下，可以添加外部电路来减缓边缘。例如，电路设计器可以将RC电路添加到数字时钟电路中，以减少旋转速率和辐射发射。

因此，这是一个简单的概述，转速和上升时间的关系。是的，有相似之处，但关键的区别是旋转率描述了波形的实际变化率。

—Bob Witte is president of Signal Blue LLC, a technology consulting company.

References

Gilbert, Ken, Slew Rate Explained, Dec. 14, 2008.
Basic Linear Design, Hank Zumbahlen, Editor; Chapter 1: The Op Amp, Analog Devices, Inc., 2007.
Trump, Bruce, “Slew Rate—the op amp speed limit,” EDN, June 2, 2013.