量子计算 qiskit_使用Qiskit进行量子误差校正

If you have heard about quantum computers you have likely heard about quantum error correction. If not, Quantum computing is the use of phenomena of quantum mechanics such as superposition, interference, and entanglement to perform computation. This is done via computers known as quantum computers. Now that we have established briefly what a quantum computer is, let’s understand what is quantum error correction?

如果您听说过量子计算机，则可能听说过量子错误校正。 如果不是这样，那么量子计算就是利用诸如叠加 ， 干涉和纠缠之类的量子力学现象来进行计算。 这是通过称为量子计算机的计算机完成的。 既然我们已经简要地确定了什么是量子计算机，让我们了解什么是量子误差校正？

But before we discuss quantum error correction, we should understand what error correction is.

但是在讨论量子纠错之前，我们应该了解什么是纠错。

Due to the current pandemic, many of us would have been in an online meeting on a platform like zoom. Here there could be someone let’s say Alice who might have a bad mic, internet connection, or both for that matter. Alice and Bob are in a zoom meeting, Bob asks Alice do you want pineapple on pizza? Now she says no(like a normal human being, no offense!) but Bob is unable to understand what she is saying.

由于当前的大流行，我们许多人本来可以在Zoom等平台上参加在线会议。 在这里，也许有人说爱丽丝(Alice)的麦克风，互联网连接不良，或两者兼而有之。 爱丽丝和鲍勃正在开会，鲍勃问爱丽丝，你要比萨上的菠萝吗？ 现在她说不(就像正常人一样，没有冒犯！)，但鲍勃无法理解她在说什么。

An easy solution to this problem is to just tell Alice to repeat herself and so he’ll hear mostly ‘no’s with a few random ‘yes’s thrown in. Bob now for sure can say that she said no. This is the basic idea behind repetition codes which is one of the many error correction codes. With this encoding of our message, it has become tolerant of small faults. Here this example contained

解决这个问题的简单方法是，告诉爱丽丝重复自己的话，这样他就会听到大部分都是“否”，并且会随机听到一些“是”。鲍勃现在肯定可以说她拒绝了。 这是重复码背后的基本思想，重复码是许多纠错码之一。 通过我们消息的这种编码，它已经可以容忍小故障。 这里这个例子包含

• Input: Information we have to protect(yes or no for pineapple on pizza).

  输入：我们必须保护的信息(比萨饼上的菠萝是或否)。

• Encoding: Transforming information to make it easier to protect(making Alice repeat herself)

  编码：转换信息以使其更易于保护(使爱丽丝重演)

• Errors: Random perturbations of the encoded message(network issues and bad mic).

  错误：编码消息的随机扰动(网络问题和麦克风故障)。

• Decoding: Working out what the input was(deducing that no was the input by the one which has the highest no of counts)

  解码：算出输入是什么(通过计数最高的那一推论得出输入不是)

The basic idea is that for computation, errors are introduced whenever we operate. We need to keep corrected errors as they are introduced. This can be done by constantly decoding and re-encoding.

基本思想是，为了进行计算，每当我们进行操作时都会引入错误。 在引入错误后，我们需要保持这些错误。 这可以通过不断解码和重新编码来完成。

Readers familiarized with quantum computing can ignore this note.

熟悉量子计算的读者可以忽略此注释 。

Note: From now on there may be some things that some readers who aren’t familiarized with the basics of quantum computing wouldn’t understand for them I will put hyperlinks where they can read those topics in detail. You can also look at the qiskit textbook where these topics would be explained in detail. If you feel like for some topic you need help with please put those concerns in the comments, I’ll edit my article accordingly.

注意：从现在开始，有些事情可能使一些不熟悉量子计算基础知识的读者无法理解，我将在超链接中放置他们可以详细阅读这些主题的地方。 您还可以查看 qiskit教科书 ，其中将详细解释这些主题。 如果您希望在某些主题上需要帮助，请在评论中注明这些问题，我将相应地对其进行编辑。

Unfortunately this method works properly only for bits but not for qubits.

不幸的是，该方法仅适用于位，而不适用于量子位。

Why can’t we do it? Unfortunately due to the no-cloning theorem, we can’t do something like this,

我们为什么不能这样做？ 不幸的是，由于无克隆定理 ，我们不能做这样的事情，

|α>⇏|α>⊗|α>⊗|α>

|α>⇏|α>⊗|α>⊗|α>

Let’s say we wanted to encode some superposition state we can do it this way,

假设我们要编码一些叠加状态，我们可以用这种方式做到这一点，

α|0>+β|1>→ α|000>+β|111>

α| 0> +β| 1>→α| 000> +β| 111>

Now decoding it destroys the superposition state. To solve one issue we have caused another and to solve this issue we need to be more careful with measurement. But wait, what issue are we solving?

现在解码它会破坏叠加状态。 为了解决一个问题，我们已经引起了另一个问题，为了解决这个问题，我们需要在测量时更加小心。 但是等等，我们正在解决什么问题？

Qubits in real life don’t work exactly like the way they should behave as each operation would be slightly wrong, qubits experience something called decoherence (can be viewed as the loss of information from a system into the environment) and measurements can also be incorrect at times.

现实生活中的量子位不能完全按照它们的行为方式工作，因为每个操作都会略有错误，量子位会经历一种称为退相干的现象 (可以视为从系统到环境的信息丢失)，并且测量结果也可能不正确有时。

If we run a circuit in qiskit you can easily see the effect of noise like this

如果我们在qiskit中运行电路，您可以轻松地看到这样的噪声影响

Due to the errors, algorithms like Grover, Shor, Bernstein-Vazirani, etc can’t work properly. Even if you wanted to run an algorithm let’s say Grover’s on those noisy qubits in qiskit you’ll get something like this,

由于这些错误， Grover ， Shor ， Bernstein-Vazirani等算法无法正常工作。 即使您想运行一种算法，假设在qiskit中那些嘈杂的量子位上使用了Grover，您也会得到类似的结果，

As you can see in the case for perfect qubits you can certainly say that the answer would be corresponding to 101 and 110. Whereas in the case of noisy qubits you can’t say for sure what would be the answer for sure. Thus we need qubits that are ideal or at least somewhat close to them. Those qubits are called logical qubits. The downside of that is for every logical qubit we need many physical qubits. Getting even a handful of logical qubits would require hundreds of physical qubits which even the biggest computers don’t have. Therefore using QEC in algorithms is therefore a long-term goal along with those algorithms which require it.

如您所见，对于完美的量子比特，您可以肯定地说答案将与101和110相对应。而对于嘈杂的量子比特，您无法确定答案是肯定的。 因此，我们需要理想的或至少在某些程度上接近它们的量子位。 这些量子位称为逻辑量子位。 不利的一面是，对于每个逻辑量子位，我们都需要许多物理量子位。 要获得几个逻辑量子位，就需要数百个物理量子位，即使最大的计算机也没有。 因此，在算法中使用QEC以及与那些需要它的算法是一个长期目标。

Coming back on being more careful with our measurements. What do even mean by that? The basic idea is that we can extract some sort of information out of those qubits without actually knowing their encoded information. If we just know which values have a different value to the rest than that could also work for us. To do this, we need a qubit for every pair of qubit which is initialized in state |0> and is the target for two CNOT gates. We’ll look at an example of two qubits in qiskit.

回到对我们的测量要更加小心。 那是什么意思呢？ 基本思想是我们可以从那些量子位中提取某种信息，而无需实际知道它们的编码信息。 如果我们只知道哪些价值与其他价值不同，那对我们也可以。 为此，我们需要为每一对在状态| 0>中初始化并且是两个CNOT门的目标的量子位提供一个量子位。 我们来看看qiskit中两个量子比特的例子。

These measurements are repeated throughout computation and are used to identify where errors likely occurred and how to remove their effects. A decoding algorithm(classical) is used for this procedure. With this, we can protect against bit-flip errors(0 flipped to 1) for an arbitrarily long time. This measurement is a syndrome measurement and the result is known as Syndrome. They are ways to check that all the qubits are doing what they should be. They provide clues that allow us to detect and correct errors. Even though their form changes from code to code, but their job is always the same. Thus all codes have them. But how does one even go on decoding them?

这些测量将在整个计算过程中重复进行，并用于识别可能发生错误的位置以及如何消除其影响。 解码算法(经典)用于此过程。 这样，我们可以任意长时间防止位翻转错误(0翻转为1)。 该测量是一种综合症测量 ，其结果称为综合症 。 它们是检查所有量子位是否正在执行应有方式的方法。 它们提供了线索，使我们能够检测和纠正错误。 即使它们的形式在代码之间变化，但它们的工作始终是相同的。 因此，所有代码都有它们。 但是，甚至如何继续解码它们呢？

We’ll look at a very simple case where there are errors between parity measurements only not during any(syndrome measurements are perfect). Here we are at first just trying to identify errors for now but not correcting them. Due to errors, pairs of defects would be created. The one with the highest number of counts will be used to find a minimal pairing.

我们将看一个非常简单的情况，即奇偶校验测量之间只有在任何情况下都不会出现错误(综合征测量是完美的)。 在这里，我们首先只是试图暂时识别错误，而不是纠正它们。 由于错误，将创建成对的缺陷。 计数最高的一个将用于查找最小配对。

Here in the picture, the left side is where errors happen and the right side is where we take into account those errors. Suppose that we have all the qubits initialized to 0. Here in the picture steps are happening in sequence from bottom to top and position are in sequence from left to right. Then we can see in step-1 that positions 3,4 and 4,5 are different so we log those errors as seen in step 1 which can be seen. In step 2 we can see positions 7,8 and 8,9 are different, we’ll log this error in step 2 but not the one in step 1 as can be seen. Step 3 you can see that positions 4 and 5 are now equal, which you think would be a good thing but it is inconsistent with steps seen before. Thus, this happened due to an error and thus we’ll take this also into account as seen in step 3. This process will be repeated several times to get a good idea of those errors.

图片中的左侧是发生错误的位置，右侧是我们考虑到这些错误的位置。 假设我们已将所有量子位初始化为0。在图中，步骤从下到上依次发生，位置从左到右依次发生。 然后我们可以在步骤1中看到位置3,4和4,5不同，因此我们记录了可以在步骤1中看到的那些错误。 在第2步中，我们可以看到位置7,8和8,9不同，我们将在第2步中记录此错误，但在第1步中不会记录该错误。 步骤3您可以看到位置4和5现在相等，您认为这是一件好事，但与之前看到的步骤不一致。 因此，这是由于错误而发生的，因此我们也将考虑到这一点，如步骤3所示。此过程将重复多次，以更好地了解这些错误。

We’ll now look at a somewhat realistic case where syndrome measurements don’t happen perfectly(they will randomly lie). You can see in step 2 that for positions 8 and 9 are different but that isn’t true. Therefore pairing is now a 2D problem, majority voting will not work here.

现在，我们来看一个比较实际的情况，即综合症的测量不能完美地发生(它们会随机说谎)。 您可以在第2步中看到位置8和9不同，但这是不正确的。 因此，配对现在是2D问题，多数表决将无法在此处进行。

One of the best ways to visualize this problem is via graphs, where defects are nodes and the numbers of errors required to link them are weighted edges. A likely set of errors corresponds to the minimum weight perfect matching of the graph.

可视化此问题的最佳方法之一是通过图形，其中缺陷是节点，链接它们所需的错误数是加权边。 可能的一组错误对应于图形的最小权重完美匹配 。

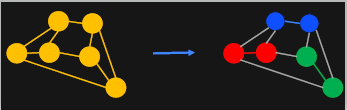
Look at the picture below to understand how does this works. It is clear that first, it said that 0=0 but in the line below it says 0≠0 same is the case for 1 in the first and second line. In the second image below, we visualize these errors according to the procedure described above and come to these results.

查看下面的图片以了解其工作原理。 很明显，首先，它说0 = 0，但在其下面的行中说0≠0，在第一行和第二行中也是如此。 在下面的第二张图像中，我们根据上述过程将这些错误可视化，并得出了这些结果。

Understanding how to manipulate logical qubits is very crucial. This can be done by a logical operation which is made up of many physical operations. For example, doing a logical X is very easy compared to doing logical Ry. For doing Ry gate you have to take the code apart and again put it back together. Now you would remember that when the qubits are not encoded they are not resistant to noise. Things from here get complicated. Therefore the limited set fault-tolerant logical gates is a major problem with the repetition code. Not to forget the code only allows us to detect and correct bit fips, and only bit flips. Even though we made sure it doesn’t cause superpositions to collapse but on the other hand, it doesn’t protect them either. We conclude that the repetition code cannot give us fault-tolerant quantum computation. Question comes to everyone’s mind is that which code gives us fault-tolerant quantum computation then?

了解如何操纵逻辑量子位非常关键。 这可以通过由许多物理操作组成的逻辑操作来完成。 例如，与执行逻辑Ry相比，执行逻辑X非常容易。 为了进行Ry gate，您必须将代码拆开，然后再次将其放回原处。 现在您会记得，当未对量子位进行编码时，它们对噪声没有抵抗力。 这里的事情变得复杂。 因此，有限集合的容错逻辑门是重复代码的主要问题。 别忘了代码只允许我们检测和纠正位错误，并且只有位翻转。 即使我们确保它不会导致叠加崩溃，但另一方面，它也不能保护叠加。 我们得出的结论是，重复代码无法为我们提供容错的量子计算。 每个人都想到一个问题，那就是哪个代码为我们提供了容错量子计算？

The problem with the repetition code is that it treats z basis states very different to x and y basis states.

重复代码的问题在于它对待z基本状态与x和y基本状态非常不同。

To solve these issues we have something called The Surface Code. But what exactly are surface codes?

为了解决这些问题，我们有一种叫做《 The Surface Code》的东西。 但是表面代码到底是什么？

Surface codes are defined 2D lattices of qubits responsible for detecting and correcting errors. They are a family of quantum error-correcting code. We define observables for vertices and the smallest closed-loop, enclosing the region between four lattice sites(plaquettes).

表面代码定义为负责检测和纠正错误的qubits的2D晶格。 它们是量子纠错码家族。 我们定义了顶点的观测值和最小的闭环，将四个晶格位点( plaquettes )之间的区域包围起来 。

Let’s quickly look at plaquette syndrome and vertice syndrome. Plaquette syndrome is similar to the two-qubit measurements in the repetition code, the difference being we measure the parity around plaquettes in the lattice. Which if you recall could be done with CX gates and an extra qubit. Vertex syndrome observables can also be measured using CX gates as an ancilla. Here we look at the |+>and |−>states, and count the parity of the number of |−>s. If you wanna learn more about this you can read this research paper and this video by Andrew Houck.

让我们快速看一下Plaquette综合征和vertice综合征。 Plaquette综合征类似于重复代码中的两个量子位测量，不同之处在于我们测量了晶格中Plaquettes周围的奇偶校验。 如果您还记得，可以使用CX门和一个额外的qubit完成。 顶点综合症可观察到的东西也可以使用CX门作为辅助来测量。 在这里，我们查看| +>和| −>状态，并计算| −> s数量的奇偶校验。 如果您想了解更多有关此内容的信息，可以阅读安德鲁·霍克(Andrew Houck)的研究论文和视频 。

Wrapping things up, we learnt that quantum error correction is the detection of errors caused by noise or decoherence, reconstruction of the input without those errors in a quantum computer. We need quantum error correction as without it most algorithms built for quantum computers wouldn’t work. Limitations of the repetition codes, and thus the need for something like surface codes. I would like to end this article with something truly beautiful James Wootton said,

综上所述，我们了解到，量子错误校正是检测由噪声或退相干引起的错误，在没有量子计算机中的错误的情况下重构输入。 我们需要量子误差校正，因为没有它，大多数为量子计算机构建的算法将无法正常工作。 重复代码的局限性，因此需要类似表面代码的东西。 我想以一个真正美丽的詹姆斯·沃顿(James Wootton)的话结束本文，

It is not good when things are too easy because they are easy for errors too!

如果事情太容易了，那就不好了，因为事情也容易出错！

PS: Many parts of this article are based on notes I created during James Wootton’s lecture where he explained the topics very well to me. I hope that I have done at least half a decent job to you. You can see his thought provoking articles here and again a big thank you to him.

PS：本文的许多部分都是基于我在James Wootton演讲期间创建的注释，他在演讲中向我很好地解释了这些主题。 我希望我至少对你做了半份体面的工作。 您可以 在这里 看到他的发人深省的文章 ， 并再次非常感谢他。