WGS84大地坐标转目标椭球平面坐标完整代码和步骤___含高精度高斯投影(正算)

WGS84大地坐标转目标椭球平面坐标完整代码和步骤___含高精度高斯投影(正算)
最近摸索高精度坐标解算，从WGS84椭球大地坐标转换到目标椭球平面坐标，大都是四步，总结大多公式，如下：

1、从大地坐标转换到空间直角坐标，同椭球，公式基本一致。

VB代码:
Dim e2 As Double, N As Double
e2 = 1 - (1 - 1 / f) ^ 2 
N = a / Sqr(1 - e2 * Sin(B) ^ 2) '卯酉圈的曲率半径
X = (N + H) * Cos(B) * Cos(L)
Y = (N+ H) * Cos(B) * Sin(L)
Z = (N * (1 - e2) + H) * Sin(B)
'a为源椭球长半轴，1/f为源椭球扁率，e2为源椭球第一偏心率平方，B为GPS纬度，L为GPS经度，H为GPS海拔

2、从源空间直角坐标转换到目标空间直角坐标，异椭球，公式基本一致（七参数或三参数转换）。

VB代码:
X = dX + (1 + K * 0.000001) * X + wZ * Y - wY * Z
Y = dY + (1 + K * 0.000001) * Y - wZ * x + wX * Z
Z = dZ + (1 + K * 0.000001) * Z + Y * x - wX * Y
'dX、dY、dZ、wX、wY、wZ、K为七参数系数

3、从目标空间坐标转换到目标大地坐标，同椭球，公式基本一致。根据空间坐标，应用回归方程计算平面坐标。

VB代码:
L = Atn(Y/X)
B = 0
Dim CalcLat As Double '计算纬度
Dim N As Double，e2 As Double
e2 = 1 - (1 - 1 / f) ^ 2 
Do '回归计算纬度CalcLat = BN = a / Sqr(1 - e2 * Sin(B) ^ 2) '卯酉圈的曲率半径B = Atn(Z + N * e2 * Sin(CalcLat) / Sqr(X ^ 2 + Y ^ 2))
Loop While Abs(B - CalcLat) > 0.00000000000001If Lon < 0 ThenLon = Lon + Pi
End If
N = a / Sqr(1 - e2 * Sin(B) ^ 2)  '卯酉圈的曲率半径
H = Sqr(X ^ 2 + Y ^ 2)  / Cos(B) - N
'X、Y、Z为空间坐标，a为目标椭球长半轴，1/f为目标椭球扁率，e2为目标椭球第一偏心率平方

4、从目标大地坐标转换到目标平面坐标，同椭球，俗称投影，我国一般采用高斯投影，坐标转换计算的精度，关键在于投影的展开精度。

高精度高斯投影(正算)，适应所有椭球，VB代码，通过计算验证，精度高，达到微米级，亲测代码非常可靠：

高精度高斯投影(正算)，适应所有椭球，C#代码，通过计算验证，精度高，达到微米级，亲测代码非常可靠：

5、最后是一个WGS84椭球转目标平面坐标的简易集成模块，一个模块一步到位，合并所有步骤，通过代码优化，精度可以达到0.001米，毫米级，亲测代码可靠：

莫洛登斯基椭球转换和简易高斯投影。为简洁代码，使用参数类，EllipsoidParam 为自定义椭球参数类，SevenParam 为自定义七参数类，VB代码:

6、程序中关于椭球的定义和常用公式，其中很多参数与公式，参照EXCEL坐标高精度转换，如下详图介绍：

以上代码只要在单元格中加入另外4个参数的单元格，即可支持七参数。
在这里完善命令即可：
Private Sub CommandButton1_Click() '完整布尔莎七参数和简易布尔莎七参数转换,高斯投影
…
…
dx = Val(Range(“G2”)) '七参数
dy = Val(Range(“G3”))
dz = Val(Range(“G4”))
wx = Val(Range(“H2”))
wy = Val(Range(“H3”))
wz = Val(Range(“H4”))
K = Val(Range(“H5”))

ConvertSevenParam.dx = dx
ConvertSevenParam.dy = dy
ConvertSevenParam.dz = dz
ConvertSevenParam.wx = wx
ConvertSevenParam.wy = wy
ConvertSevenParam.wz = wz
ConvertSevenParam.K = K

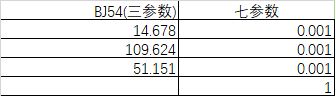
初学者看代码要多研究、多测试。