本文主要是介绍BP神经网络温度补偿器设计,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
背景
设计一个具有温度自补偿功能的二传感器数据融合智能传感器系统,其结构如图:
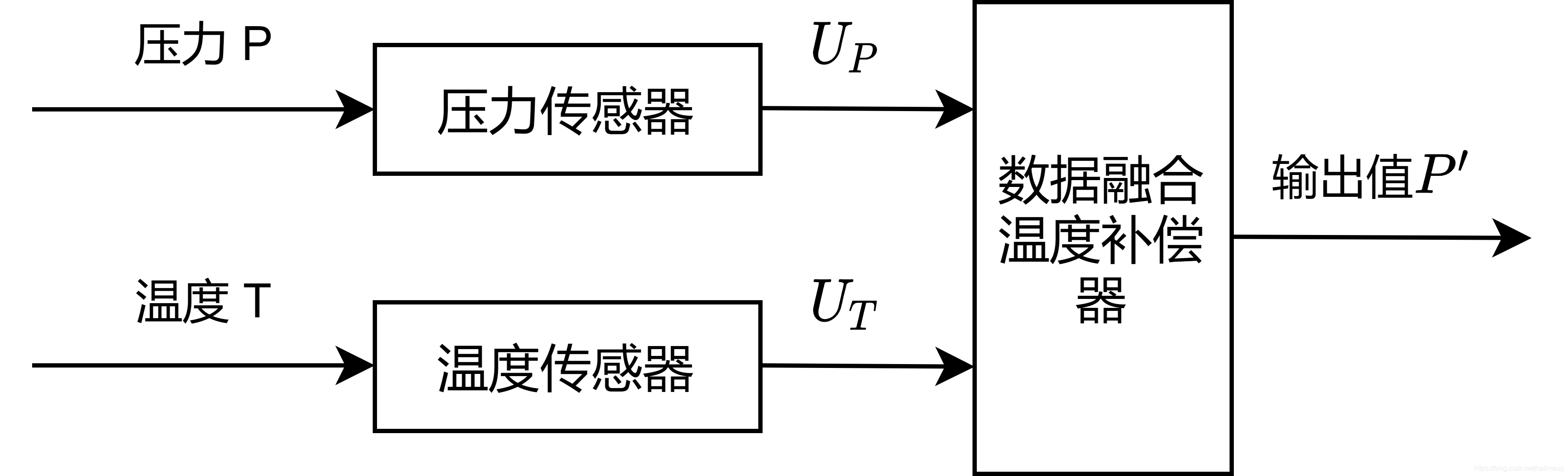
被补偿的主传感器是压阻式压力传感器,输出值为代表压力的电信号 U P U_P UP,辅助传感器用于监测工作环境的干扰温度T,输出值为 U T U_T UT, U P U_P UP和 U T U_T UT输入到融合补偿器中,补偿器根据两者的数据综合考虑,输出当前的压力值 p ′ p' p′.本实验要求将补偿器设计成神经网络结构,并将给定的36个数据分为训练集和测试集,进行网络的训练和效果测试。
36组数据见表:
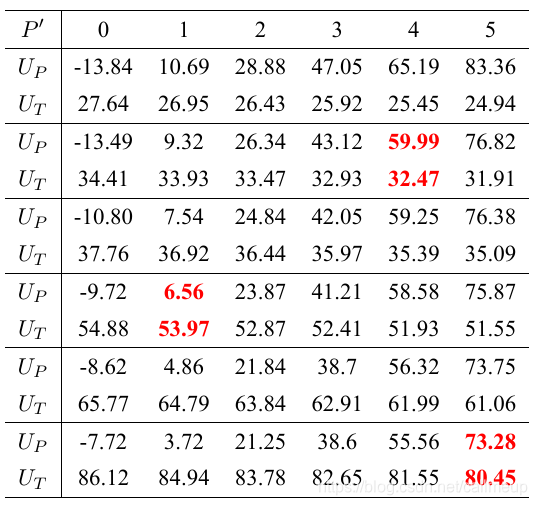
预期功能
- 温度补偿功能: 可对传感器进行温度补偿;
- 可更换学习样本进行再训练:适应不同压力量程的传感器 在不同工作环境温度影响下进行温度补偿;
- 可输出进行了零点及非线性补偿的压力值:网络训练完毕后,输入压力传感器量程范围内的任何 U P U_P UP与 U T U_T UT, 补偿模块可给出在消除温度影响的同时也进行了零点及非线性补偿的压力值 P ′ P′ P′。
设计要求
- 写出BPNN(BP神经网络)温度补偿器的matlab代码
- 评价压力传感器配备了BPNN温度补偿器后的性能
实验分析
网络分析
将表数据集中36组数据随机抽取3个作为测试集(已在表中用加粗、标红),其余33组数据作为训练集。由题意,神经网络的输入层设置2个单输入、7输出的神经元组,输入与输出相等,即权重为1,阈值为0,使用 s i g n sign sign函数进行激发。中间层设置7个神经元,输出层为一个7输入单输出的神经元,网络构成如图所示的结构:
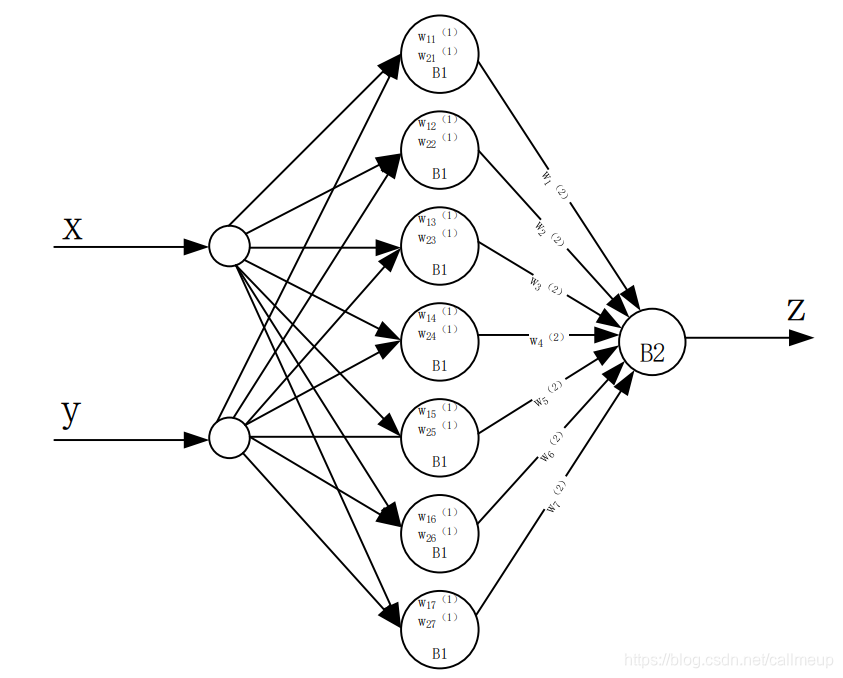
由图示可以分析出中间层神经元输入有7个权重,即: w 11 ( 1 ) , w 12 ( 1 ) , w 13 ( 1 ) , w 14 ( 1 ) , w 15 ( 1 ) , w 16 ( 1 ) , w 17 ( 1 ) ; w 21 ( 1 ) , w 22 ( 1 ) , w 23 ( 1 ) , w 24 ( 1 ) , w 25 ( 1 ) , w 26 ( 1 ) , w 27 ( 1 ) w_{11}^{(1)},w_{12}^{(1)},w_{13}^{(1)}, w_{14}^{(1)},w_{15}^{(1)},w_{16}^{(1)},w_{17}^{(1)}; w_{21}^{(1)},w_{22}^{(1)},w_{23}^{(1)},w_{24}^{(1)},w_{25}^{(1)},w_{26}^{(1)},w_{27}^{(1)} w11(1),w12(1),w13(1),w14(1),w15(1),w16(1),w17(1);w21(1),w22(1),w23(1),w24(1),w25(1),w26(1),w27(1)
阈值定义为 B 1 B1 B1,是一个数组,维数为7。输出层为一个7输入单输出的神经元,输入有7个权重,即 w 1 ( 2 ) , w 2 ( 2 ) , w 3 ( 2 ) , w 4 ( 2 ) , w 5 ( 2 ) , w 6 ( 2 ) , w 7 ( 2 ) w_{1}^{(2)},w_{2}^{(2)},w_{3}^{(2)},w_{4}^{(2)},w_{5}^{(2)},w_{6}^{(2)},w_{7}^{(2)} w1(2),w2(2),w3(2),w4(2),w5(2),w6(2),w7(2),阈值定义为 B 2 B2 B2,是一个数。
对于输入层,输入即为输出。
对于隐层,输入 h i d e _ i n = x ⋅ w − b hide\_in=x\cdot w-b hide_in=x⋅w−b,输出 h i d e _ o u t = f ( h i d e _ i n ) hide\_out=f(hide\_in) hide_out=f(hide_in)其中 f f f为激发函数,在选择上具有一定的随机性,选择S型函数 S i g m o i d Sigmoid Sigmoid作为激发函数,因为S型函数具有输出范围有限、易于求导等特点,计算量小,结果不易发散,且编程简单。所以:

对于输出层,只有一个7输入、单输出的神经元,将权重表示为向量形式 W 2 ( 7 × 1 ) W2_{(7\times 1)} W2(7×1),则 y _ o u t = h i d e _ o u t ( 1 × 7 ) ⋅ W 2 ( 7 × 1 ) − B 2 ( 1 × 1 ) y\_out = hide\_out_{(1\times 7)}\cdot W2_{(7\times 1)}- B2_{(1\times 1)} y_out=hide_out(1×7)⋅W2(7×1)−B2(1×1).
归一化处理
归一化是神经网络里面经常用到的方法,用来给数据进行预处理,可以使网络快速收敛、样本数据量纲化,从而统一评价标准,防止采用sigmoid转移函数时引起的神经元输出饱和。本实验的双输入有一个特性,即两个输入总是成对的,所以虽然输入为2个33维的数据集,但是在训练时并不需要将其两两组合再带入,而是将其配套组合成33组后带入即可。归一化处理后的数据在-1+1或者01之间,此处将数据归一化在 − 1 ∼ 1 -1 \sim 1 −1∼1之间,归一化公式为:
X ˉ = X − X min X max − X min \bar{X}=\frac{X-X_{\min }}{X_{\max }-X_{\min }} Xˉ=Xmax−XminX−Xmin
误差
误差计算公式为: e = z _ o u t − z [ i ] e = z\_out - z[i] e=z_out−z[i],其中 y [ i ] y[i] y[i]为每个训练样本的实际值。
反向修正
神经网络的一大特点即为可以反复修正,通过误差的大小自动调整拟合模型,最终无限接近于样本。
训练的目标为各个输入的权重和神经元的阈值。首先按照式\ref{单输入最后一层修正}从输出层开始修正,其中:
d B 2 = − t h r e s h o l d ⋅ e d W 2 = e ⋅ t h r e s h o l d ⋅ h i d e _ o u t \begin{array}{l} dB2 = -threshold \cdot e \\ dW2 = e \cdot threshold \cdot hide\_out \end{array} dB2=−threshold⋅edW2=e⋅threshold⋅hide_out
最后修正中间层(输入层没有可改变的权重与阈值,所以不需要修正),如式: d B 1 = W 2 ⋅ s i g m o i d ( h i d e _ i n ) ⋅ ( 1 − s i g m o i d ( h i d e _ i n ) ) ⋅ − e ⋅ t h r e s h o l d d W 1 = W 2 ⋅ s i g m o i d ( h i d e _ i n ) ⋅ ( 1 − s i g m o i d ( h i d e _ i n ) ) ⋅ x ⋅ e ⋅ t h r e s h o l d \begin{array}{c} dB1 = W2 \cdot sigmoid(hide\_in)\cdot (1 - sigmoid(hide\_in)) \cdot -e \cdot threshold \\ dW1 = W2 \cdot sigmoid(hide\_in)\cdot (1 - sigmoid(hide\_in)) \cdot x \cdot e \cdot threshold \end{array} dB1=W2⋅sigmoid(hide_in)⋅(1−sigmoid(hide_in))⋅−e⋅thresholddW1=W2⋅sigmoid(hide_in)⋅(1−sigmoid(hide_in))⋅x⋅e⋅threshold
其中, s i g m o i d ( h i d e _ i n ) ⋅ ( 1 − s i g m o i d ( h i d e _ i n ) ) sigmoid(hide\_in)\cdot (1 - sigmoid(hide\_in)) sigmoid(hide_in)⋅(1−sigmoid(hide_in))为 s i g m o i d ( h i d e _ i n ) sigmoid(hide\_in) sigmoid(hide_in)的导数。
最后将用W和B减去对应的改变值dW和dB,即可得到新的权值和阈值,由循环语句进行循环迭代即可,如式::
W 1 = W 1 − d W 1 B 1 = B 1 − d B 1 W 2 = W 2 − d W 2 B 2 = B 2 − d B 2 \begin{array}{c} W1 = W1 - dW1\\ B1 = B1 - dB1\\ W2 = W2 - dW2\\ B2 = B2 - dB2\\ \end{array} W1=W1−dW1B1=B1−dB1W2=W2−dW2B2=B2−dB2
实验过程
训练
隐层神经元数量为7个,迭代次数200,学习速率0.007时,总训练误差为3.44.此误差较高,尝试使用增加隐层神经元数量的方法,将隐层神经元数量增加为15个,重新训练,得到的总误差为1.644.绘制迭代的代数与总误差的曲线图,如图:
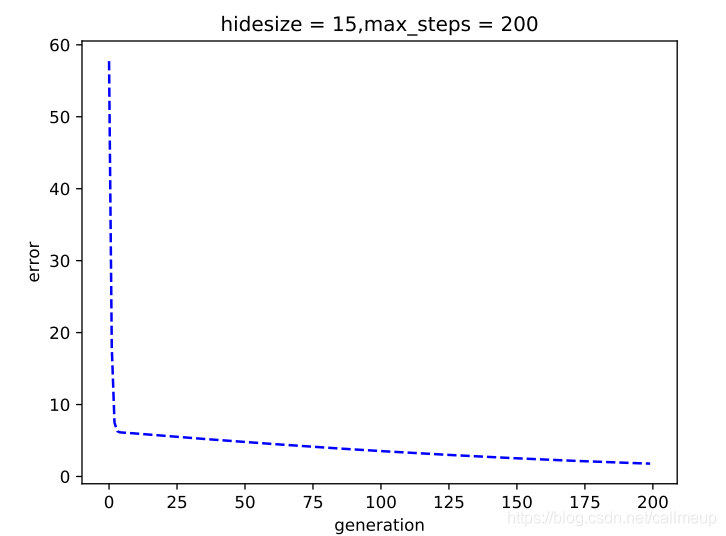
由图像可以发现,在训练的前2-3代,误差迅速降低,继而变成缓慢而均匀地下降,但是始终没有趋于水平,这在优化思想上是没有趋于最优解的,此时如果将迭代的次数增加,基本会有理想的收获。
将迭代次数从200次增加至1000次,再次运行程序。总误差约为0.67,绘制迭代的代数与总误差的曲线图,如图:
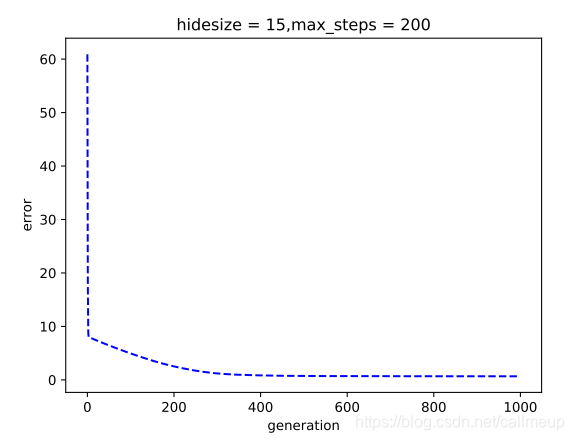
果然,从图像中可以看出,在350代附近时误差几乎不再减少,网络已经训练到此模型下的最优形式。
测试
将剩余的3组测试数据带入训练好的模型进行计算,得到的数据如表\ref{test}.对于此训练集,总误差为0.0212,系统对数据的拟合程度较高。
| 值 | 第一个点 | 第二个点 | 第三个点 |
|---|---|---|---|
| 真实值 | 4 | 1 | 5 |
| 计算值 | 3.98944078 | 0.99795465 | 4.85474882 |
| 偏差 | 0.011 | 0.002 | 0.145 |
总结
本次作业利用神经网络进行传感器融合-温度补偿实验,学习了神经网络建立、校正等知识。实验很成功,但是在反馈方式等方面理论知识依然不足,一直在使用最小二乘法进行校正,如果换用其他方法,同时调整校正速度,有可能会获取更好的拟合效果与收敛速度。
程序
关于本实验的python程序,见:链接。如有疑问,请联系evandjiang@qq.com
这篇关于BP神经网络温度补偿器设计的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








