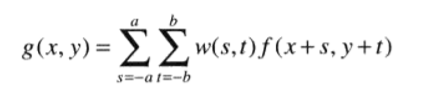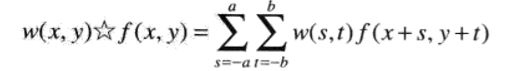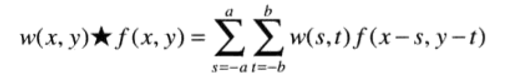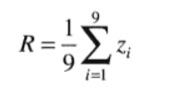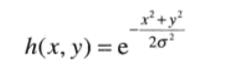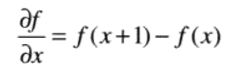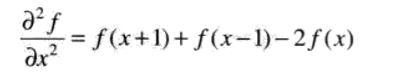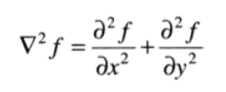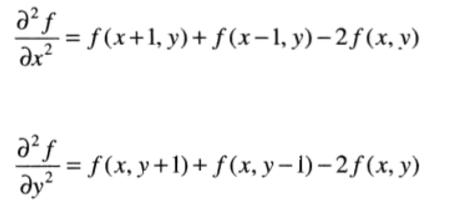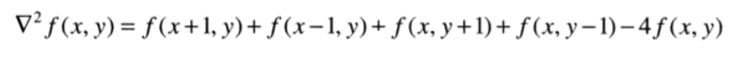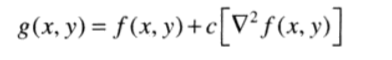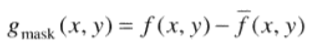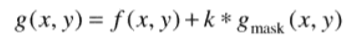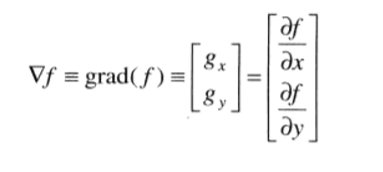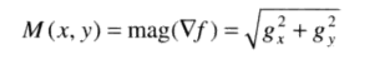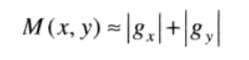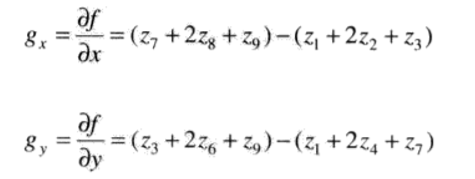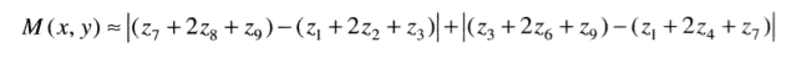本文主要是介绍冈萨雷斯数字图像处理-数字图像基础(Matlab)-图像的空间滤波,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
本小节,我们主要介绍图像的空间滤波及其应用,并用Matlab对其进行实现。
空间滤波的机理
空间滤波是指在某个像素的邻域中对该像素进行预定义操作的过程。如果该操作是线性的,我们称该滤波器为线性空间滤波器,否则为非线性空间滤波器。
首先我们重点关注线性滤波器,一般而言,对于一个M×N的图像采用大小为m×n的滤波器进行空间滤波,可以表示为:
其中x,y表示图像中的某个像素,一般而言这里的m和n均为奇数,这里令m=2a+1,n=2b+1。
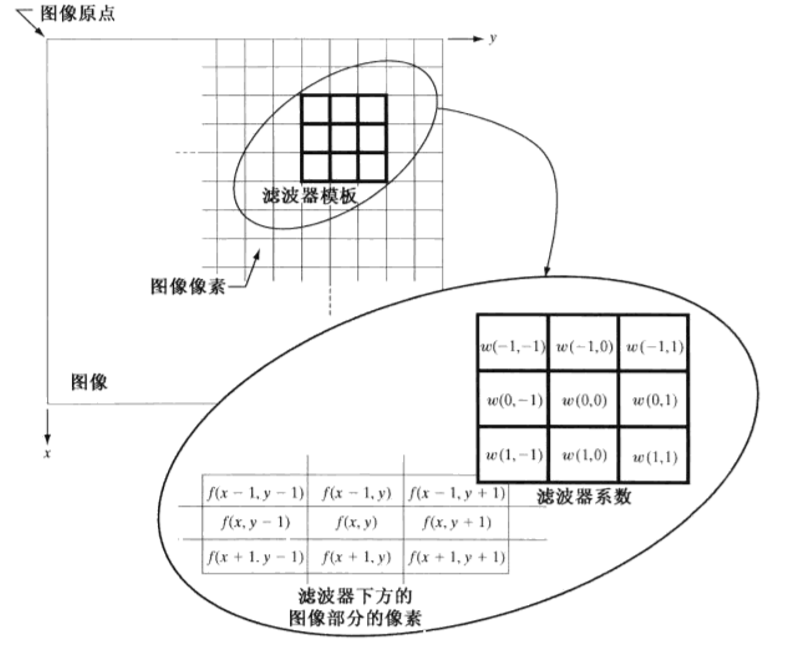
我们可以用下图示例:
空间相关与卷积
空间相关是指滤波器模板移过图像并计算每个位置乘积之和的处理。
空间卷积与空间相关类似,先将滤波器旋转180°,再进行空间相关就是空间卷积。
常用的两个空间滤波器模板是均值滤波器:
以及高斯滤波器:
平滑空间滤波器
平滑滤波器常用于模糊处理和降噪。模糊处理常常用于预处理,以剔除图像中的一些琐碎细节或噪声。
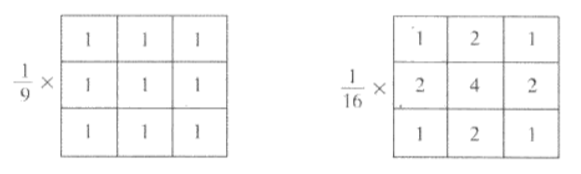
平滑滤波器的一个典型示例是均值滤波器,它使用滤波器模板确定的邻域内像素的平均灰度值代替图像中的像素,这种处理结果降低了图像灰度的“尖锐”变化,属于低通滤波器。下图是均值滤波器常用模板,第一个为平均值滤波器模板,第二个为加权平均滤波模板。
下面以字母a分别以尺寸为3,5,9,15像素的方形均值滤波器得到的相应平滑结果。下面是相应的matlab代码。
这里应用到imfilter滤波器。
clear
clc
photo=imread('字母a.jpg');
m=15;
n=15;
w=ones(m,n)/(m*n);img1=imfilter(mat2gray(photo),w,'conv','replicate','same');
img1=im2uint8(img1);
figure(1)
imshow(photo);
title('原图像')
figure(2)
imshow(img1);
title({['m=',num2str(m),'的方形均值滤波模板平滑处理结果图']})





m=5时的结果基本相似,但模糊程度稍微有所增加。在m=9时,可以明显看到图像更加模糊。对于m=15来说,已属于极端情况。可以看到图像中的一部分小方框和小圆圈以及噪声矩形区域已不断融入背景中。
下面我们以哈勃望远镜得到的图像进行处理。
clear
clc
photo=imread('来自哈勃望远镜图像.jpg');
m=15;
n=15;
w=ones(m,n)/(m*n);
photo=rgb2gray(photo);img1=imfilter(mat2gray(photo),w,'conv','replicate','same');
img1=im2uint8(img1);
figure(1)
imshow(photo);
title('原图像')
figure(2)
imshow(img1);
title({['m=',num2str(m),'的方形均值滤波模板平滑处理结果图']})img2=img1;
img1max=max(max(img2));img2(img2<=img1max*0.25)=0;
img2(img2>img1max*0.25)=255;
figure(3)
imshow(img2);
title('使用阈值处理后的结果')


统计排序(非线性)滤波器
统计排序滤波器是一种非线性滤波器。其思路是将以滤波器包围的图像区域中所包含的像素的排序为基础,然后使用统计排序的结果来替代中心像素的值。常用的统计量有中值、最大值和最小值。其中最知名的是中值滤波器,中值滤波器对处理脉冲噪声非常有效,该噪声也成为椒盐噪声。例如下图为被椒盐噪声污染的电路板X射线图像。
我们首先利用3×3均值模板进行处理,我们发现均值滤波器模糊了图像,而且噪声去除性也很差。
clear
clc
photo=imread('电路板.jpg');
m=3;
n=3;
w=ones(m,n)/(m*n);
number=(m*n+1)/2;
photo=rgb2gray(photo);img1=imfilter(mat2gray(photo),w,'conv','replicate','same');
img1=im2uint8(img1);
figure(1)
imshow(photo);
title('原图像')
figure(2)
imshow(img1);
title({['m=',num2str(m),'的方形均值滤波模板平滑处理结果图']})现在我们利用中值滤波进行处理。这里利用到排序滤波器函数ordfilt2.
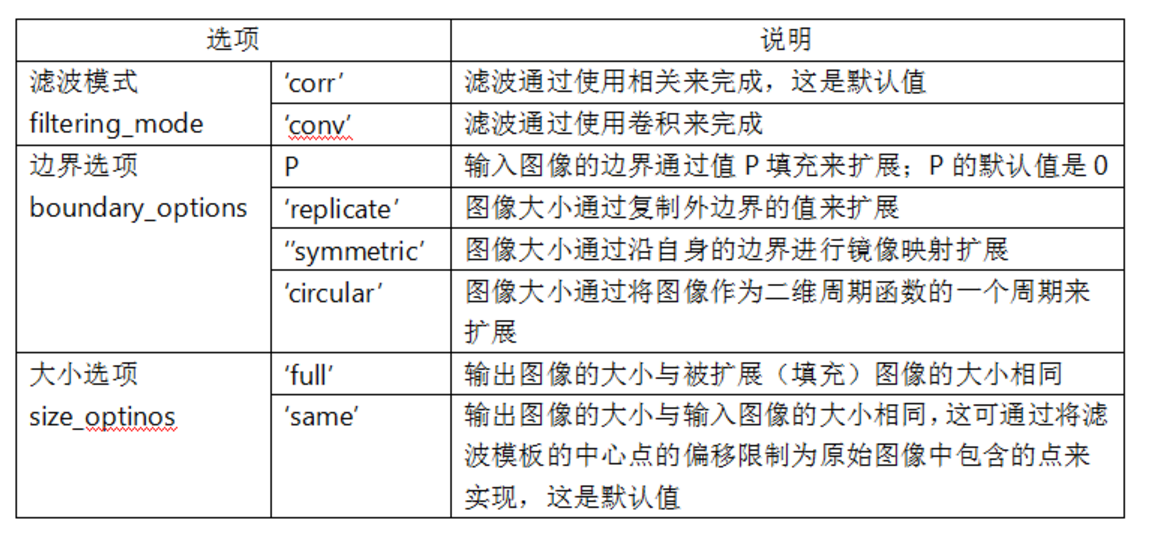
ordfilt2函数语法格式为:
B=ordfilt2(A,order,domain)
B=ordfilt2(A,order,domain,S)
B=ordfilt2(...,padopt)
第一种格式的功能是:对图像A作顺序统计滤波。参数A为输入图像矩阵,order为序号,domain为滤波窗口。即对图像A中大小为domain矩阵大小内的非零像素值进行升序排序,取第order个值作为输出像素值。
第二种格式的功能是:对图像A作顺序统计滤波,前面3个参数与第一种格式相同。S是与domain大小相同的矩阵,它的每一个元素值对应domain中非零值位置的加性偏置输出。
第三种格式的功能是:对图像A作顺序统计滤波,前面省略号代表上面二种格式的一种参数形式。padopt是控制图像A矩阵边界填充的形式,padopt默认设置为'zeros',边界被填充为0像素值,设置为'symmetric'时,A对称地扩展边界。
这里我们设置为:对原图像photo进行处理,在w模板中(可以直接设置为ones(3,3),表示在大小为3×3的邻域矩阵中),获取第number个数,这里的number为中位数等于5。
img2=ordfilt2(photo,number,w);
figure(3)
imshow(img2);
title('中值滤波后的图像')
锐化空间滤波器
锐化空间滤波器主要目的是突出灰度的过渡部分。我们利用数学微分的方法来增强图像边缘和其他突变(如噪声),从而削弱灰度变化缓慢的区域。其属于高通滤波器。
我们定义函数的微分为:
对于一阶微分:(1)在恒定灰度区域的微分值为零。(2)在灰度台阶或斜坡处微分值非零。(3)沿斜坡的微分值非零。
对于二阶微分:(1)在恒定灰度区域的微分值为零。(2)在灰度台阶或斜坡处微分值非零。(3)沿斜坡的微分值为零。
由于我们处理的是数字量,其值有限,因此最大灰度级变化也是有限的,并且变化发生的最短距离是在两相邻像素之间。因此图像的一阶微分和二阶微分均是有界的。
这里我们定义一维离散函数的一阶微分为:
二阶微分为:
对于数字图像,其图像边缘在灰度上常常类似于斜坡过渡,而一阶微分在斜坡中非零,二阶微分为零,这就导致图像的一阶微分产生较粗的边缘,二阶微分产生由零分开的一个像素宽的双边缘。由此,我们可以得出结论,二阶微分在增强细节方面要比一阶微分好得多。
使用二阶微分进行图像锐化----拉普拉斯算子
一个二维图像的拉普拉斯算子定义为:
其中:
因此,拉普拉斯算子可以表示为:
拉普拉斯是一种微分算子,其可以强调图像中灰度的突变,并不强调灰度级缓慢变换的区域。我们可以将原图像和拉普拉斯图像叠加到一起,就可以复原背景特性并保持拉普拉斯锐化处理的效果。
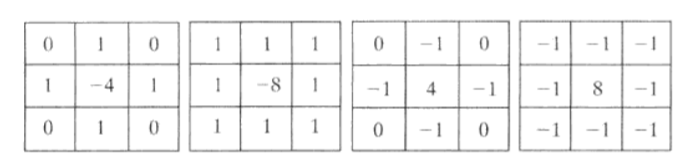
下面是常用的拉普拉斯锐化模板。
其中左1为上述公式的滤波器模板,左2为带有对角项的该公式的扩展模板,左3和左4为其负数项。因此当选用前两个模板时,c=-1;选用后两个模板时,c=1。
下面是月球北极的模糊图像。
我们首先对该图使用拉普拉斯模板,由于拉普拉斯既有正值又有负值,因此我们需要对其进行标定,因此背景大部分为黑色。
clear
clc
photo=imread('月球北极的模糊图像.jpg');
m=3;
n=3;
w1=[0,1,0;1,-4,1;0,1,0];
w2=[1,1,1;1,-8,1;1,1,1];
photo=rgb2gray(photo);img1=imfilter(mat2gray(photo),w1,'conv','replicate','same');
img1=im2uint8(img1);
figure(1)
imshow(photo);
title('原图像')
figure(2)
imshow(img1);
title('标定的拉普拉斯滤波后的图像')
img2=photo-img1;
figure(3)
imshow(img2);
title('用a中的模板锐化后的图像')img3=imfilter(mat2gray(photo),w2,'conv','replicate','same');
img3=im2uint8(img3);
img4=photo-img3;figure(4)
imshow(img4);
title('用b中的模板锐化后的图像')

我们可以看到,经拉普拉斯锐化后的图像,增强了图像中灰度突变出的对比度,使图像中的细节部分得到了增强,并良好地保留了图像的背景色调。而最后一张图采用对角线扩展模板,使图像在对角方向产生了额外的锐化。
非锐化遮蔽和高提升滤波
非锐化遮蔽的过程可以表示为:
(1)模糊原图像
(2)从原图像中减去模糊图像(产生的差值图像称为模板)
(3)将模板加到原图像上
用公式可以表示为:
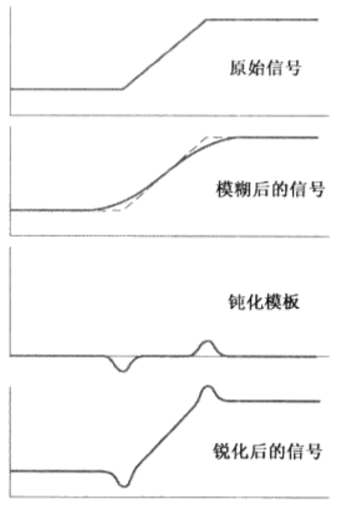
其中,k为权重系数,当k=1时,我们称该过程为非锐化遮蔽,当k>1时,该处理过程称为高提升滤波,当0<k<1时则不强调非锐化模板的贡献。下图为非锐化遮蔽的示意图。
下面我们对一幅在暗灰背景上稍微有点模糊的白文本图像进行处理。
首先我们进行高斯滤波,并得到非锐化遮蔽模板。这里应用fspecial产生高斯滤波器。
h = fspecial(type)
h = fspecial(type,parameters,sigma)
参数type制定算子类型,parameters指定相应的参数,具体格式为:
type='average',为均值滤波,参数为n,代表模版尺寸,用向量表示,默认值为[3,3]。
type= 'gaussian',为高斯低通滤波器,参数有两个,n表示模版尺寸,默认值为[3,3],sigma表示滤波器的标准差,单位为像素,默认值为
0.5。
type= 'laplacian',为拉普拉斯算子,参数为alpha,用于控制拉普拉斯算子的形状,取值范围为[0,1],默认值为0.2。
type= 'log',为拉普拉斯高斯算子,参数有两个,n表示模版尺寸,默认值为[3,3],sigma为滤波器的标准差,单位为像素,默认值为0.5
type= 'prewitt',为prewitt算子,用于边缘增强,无参数。
type= 'sobel',为著名的sobel算子,用于边缘提取,无参数。
type= 'unsharp',为对比度增强滤波器,参数alpha用于控制滤波器的形状,范围为[0,1],默认值为0.2。
这里我们选用gaussian,大小为5×5,方差为3。为方便显示,非锐化模板进行了标定。
clear
clc
photo=imread('DIPXE.jpg');
m=5;
n=5;
sig=3;
w=fspecial('gaussian',[m n],sig);
photo=rgb2gray(photo);
img1=imfilter(photo,w,'conv','replicate','same');
img1=im2uint8(img1);
figure(1)
imshow(photo);
title('原图像')
figure(2)
imshow(img1);
title('使用高斯滤波器模糊的结果')
img2=photo-img1;
img22=im2uint8(mat2gray(photo-img1));
figure(3)
imshow(img22);
title('非锐化模板')
下面进行相加处理得到非锐化遮蔽和高提升滤波的结果,由于高滤波提升引入了部分脉冲噪声,这里最后使用中值滤波过滤。
img3=photo+1*img2;
figure(4)
imshow(img3);
title('使用非锐化掩蔽的结果')img4=photo+4.5*img2;
figure(5)
imshow(img4);
title('使用高提升滤波的结果')w=ones(3,3)/(3*3);
photo=img4;
img5=ordfilt2(photo,5,w);
figure(6)
imshow(img5);
title('使用中值滤波的结果')

可以看到最后处理的结果比原图像由重大改进。
使用一阶微分(非线性)对图像锐化----梯度
图像处理中的一阶微分是用梯度幅值来实现的,梯度可以定义为:
该向量的幅度值可以表示为:
然而该向量的幅度不是线性算子,因为求幅度是做平方和平方根的操作。另一方面,梯度向量的幅度是旋转不变的,因此,在某些实现中,用绝对值来近似处理。
然而该表达式虽然保留了灰度的相对变化,但是各向同性的特性丢失了。为满足一阶微分的定义,Roberts在1965年提出两个定义使用交叉差分的方式进行处理,最终可以表示为:
将上式代入,得到Sobel算子:
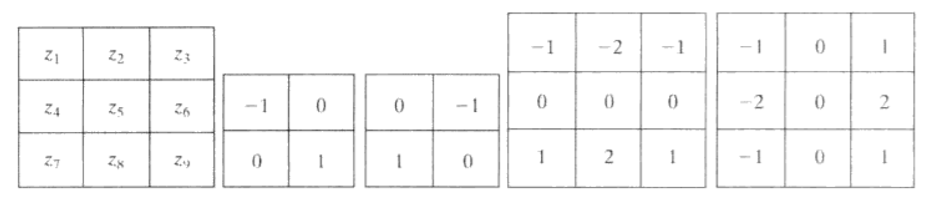
下面是其梯度算子模板:
左1为一幅图像的3×3区域,左2和左3为罗伯特交叉梯度算子。左4和左5为Sobel算子。注意,这里的模板中的系数和为0,正如微分算则的期望值那样,表明灰度恒定区域的响应为0.
下面我们对一张隐形眼镜的光学图像(注意4点钟和5点钟方向边界中的缺陷)。
clear
clc
photo=imread('隐形眼镜的光学图像.jpg');
m=3;
n=3;
w1=[-1,-2,-1;0,0,0;1,2,1];
w2=[-1,0,1;-2,0,2;-1,0,1];
photo=rgb2gray(photo);img1=imfilter(mat2gray(photo),w1,'conv','replicate','same');
img1=im2uint8(img1);
figure(1)
imshow(photo);
title('隐形眼镜的光学图像')img2=imfilter(mat2gray(photo),w2,'conv','replicate','same');
img2=im2uint8(img2);img3=im2uint8(mat2gray(img1+img2));
figure(2)
imshow(img3);
title('Sobel梯度')

上述图像显示了使用Sobel模板得到的梯度图像。在该图像中,边缘缺陷清晰可见,同时灰度不变或变化缓慢的图案阴影被去除了,从而简化了自动检测所要求的计算任务。
混合空间增强法
通常,为了达到令人满意的结果,我们往往对给定的任务应用多种互补的图像增强技术。
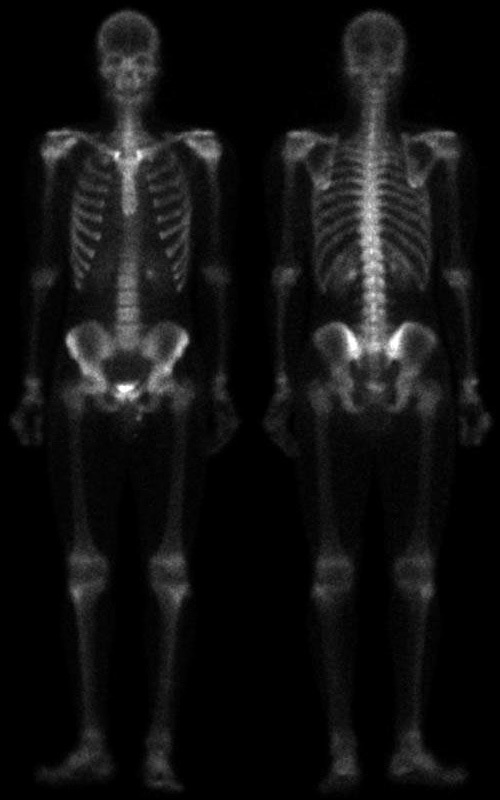
如下图所示为一幅人体骨骼核扫描图像,常常用于检查人体疾病,如骨骼感染和肿瘤。我们的目的是通过图像锐化图出骨骼的更多细节来增强图像。由于图像灰度的动态范围很窄并且由很高的噪声内容,所以很难对其进行增强。对此我们采取的策略是:首先用拉普拉斯法图出图像中的小细节,然后用梯度法图出其边缘。平滑过的梯度图像用于遮蔽拉普拉斯图像。最后,使用灰度变换来增大图像的灰度动态范围。
首先我们对原图像进行拉普拉斯处理:
clear
clc
photo=imread('全身骨骼扫描图像.jpg');
photo=rgb2gray(photo);%%拉普拉斯操作w1=[-1,-1,-1;-1,8,-1;-1,-1,-1]; %拉普拉斯模板
img1=imfilter(photo,w1,'conv','replicate','same');figure(1)
imshow(photo);
title('全身骨骼扫描图像')
figure(2)
imshow(img1);
title('拉普拉斯模板')
然后将得到的拉普拉斯模板于原图像进行相加得到一幅经过锐化过的图像:
%%相加锐化后的结果
img2=photo+img1;
figure(3)
imshow(img2);
title('相加锐化后的结果')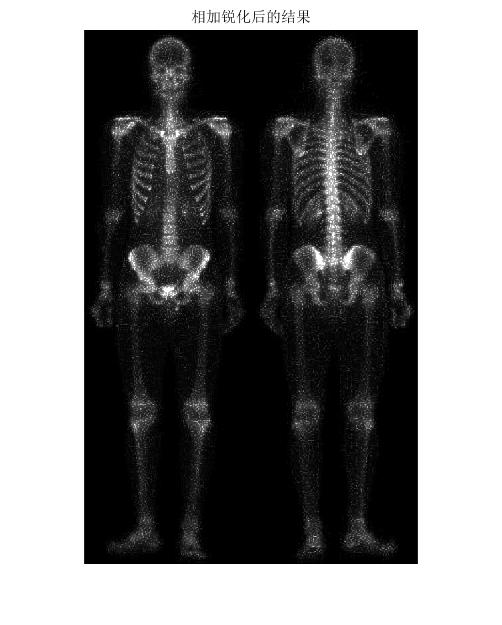
我们可以看到,相加后的图像含有相当多的噪声。我们很容易想到,降低噪声的一种方法是中值滤波器。然而中值滤波器是一种非线性滤波器,它有可能改变图像的性质,这在医学图像处理中是不能接受的。
另一种方法是使用原图像梯度操作的平滑形式所形成的一个模板。梯度变换在灰度变化的区域(灰度斜坡或台阶)的平均响应要比拉普拉斯操作的平均响应更强烈,而对噪声和小细节的响应比拉普拉斯操作的响应弱,而且可以通过均值滤波器对其进行平滑处理而进一步降低噪声。
这时,思路是对梯度图像进行平滑处理并用拉普拉斯图像于它相乘。这样,乘积会保留灰度变化强烈区域的细节,同时降低灰度变化相对平坦区域的噪声。这种处理可以粗略地看成是将拉普拉斯操作与梯度操作的优点相结合。将结果加到原图像上,就可以得到最终的锐化图像。
首先我们对原图像进行sobel梯度处理:
%%sobel梯度处理
w2=[-1,-2,-1,0,0,0,1,2,1];
w3=[-1,0,1;-2,0,2;-1,0,1];
img3=imfilter(photo,w2,'conv','replicate','same');
img4=imfilter(photo,w3,'conv','replicate','same');
img5=im2uint8(mat2gray(img3+img4));
figure(4)
imshow(img5);
title('Sobel梯度')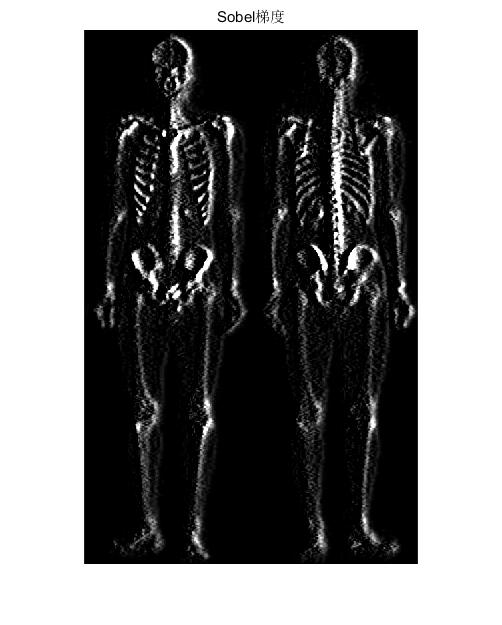
然后对其进行均值滤波:
%%均值滤波
m=5;
n=5;
w4=ones(m,n)/(m*n);
img6=imfilter(img5,w4,'conv','replicate','same');
figure(5)
imshow(img6);
title('均值滤波')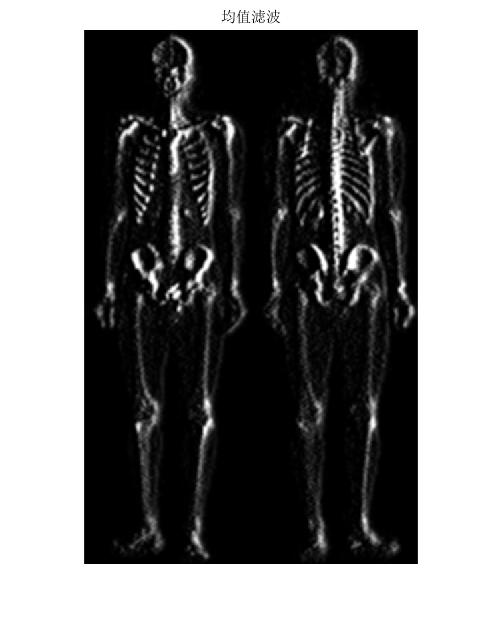
接下来将平滑后的拉普拉斯模板与Sobel模板相乘,注意强边缘的优势和可见噪声的相对减少。
%%相乘
img7=im2uint8(mat2gray(double(img1).*double(img6)));
figure(6)
imshow(img7);
title('平滑后的拉普拉斯模板与Sobel模板相乘')
然后将得到的模板与原图像相加处理得到锐化后的图像,与原图像相比,该图像中大部分细节的清晰度的增加都很明显,包括肋骨、颈椎骨、盆骨及颅骨。
%%相加
img8=im2uint8(mat2gray(photo+img7));
figure(7)
imshow(img8);
title('相加')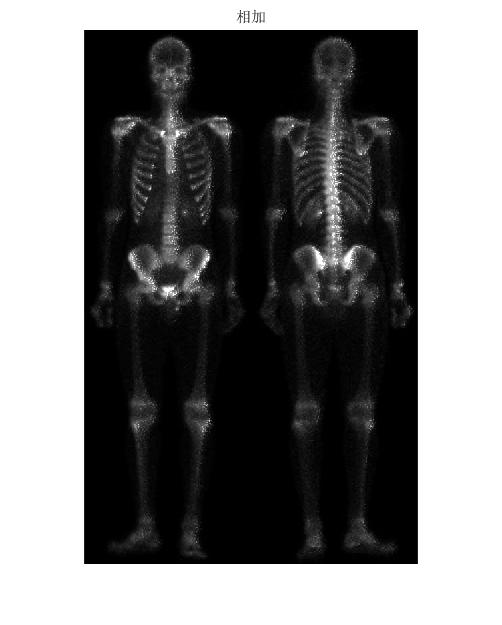
最后,我们增大锐化后图像的动态范围。根据前面几节介绍的方法,我们常用的有直方图均衡以及灰度变换的方法。这里对于图像的暗特性,我们采用幂律变换处理更好。由于我们希望能够扩展暗区域的灰度范围,因此γ必须小于1,这里我们设置γ=0.5,c=1.
%%幂律变换
c=1;
gama=0.5;
img9=im2uint8(mat2gray(c*double(img8).^gama));
figure(8)
imshow(img9);
title('幂律变换')
我们可以看出,经幂律变换后的图像与原图相比,出现了许多重要的新细节。围绕着手腕、手掌、脚踝和脚掌区域都是这种效果的很好例子。人体的整个骨架结构也很显著。包括手臂骨和腿骨。我们还注意到,人体轮廓及人体组织的清晰度不高。这是由于通过扩大灰度动态范围显示细节的同时也增大了噪声,但与原图相比还是显示出视觉效果的显著改进。
这篇关于冈萨雷斯数字图像处理-数字图像基础(Matlab)-图像的空间滤波的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!