『金融数据结构』「2. 从 Tick 到 Bar」

本文长度为 12825  字， 112  图表截屏 建议阅读 66 分钟
【在公众号对话框，回复  AFML2  可下载数据】

0引言

本文是 AFML 系列的第二篇

1. 金融数据类型

2. 从 Tick 到 Bar

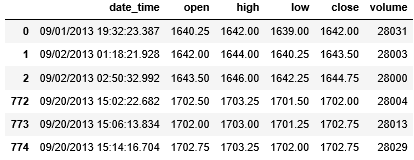
在做量化时，经常会用到下面格式的金融数据。

这条数据 (后文称作 bar) 包含 6 个属性：

1. 日期时间 (date_time) 是 2013 年 9 月 1 日 19 时 32 分 23 秒 387 毫秒
   

2. 起始价 (open) 是 1640.25

3. 最高价 (high) 是 1642.00

4. 最低价 (close) 是 1639.00

5. 结束价 (high) 是 1642.00

6. 成交量 (volume) 为 28031

注意我并有把 open 和 close 翻译成开盘价和收盘价，因为这条数据并不是按日来收集的，而它对应的时间精确到 387 毫秒。

另外为什么在一个时点上有四种不同的价格，即市场常见的 OHLC？ (每个字母代表 open, high, low, close 四个单词的首个字母)。原因是 OHLC 数据是在一段时间内 (上面 09/01/2013 19:32:23.387 是这段时间的终点) 收集很多 tick 数据的价格而决定的它们的 open, high, low, close，这段时间可以是

• 一天

• 一小时

• 一分钟

• 一秒

• 包含 1000 笔交易的那段时间

• 包含成交 100 个合约的那段时间

• 包含成交 10000 美元的那段时间

收集 tick 数据而生成某些统计量的操作叫抽样 (sample)，这些统计量可以是这些 tick 数据的

• 起始值、最大值、最小值、终止值 (OHLC)

• 简单平均值 (下面要介绍的 TWAP)

• 成交量加权平均值 (下面要介绍的 VWAP)

其实本帖讲的内容就是简单的抽样，从大量「tick 级别」的高频数据，选出有代表性「bar 类型」的样本。

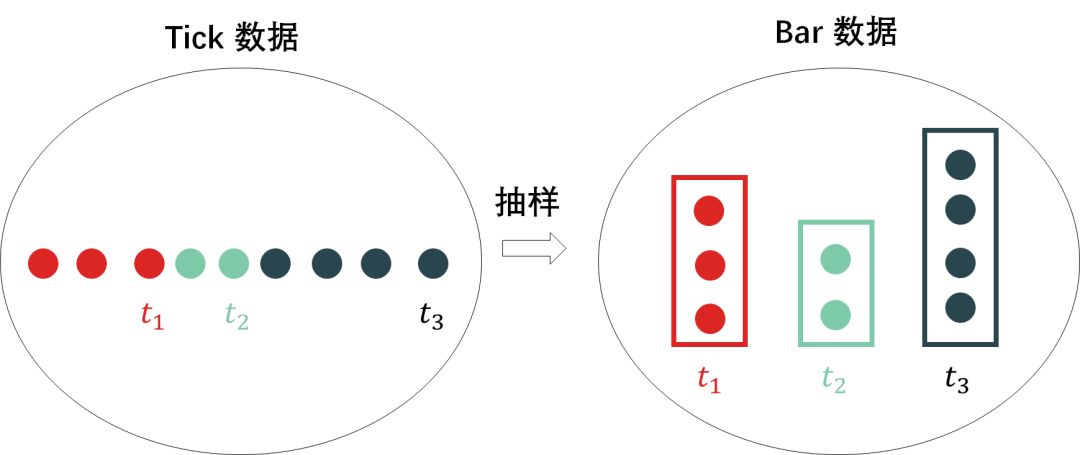
但本帖的内容很重要，很多人都迷恋复杂的算法，但往往忽略了数据的质量，有些时候并不是好的算法赢，而是好的数据赢。

本帖的目录如下：

目录

第一章 - Tick 和 Bar

    1.1 Tick 数据

    1.2 Bar 数据

第二章 - 标准 Bar

    2.1 比特币永续掉期高频数据

    2.2 等时抽样之 Time Bar

    2.3 等笔抽样之 Tick Bar

    2.4 等量抽样之 Volume Bar

    2.5 等额抽样之 Dollar Bar

第三章 - 信息驱动 Bar

    3.1 S&P 500 期货高频数据

    3.2 Imbalance Bar

    3.3 Runs Bar

总结

1Tick 和 Bar

1.1

Tick 数据

Tick 不是下左图中的水滴答的声音，而是下右图中某种金融产品交易时的逐笔数据。

Tick 数据也是交易所对定单薄 (order book) 中进行增加、删除、更新和成交四个操作产生的数据。换句话说，只要在定单薄中买价、买量、卖价和卖量发生变化，那么就产生一个 tick。下图展示了某加密货币的 tick 数据。

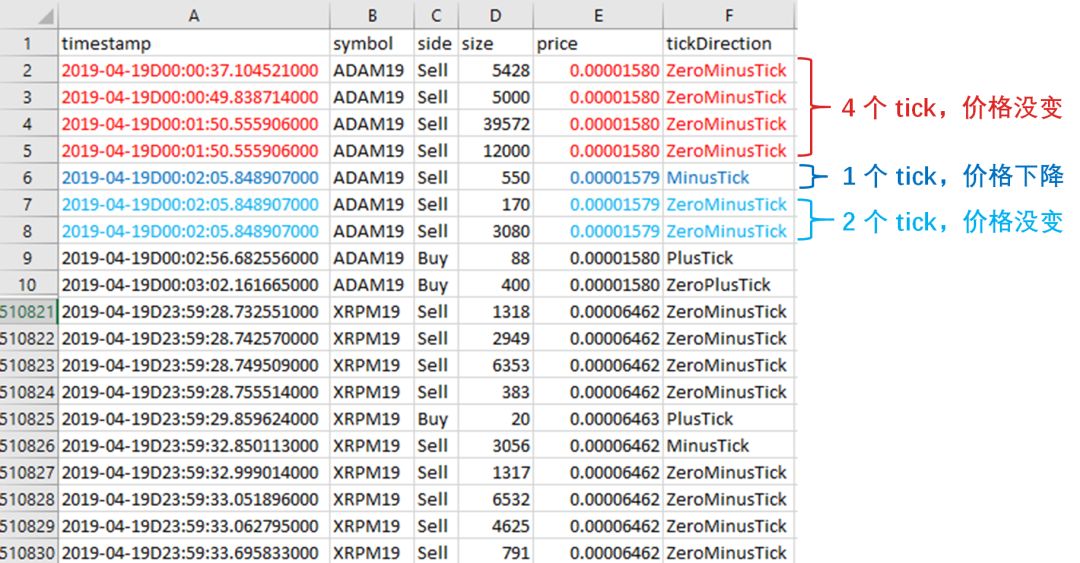
国内交易所发送是切片信息，还不是真正意义的 tick 信息。以切片间隔时间为 500 毫秒举例，一个切片相当于一份快照，然而这 500 毫秒内的任何变化，你是没法看到的。下图的立方体可想象成 tick 信息，红色立方体是快照每 500 毫秒捕捉到的，而深青色立方体是遗漏掉的。

以切片间隔时间为 500 毫秒，含三档行情 (三买单三卖单) 的定单薄来举例。

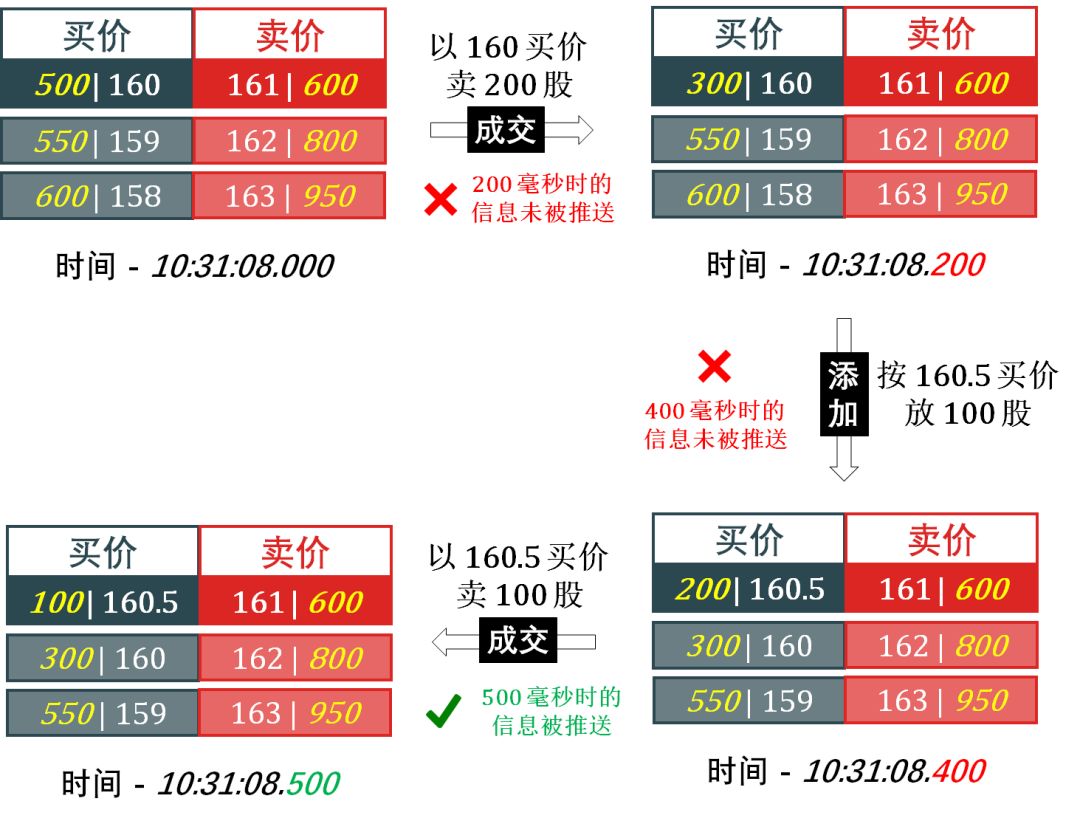
解释一下：

• 在 10 时 31 分 08 秒 200 毫秒的时候，有人以 160 的买价卖出 200 股，最新成交价为 160，总成交量为 200 股，但此时因为未到切片时间 (500 毫秒)，所以不会推送数据出来。

  
  

• 在 10 时 31 分 08 秒 400 毫秒的时候，有人想以 160.5 的价格卖 200 股，信息添加到限价定单薄上，此时仍未到切片时间，仍不会推送数据。

• 在 10 时 31 分 08 秒 500 毫秒的时候，有人以 160.5 的买价卖出 100 股，最新成交价为 160.5，总成交量为 300 股，此时交易所生成一份快照，并推送出来，这就是我们能够接收到的所谓的 tick 数据。实际上我们丢失了不少信息，不如我们根本不知道在 160 的时候也有成交。

按上图流程所示，如果 160 是当日的最低价，则可能会出现因为信息丢失而无法获得，所以国内交易所都会单独推送一份当日最高最低价以弥补。

1.2

Bar 数据

为了高频的 tick 数据从中提取有价值的信息，并以合适的形式存储它们。这种数据储存形式叫做 bar。这里的 bar 指的不是下左图中的酒吧，而是下右图里的一个单元。

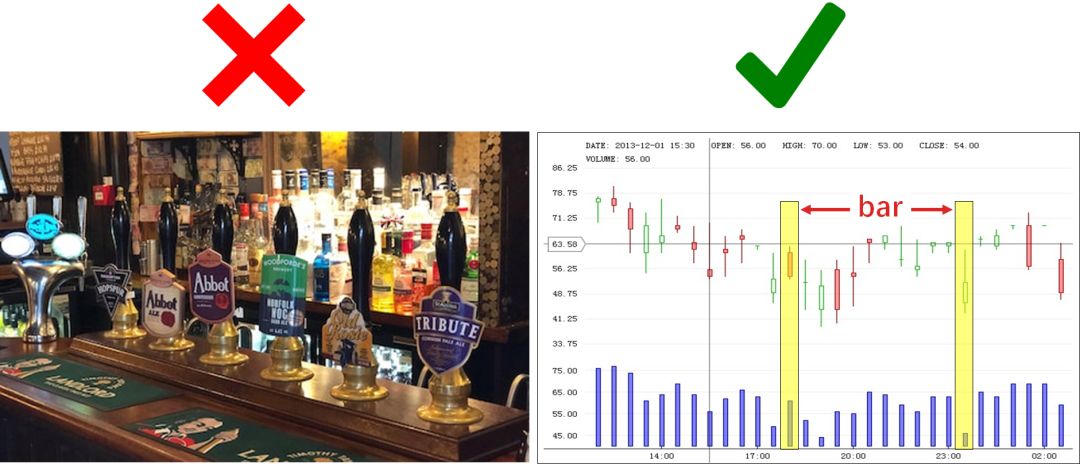
将右图的单元放大得到两种类型的 bar (绿色空心代表价格上升的 bar，红色实心代表价格下降的 bar)：

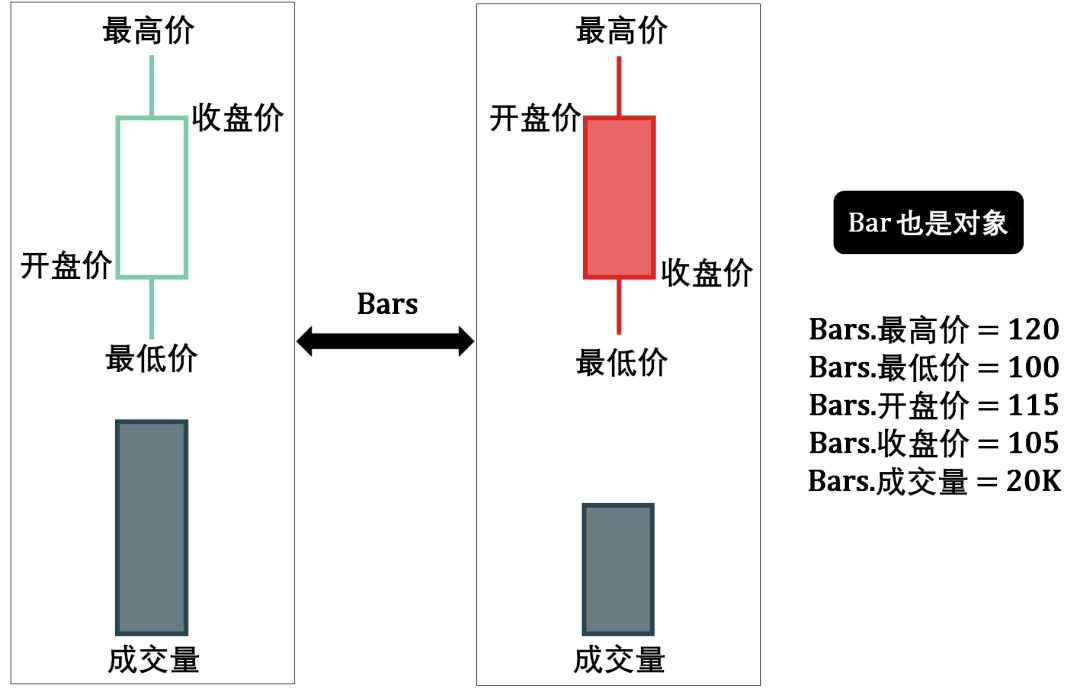
我在〖Python 系列〗里最喜欢说的一句就是「万物皆对象」，这里 bar 也不例外，也是个对象，它里面的属性有最高价 (high)、最低价 (low)、开盘价 (open)、收盘价 (close) 和成交量 (volume)。之后我们遇到的 bar 会有更多属性，比如时间戳 (timestamp)、代号 (symbol)、ID 等等。

搞量化时总不能把上面的 bar 图形当成数据格式储存吧，想想 DataFrame，把 bar 里每一条属性当成 Column，那么每一条记录 (observation) 或一个样例 (instance) 就是一个 bar，而 DataFrame 就是存储多个 bar 的数据结构 (再回到开头的那幅图)。

在后面两章，我们介绍如何构建

1. 文献中常见的标准 bar

2. 实践中复杂的信息驱动 bar

2标准 Bar

构建标准 bar 通过标准抽样 (regular sampling)，将非均匀序列的「原始数据」转化为均匀序列的「加工数据」。

2.1

比特币永续掉期高频数据

采用的是 BitMEX 交易所里交易的比特币/美元永续掉期 (XBTUSD perpetual swap)。XBTUSD 永续掉期合约则没有到期日，可以一直持仓。

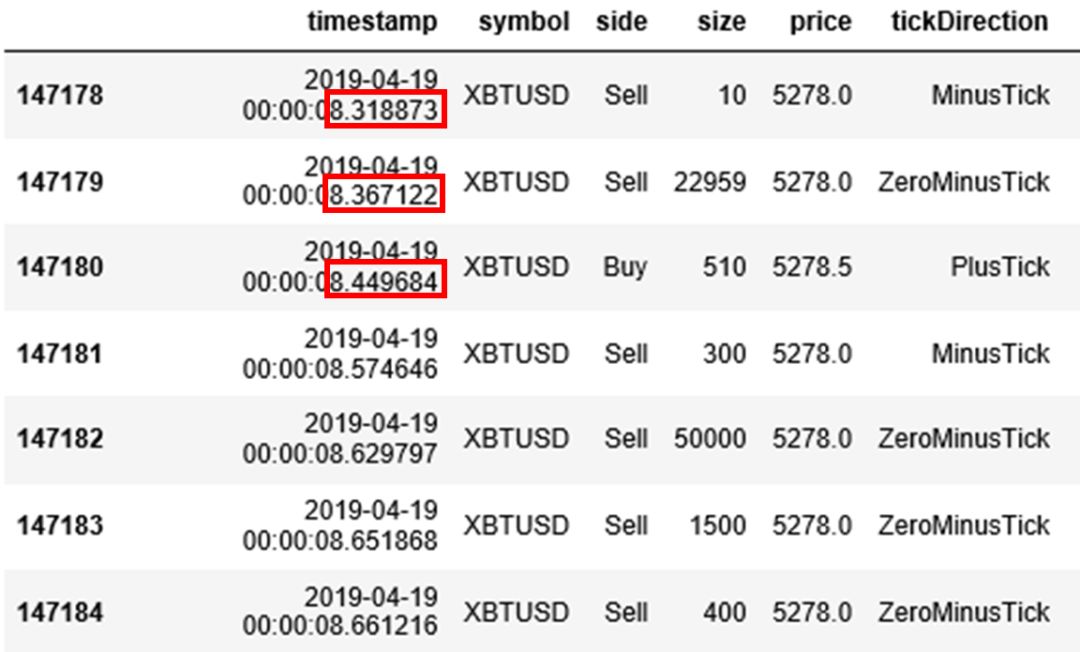
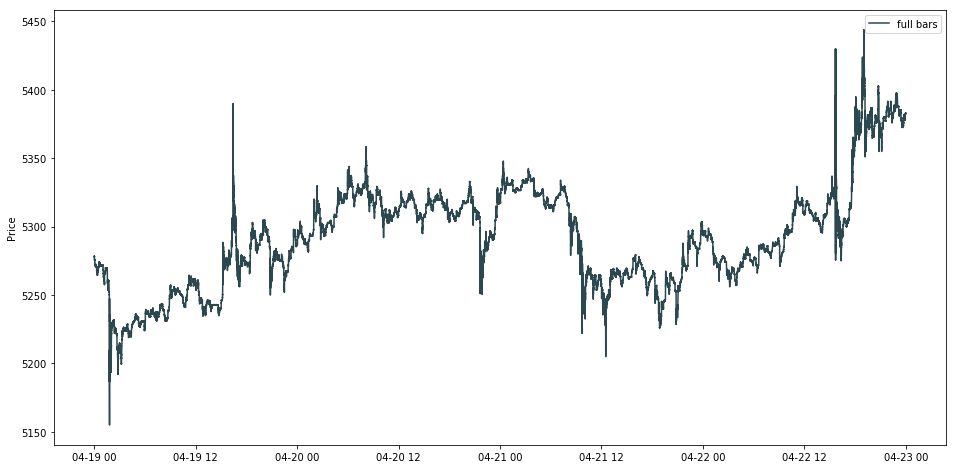
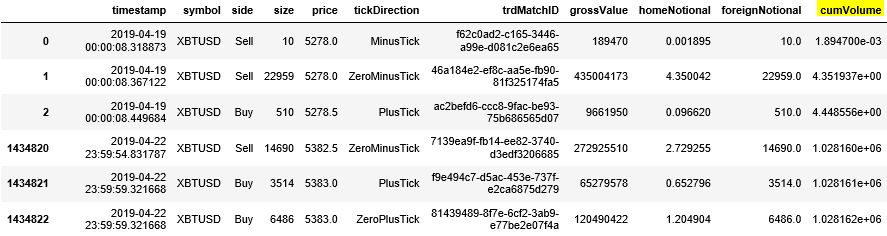
以 2019 年 4 月 19 日这一天 XBTUSD 永续掉期的交易数据为例，其原始数据记录每个有交易的时点下的信息。注意每个 tick 的时间戳 (time stamp) 的时间值是非均匀的，看下图红色框里的精确到秒后 6 位数字的三个时间，分别是 8.318873, 8.367122 和 8.449684。

接下来「读取-概览-处理-可视化」数据。

读取四天的高频数据，获取 symbol 为XBTUSD 的相关数据。发现有 1434823 条tick 数据，每条数据有 10 个特征。

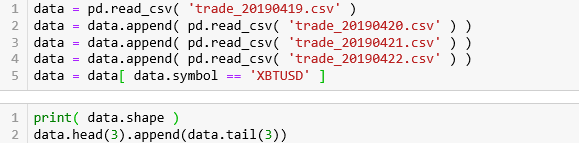
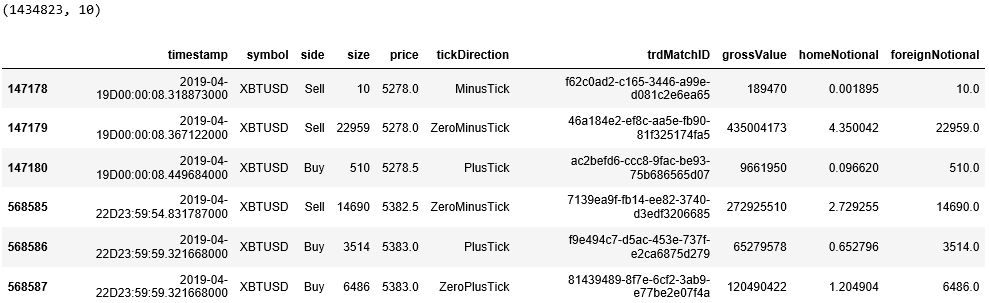
重要的五栏是

• side：买卖方向

• price：价格

• tickDirection：每笔的价格走向。

  • minusTick 是价格向下

  • zeroMinusTick 都是价格不变但前一个 tick 价格向下

  • plusTick 是价格向上

  • zeroPlusTick 都是价格不变但前一个 tick 价格向上

• homeNotional：合约数，即 volume

• foerignNotional：成交额，以美元为单位
  
  

---

由于 DataFrame 的行标签是 XBTUSD 并不是从 0 开始的 (从 csv 读取的原数据中含有好几种加密货币的永续掉期)，因此我们用 reset_index() 来重新给出行标签。

---

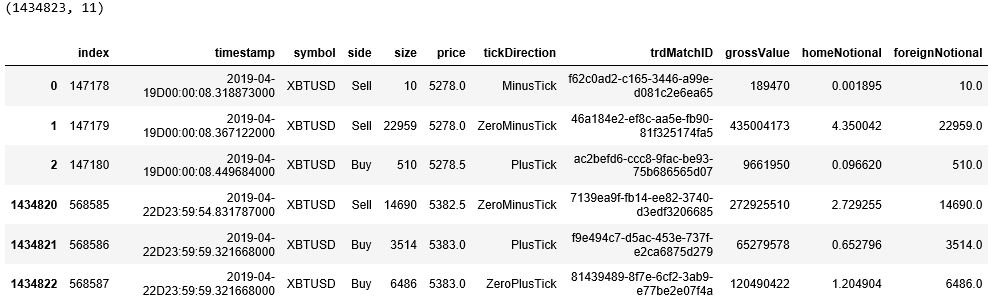
原来的行标签变成了列标签 index，其实上次信息没什么用，用 drop() 函数删除该列。

---

最后发现时间戳太长了，后面多了 3 个零根本用不到，而且中间还多了一个 ‘D’ 字符串，用 map() 函数将其转换成「年-月-日 时:分:秒.毫秒」标准格式。 

---

画出所有 tick 数据的线状图，发现有两个点呈现了「暴涨暴跌」。

在量化中，我们很多时候并不需要每条 tick 的高频信息，我们需要的是从中进行有效的抽样，比如下面介绍的等时抽样。

知识点 - 抽样

抽样是指从目标总体 (population) 中抽取一部分个体作为样本 (sample)，也可以对抽取出来的部分个体进行一些操作 (比如取平均) 作为一个样本。

抽样的目的是通过观察样本的属性，依据所获得的数据对总体的数量特征得出具有可靠性的估计判断，从而达到对总体的认识。

下面四节分别介绍等时抽样、等笔抽样、等量抽样和等额抽样。

在介绍过程中，我们也会用 Python 代码来实现它们。需要引入 numpy, pandas 和 matplotlib 必要的包，并定义我最喜欢的一些颜色 (看过我盘一盘 Python 系列的读者应该知道我的喜好 )。

import numpy as npimport pandas as pdimport matplotlib.pyplot as plt%matplotlib inline

dt_hex = '#2B4750'    # darkteal,  RGB = 43,71,80r_hex = '#DC2624'     # red,       RGB = 220,38,36g_hex = '#649E7D'     # green,     RGB = 100,158,125tl_hex = '#45A0A2'    # teal,      RGB = 69,160,162tn_hex = '#C89F91'    # tan,       RGB = 200,159,145

2.2

等时抽样

等时抽样是将 tick 数据转换为 time bars，在「固定段时间」中抽样得到 (比如固定每1, 15, 30, 60 分钟进行一次抽样)。

有了每个 time bar 里的一组 tick 数据，我们

• 可以找出 OHLC 四类价格 (K 线图)

• 也可以计算 (加权) 平均价格 (线状图)

我们先看看如果计算平均价格的。

在一段固定的时间 [T_s, T_e]，计算

• 时间加权平均价 (Time-weighted Average Price, TWAP)

• 成交量加权平均价 (Volume-weighted Average Price, VWAP)

来当做在 [T_s, T_e] 中的一个样本。

知识点 - TWAP, VWAP

假设在 [T_s,T_e] 中有 n 个数据，其中 T_s ≤ t₁ < t₂ < ⋯ < t_n ≤ T_e

TWAP 实际上是 n 个价格的简单算术平均

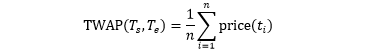
VWAP 是 n 个价格的成交量加权平均

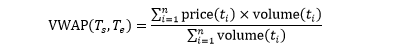
如果所有成交量相同，VWAP 和 TWAP 等价。业界普遍用 VWAP。

下面 Python 代码用来生成 VWAP：

def get_vwap( df ):    v = df['homeNotional']    p = df['price']    df['vwap'] = np.sum(p*v) / np.sum(v)    return df

在 XBTUSD 数据中，成交量在  'homeNotional'  栏下，价格在  'price'  栏下，套用下面公式计算出 VWAP 并添加到 df[ 'vwap' ] 栏下。

Time bars 的简单示意图如下：

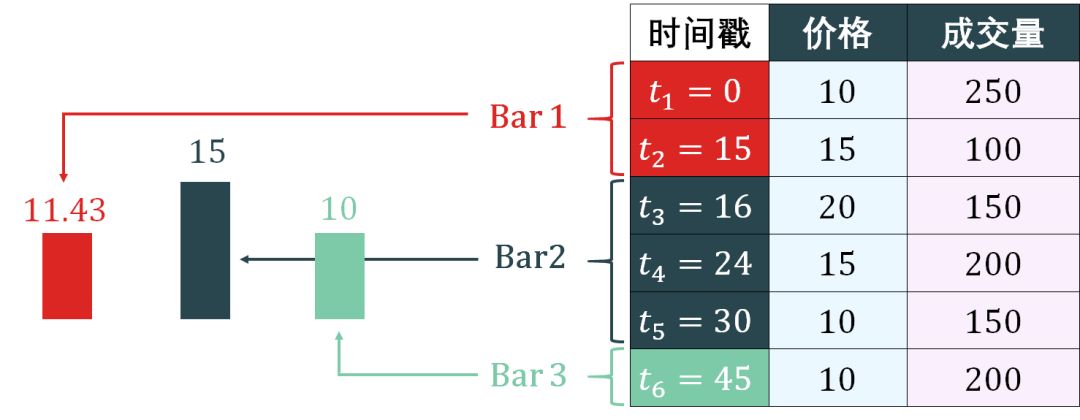
上图 time bars 根据每 15 分钟抽样得到 3 个 bar，分别计算出 VWAP。

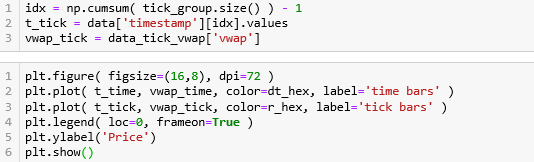
生成 time bars 的代码如下：

设置分组间隔为 15 分钟

1. 用 set_index() 函数将‘timestamp’作为 index。

2. 用 groupby() 函数将周期为15min的 Grouper 分组。

注意，pandas 里面的骚函数 Grouper 里的 freq 也可以方便的改成其他周期参数。

---

按照 15min 在原数据上分组，那么每个组的大小之和应该和原数据的大小一样，果然是 1434823 条数据。接着对每个组套用 get_vwap() 来计算 VWAP。

---

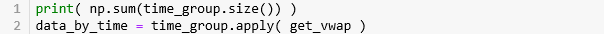
1434823

---

让我们看看按「等时抽样」下的每个 time bar 里含有多少个 tick 数据。

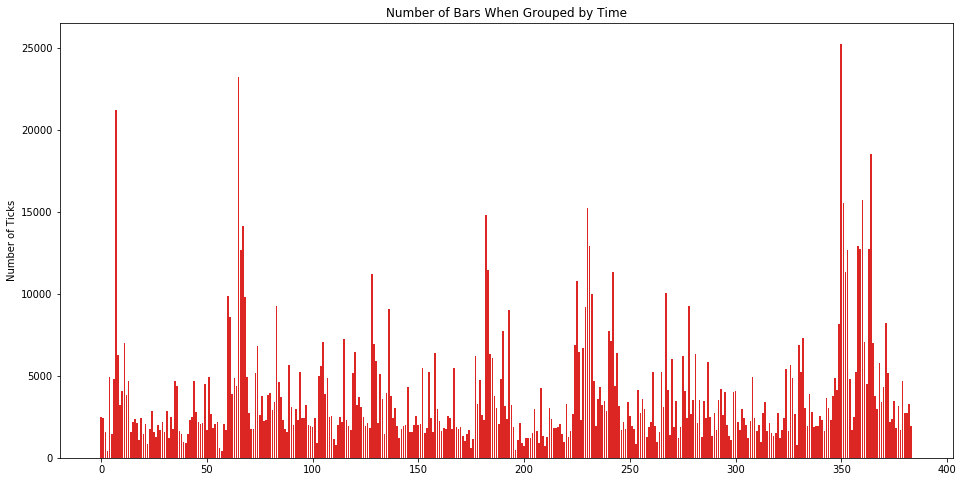
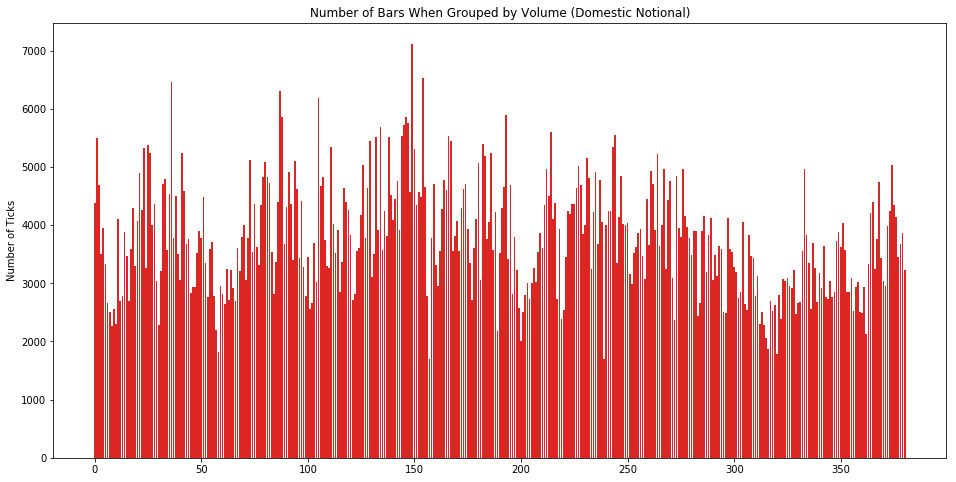
从图上可看出，不同时间段的交易活跃度差别很大，看到那几根很高的线了么？

---

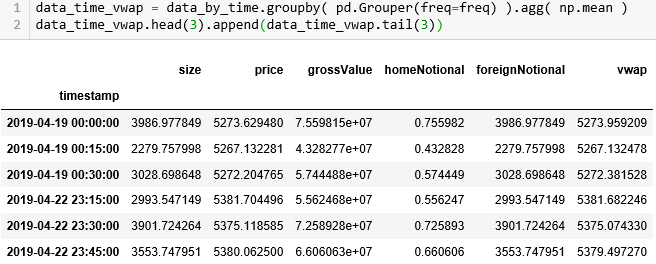
由于我们定义的  get_vwap() 函数是在每一行上计算一个 VWAP，假设一组有 100 行，那么这 100 行都含有一样的 VWAP 值，我们用 np.mean 来整合 VWAP 存到 data_time_vwap。注意它的 timestamp 都是以 15 分钟为间隔的。

---

画出 time bar 的线状图。

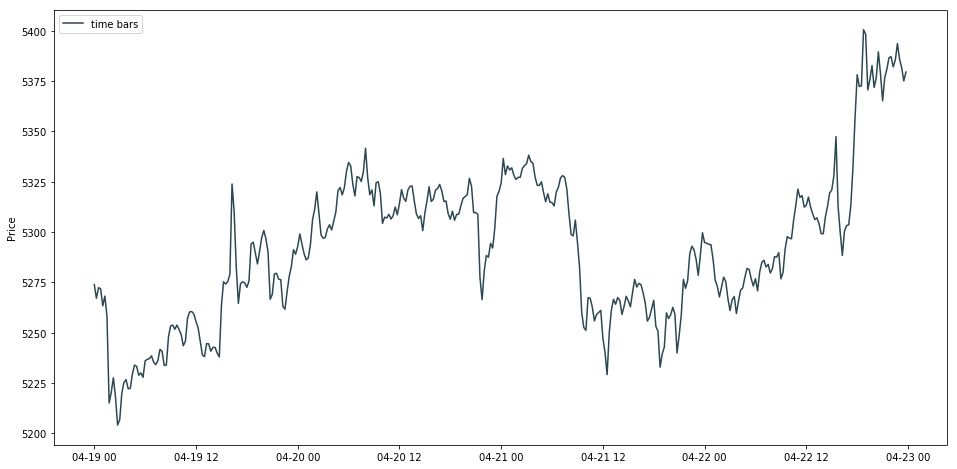
Time bars 是最普遍的，但是它有两个缺点：

1. 信息从来都不会均速在市场流动，比如股市开盘交易比临近中午交易要活跃的多。

   
   

2. 等时抽样得到的序列通常呈现自相关 (serial correlation)，异方差 (heteroscedasticity) 和收益非正态 (non-normal return) 等不好的性质。

怎么改进？用「等笔抽样」方法。

2.3

等笔抽样

等笔抽样是将 tick 数据转换为 tick bars，以每段时间含「固定笔数」的前提下中抽样得到 (比如固定每 1000, 2000, 3000 笔进行一次抽样)。

这个固定的笔数如何确定呢？通常来说我们对每长时间抽样一次有个概念(如每 15 分钟)，然后得到 bar 的个数 (3 个)。同样，在等笔抽样下，我们也希望大概得到 3 个bar (即每个 bar 里含 2 个 tick)。

 

    每个 bar 含 tick 数 = tick 总数 / bar 数

Tick bars 的简单示意图如下：

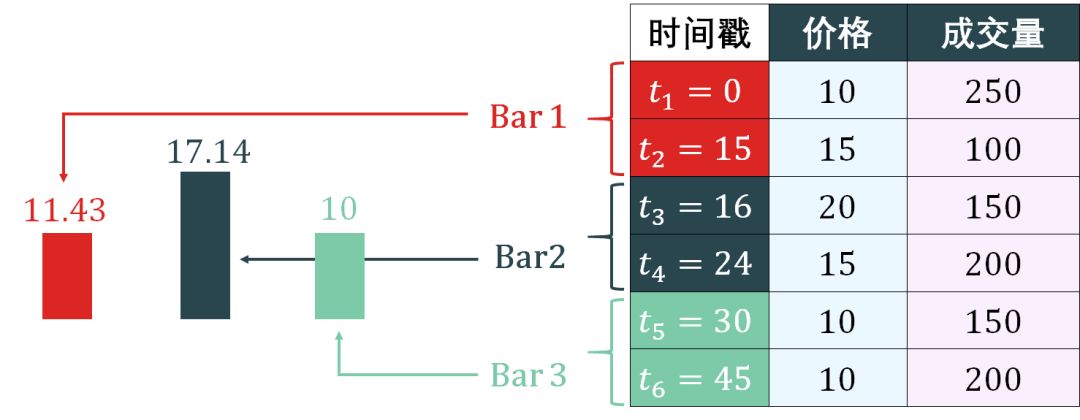
 生成 tick bars 的代码如下：

第 1 行计算 bar 的数量 384，第 2 行计算 tick 的总数量 1434823，第 3-4 行计算每条 bar 中 tick 的数量并弄成整百 3700 (例如：3714 就转化成 3700)。

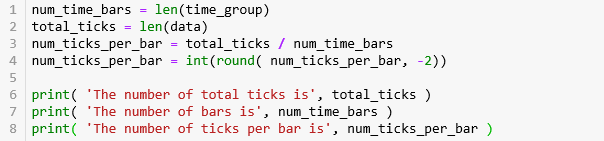
The number of total ticks is 1434823
The number of bars is 384
The number of ticks per bar is 3700

---

第 2-3 行用运算符 // 对 df.index 进行取整，[0, 1, 2, 3, 4, 5] // 3 就等于 [0, 0, 0, 1, 1, 1]。取整的数被巧妙的当成 groupID 用来分组。

从结果来看 (注意黄色高亮处)，在 GroupID 0 下，tick 的 ID 从 0 到 3699，没错就是 3700 个。

---

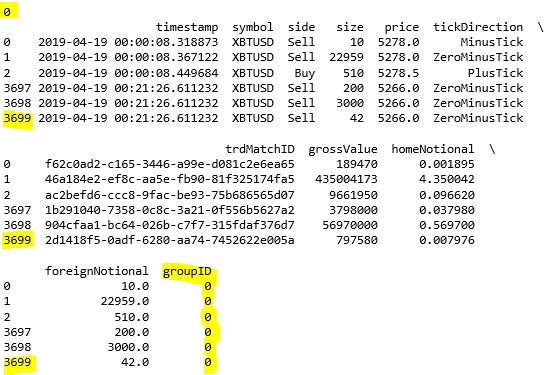
让我们看看按「等笔抽样」下每个 tick bar 里含有多少个 tick 数据，当然 3700 个啦，除了最后一个不是，因为不会那么巧 tick 总数能被 bar 数整除。

---

再确认一下 tick_group 里的总数据也是 1434823 条，接着对每个组套用 get_vwap() 来计算 VWAP。

1434823

---

由于我们定义的 get_vwap() 函数是在每一行上计算一个 VWAP，假设一组有 100 行，那么这 100 行都含有一样的 VWAP 值，我们用 np.mean 来整合 VWAP 存到 data_tick_vwap。

---

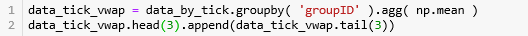
此时我们需要每个 tick bar 对应的时间戳。简单，用其组的大小累加作为索引就行了。获取时间戳后，画出 tick bar 的线状图。

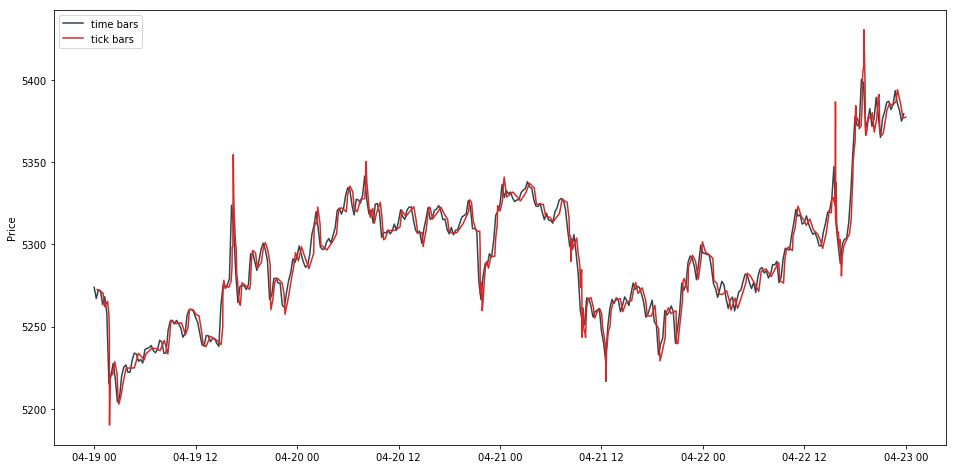
tick bar 和 time bar 的图基本一致，就是在几个暴涨和暴跌点更加极端。 

等笔抽样的优点：

一些研究发现按 tick bar 来取样得到的数据更接近独立正态同分布 (IID)，而 IID 在统计上的均值和方差都有非常好的性质。

等笔抽样的缺点：

不过 tick bar 也有自身的问题，假设你下单要买 1000 股阿里巴巴，一次性的话就记录成 1 个 tick，但是分 10 单每单 100 股来买的话，就记录成 10 个 tick。这样明显不太合理。

怎么改进？用「等量抽样」方法。

2.4

等量抽样

等量抽样是将 tick 数据转换为 volume bars，以每段时间含「固定成交量」的前提下中抽样得到 (比如固定每 1000 股阿里巴巴，每 200 手玉米期货进行一次抽样)。

这个固定的成交量如何确定呢？和等笔抽样中的方法一样，先得到 bar 的个数 (3 个)。在等量抽样下，我们计算累积成交量再除以 bar 的个数。

    每个 bar 含的成交量 = 总成交量 / bar 数

Volumn bars 的简单示意图如下：

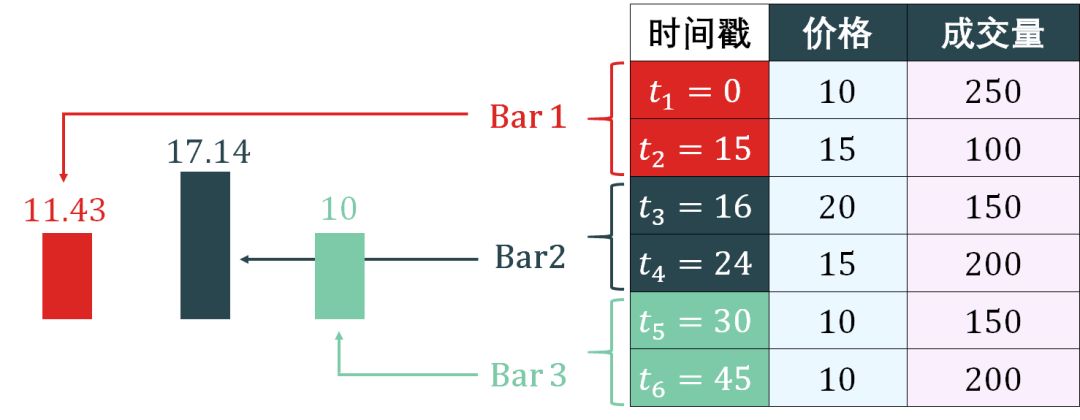
上图好像和 tick bars 的一样，但后面的逻辑不一样。抽样 volume bar 的方法是：

1. 计算总成交量是 1050

2. 计算每个 bar 的成交量是 350 = 1050/3 

3. 用 350 作为标准来组成 bar，很明显第 1-2 个 tick 组成 bar 1，第 3-4 个 tick 组成 bar 2，第 5-6 个 tick 组成 bar 3。

生成 volumn bars 的代码如下：

首先用 cumsum() 函数计算累积成交量 'homeNotional'，用 assign() 函数并储存在 DataFrame 的 'cumVolume' 栏下。

---

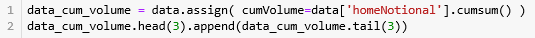
第 1 行计算 总成交量 1028161.8，第 2-3 行计算每条 bar 含的成交量并弄成整百 2700 (例如：2714 就转化成 2700)。

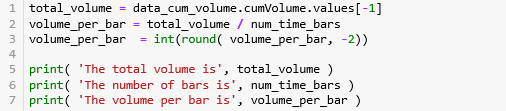
The total volume is 1028161.8162190766
The number of bars is 384
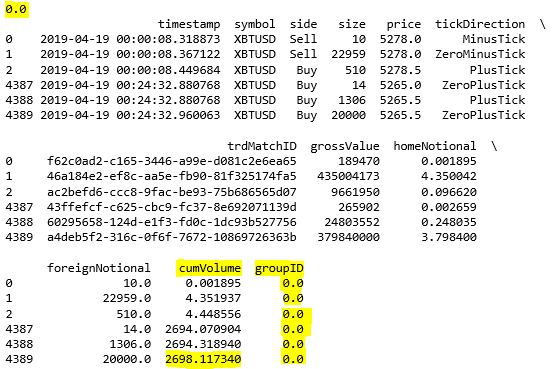
The volume per bar is 2700

---

第 2-3 行用运算符 // 对 df.cumVolume 进行取整，[0, 1000, 2000, 3000, 4000, 5000] // 2700 就等于 [0, 0, 0, 1, 1, 1]。取整的数被巧妙的当成 groupID 用来分组。

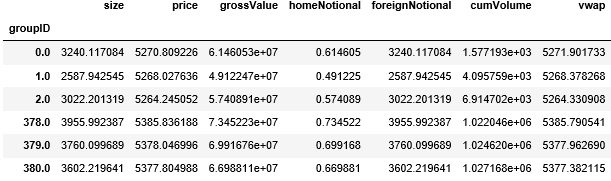
从结果来看 (注意黄色高亮处)，在 GroupID 0 下，cumVolume 最后的值是 2698.11，非常接近 2700。

---

让我们看看按「等量抽样」下每个 volume bar 里含有多少个 tick 数据。从下图看分布还算比较平均。

---

由于我们定义的 get_vwap() 函数是在每一行上计算一个 VWAP，假设一组有 100 行，那么这 100 行 都含有一样的 VWAP 值，我们用 np.mean 来整合 VWAP 存到 data_volume_vwap。

---

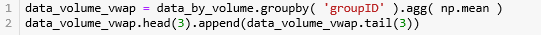
此时我们需要每个 volume bar 对应的时间戳。简单，用其组的大小累加作为索引就行了。获取时间戳后，画出 volume bar 的线状图。

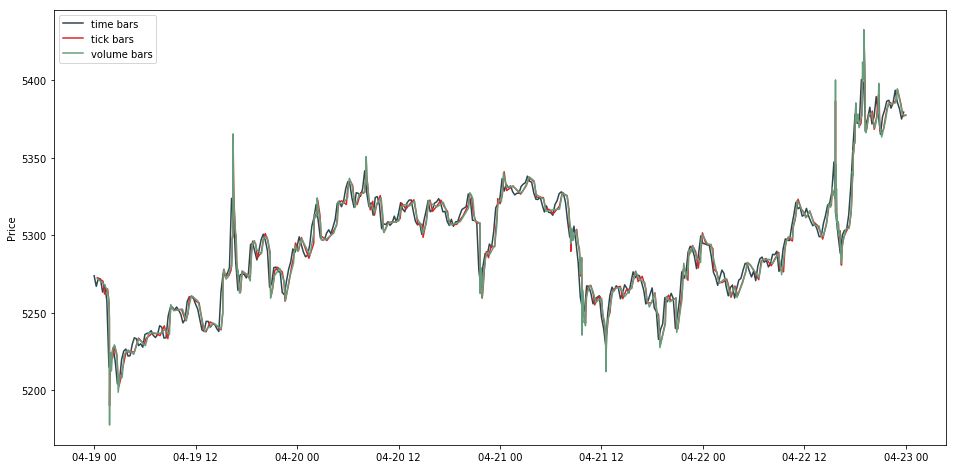
等量抽样优点：

一些研究发现按 volume bar 来取样得到的数据比 tick bar 更接近独立正态同分布 (IID)，此外不少关于市场微观理论都是基于价格和成交量来研究的，因此用 volume bar 能更好的结合那些研究。

等量抽样缺点：

不过 volume bar 也有自身的问题，假设迅雷股票在 6 个月内从 6 美元涨了 400% 到 24 美元，一开始你买了 1000 股迅雷花了 6000 美元，那么在终止点卖只需要卖 250 股票 (6000 美元) 就能回本。如果按 volume bar 来看，1000 股到 250 股波动很大，但实际上成交额都是 6000 美元。此外，股票的量在分割 (split) 和反向分割 (reverse split) 都会变化很大，但股票的额并没有变。

怎么改进？用「等额抽样」方法。

2.5

等额抽样

等额抽样是将 tick 数据转换为 dollar bars，以每段时间含「固定成交额」的前提下中抽样得到 (比如固定每 10000 美元)。这里的 dollar 泛指交易产品的计价货币 (denominated currency)，也可以是欧元、英镑、日元或人民币。

这个固定的成交量如何确定呢？和等量抽样中的方法一样，先得到 bar 的个数 (3 个)。在等额抽样下，我们计算累积成交额再除以 bar 的个数。

    每个 bar 含的成交额 = 总成交额 / bar 数

Dollar bars 的简单示意图如下：

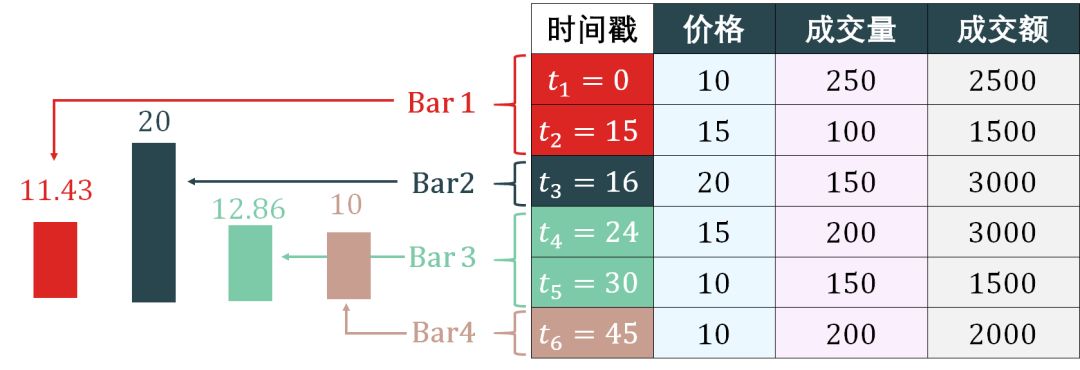
抽样 dollar bar 和抽样 volume bar 的方法是类似的：

1. 计算总成交额是 13500

2. 计算每个 bar 的成交额是 4500 = 13500/3 

3. 用 4500 作为标准来组成 bar，前 2 个 tick 接起来的成交额为 4000，但 3 个 tick 接起来的成交额为 7000 了，因此第 1-2 个 tick 组成 bar 1，第 3 个 tick 单独组成 bar 2，第 4-5 个 tick 组成 bar 3，第 6 个 tick 单独组成 bar 4。

生成 dollar bars 的代码如下：

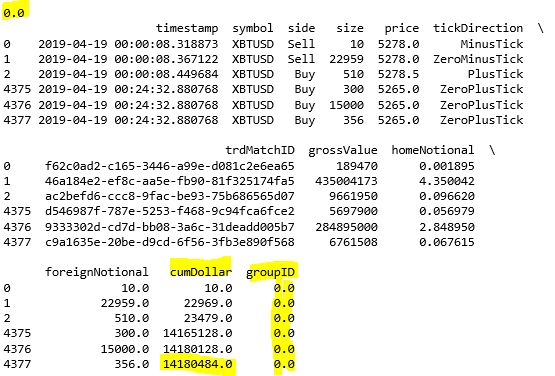
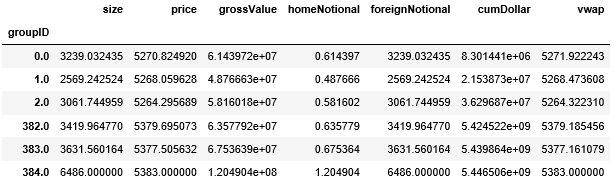
首先用 cumsum() 函数计算累积成交额 'foreignNotional'，用 assign() 函数并储存在 DataFrame 的 'cumDollar' 栏下。

---

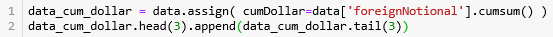
第 1 行计算 总成交额 5446505640，第 2-3 行计算每条 bar 含的成交额并弄成整百 14183600 (例如：14183614 就转化成 14183600)。

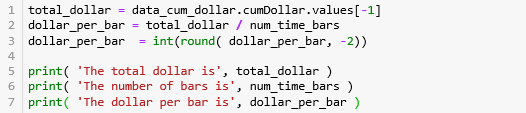
The total dollar is 5446505640.0
The number of bars is 384
The dollar per bar is 14183600

---

第 2-3 行用运算符 // 对 df.cumDollar 进行取整，[0, 1000, 2000, 3000, 4000, 5000] // 2700 就等于 [0, 0, 0, 1, 1, 1]。取整的数被巧妙的当成 groupID 用来分组。

从结果来看 (注意黄色高亮处)，在 GroupID 0 下，cumDollar 最后的值是 14180484，非常接近 14183600。

---

让我们看看按「等额抽样」下每个 dollar bar 里含有多少个 tick 数据。从下图看分布还算比较平均。

---

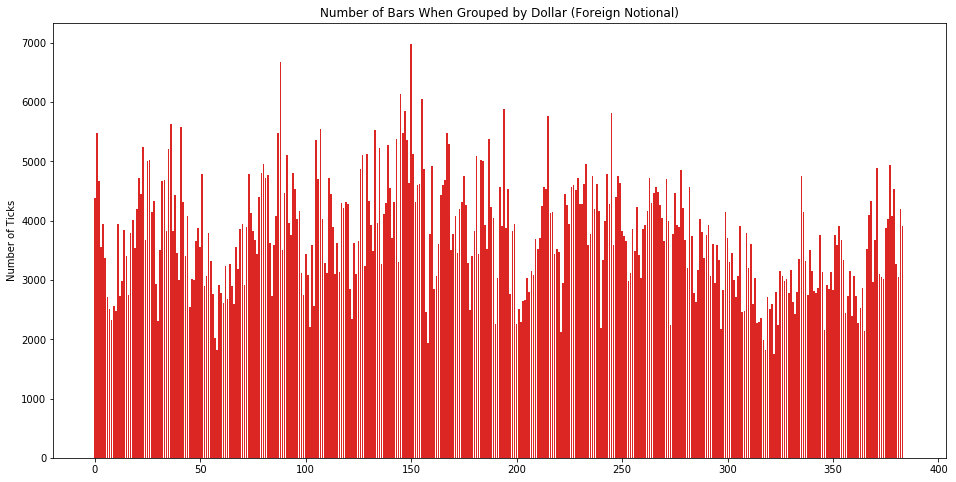
由于我们定义的 get_vwap() 函数是在每一行上计算一个 VWAP，假设一组有 100 行，那么这 100 行都含有一样的 VWAP 值，我们用 np.mean 来整合 VWAP 存到 data_dollar_vwap。

---

此时我们需要每个 dollar bar 对应的时间戳。简单，用其组的大小累加作为索引就行了。获取时间戳后，画出 dollar bar 的线状图。

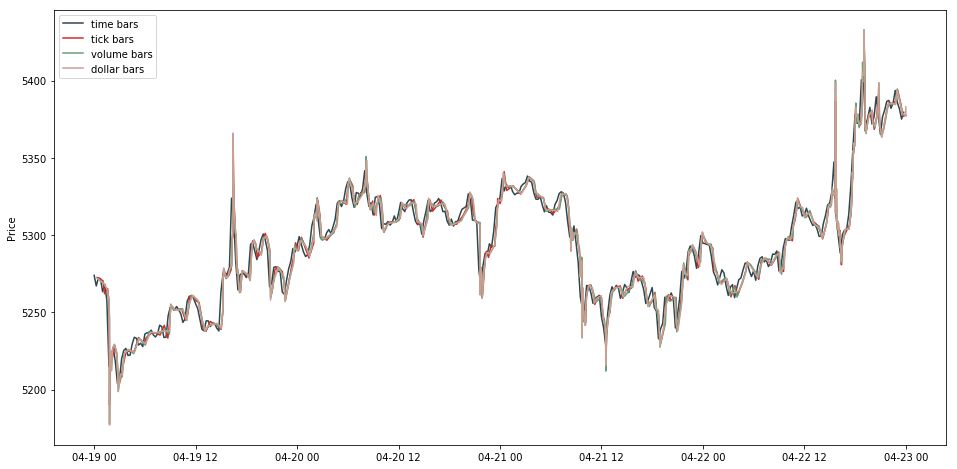
使用成交额相对而言是有一定优势的。假设一只股票在一定时间区间内股价翻倍，期初 10000 元可以购买的股票将会是期末 10000 元可购买股票手数的两倍。在股价有巨大波动的情况下，tick bars 和 volume bars  每天的数量都会随之有较大的波动。除此之外，增发、配股、回购等事件也会导致 tick bars 和 volume bars 每天数量的波动。一般来说，等额抽样相比较而言是一个更加稳健的抽样方法。

3信息驱动 Bar

构建信息驱动 bar 在更多信息进入市场时进行更频繁的抽样。当买卖不均衡时，市场参与者之间的信息差也变大，市场会出现知情交易者(informed trader)。在抽样时考虑买卖不均衡，我们可以在价格达到新的均衡水平之前做出决定。信息驱动 bar 也分两种：

1. Imbalance Bars (IB) 系列：TIB, VIB, DIB

2. Runs Bars (RB) 系列：TRB, VRB, DRB

上面缩写里的 T, V, D 代表的是 tick, volume, dollar。

3.1

S&P 500 期货高频数据

S&P 500 E-mini 期货 tick 级别的数据。该数据有人画 1000 美元从 Tick Data LLC 买来做研究的。数据每个属性的介绍如下。

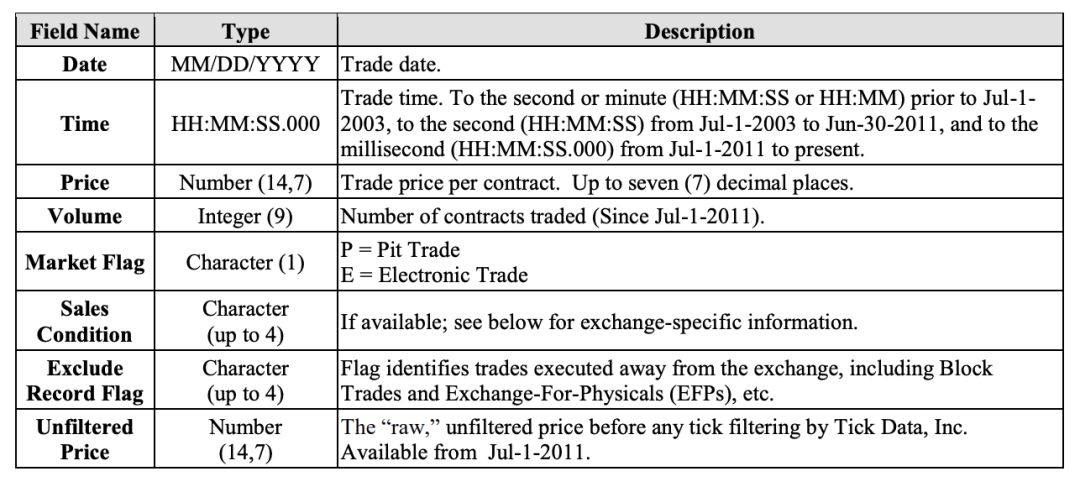
接下来「读取-概览-处理」数据。

从 csv 读数据并看首尾 3 行。

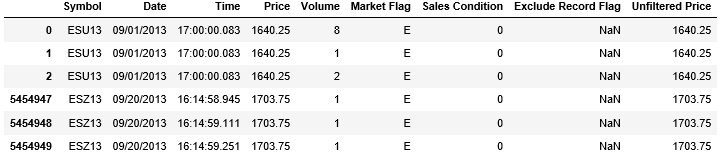
该数据包含 2013 年 9 月 1 日到 9 月 20 日的 5454949 条数据。数据太大我们只选取必要的特征 Date, Time, Price 和 Volume 来创建一个新的小一点的 DataFrame。

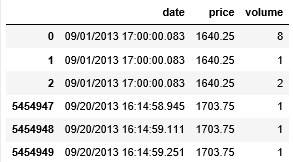
我们可以将 new_data 存成 csv 文件供以后重复使用。

new_data.to_csv('raw_tick_data.csv', index=False)

本章我们不自己编写代码，而是用更方便的 mlfinlab 的 API 来抽样信息驱动 bar。首先引入 mlfinlab 起别名为 ml。

import mlfinlab as ml

让我们先看看用 mlfinlab 里的函数来获取上节讲的 time bar, tick bar, volume bar 和 dollar bar。

从上面函数名字就能知道在做什么了：

• get_dollar_bars：获取 dollar bar

• get_volume_bars：获取 volume bar

• get_tick_bars：获取 tick bar

人家的 API 就是考虑周到，怕数据太大不是在 DataFrame 直接抽样，而是从 csv 数据中分不同批 (batch) 边读取边抽样。参数 threshold 决定每个 bar 大概应该包含的 tick 数、成交量和成交额是多少，而参数 verbose=True 是为了打印出程序运行信息。

---

看看这三个 bars 长什么样子。

tick.head(3).append(tick.tail(3))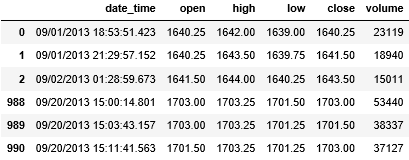

volume.head(3).append(volume.tail(3))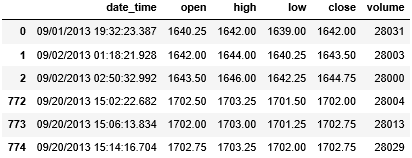

dollar['value'] = dollar['close'] * dollar['volume']dollar.head(3).append(dollar.tail(3))

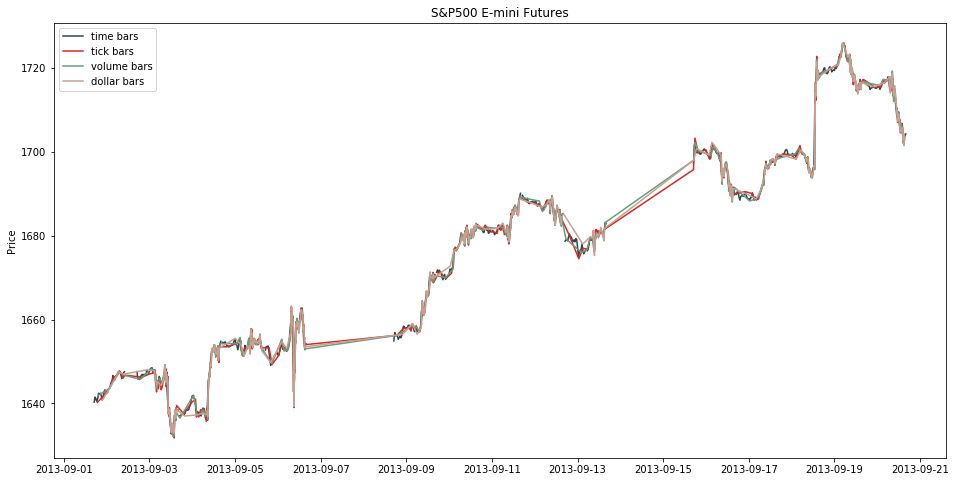
在 mifinlab 中没有抽样 time bar 的函数，因此我们用上节讲的，把 freq 设为 30min。画出四个 bars 的线状图。

好了热身结束，让我们来看看如果用 mlfinlab 来实现

1. Imbalance Bars (IB) 系列：TIB, VIB, DIB

2. Runs Bars (RB) 系列：TRB, VRB, DRB

3.2

Imbalance Bar

Tick Imbalance Bars

对每个时点 t (t = 1, 2, …, T)，我们有价格 p_t 和成交量 v_t 两个序列

• 价格序列 = {p₁, p₂, …, p_T}

• 成交量序列 = {v₁,v₂, …, v_T}

基于「价量」序列，我们定义一个「衡量买卖均衡度」的变量 b_t

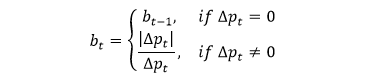
从 t-1 到 t 时，计算价格变化 △p_t = p_t - p_t-1

• 当价格不变时，即 △p_t = 0 时，均衡度不变，即 b_t = b_t-1

• 当价格变化时，即 △p_t ≠ 0 时，均衡度由的符号决定，即 b_t = |△p_t|/△p_t

容易看出 b_t 只能取值 ±1，而 b₀ 没有定义，取「前一个」bar 里的 b_T 值。

b_t 只是衡量在时点 t 的均衡度，那么累加所有 b_t 可得到「累积均衡度」，用 θ_T 来表示

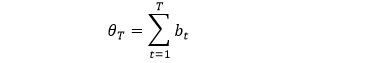
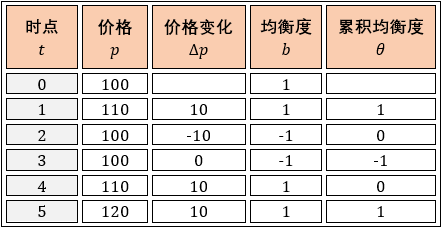
上面的符号有点抽象是么？我们在下表用一个具体例子来解释 p, b 和 θ 之间的关系 (假设 5 个时点，假设 b₀ = 1)，套用上面公式计算下就清楚了。

我们希望能够找到一个时点 T*，使得「累积均衡度」θ_T* 的绝对值超过一个阈值，这个阈值可以用 0 时点 θ_T 的期望来表示，即 E₀[θ_T]。用数学将前面的意思表达出来

在阈值的期望表达式 E₀[θ_T] 中，T 是随机变量，因为不知道什么时候 |θ_T| 超过阈值。专业上称 T 是停时 (stopping time)，b 是一个随机过程，而 b_T 就用来表示过程 b 在 T 时刻停止。接下来求这个阈值。

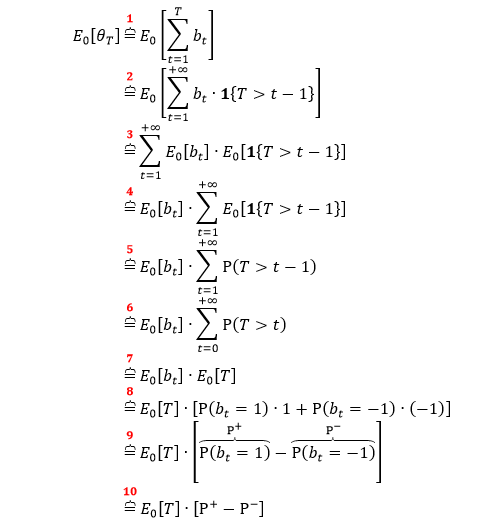
第 1 行套用 θ_T 定义。

第 2 行将索引 T 扩展到 +∞，并添加指标函数 1{T>t-1}。

第 3 行将期望符号和累加符号互换。

第 4 行提出公共因子 E₀[b_t]。

第 5 行用到 E[1(A)] = P(A) 性质。

第 6 行将索引从 1 移到 0。

第 7 行根据 E₀[T] 定义。 

第 8 行展开 E₀[b_t] 表达式。

第 9-10 行化简公式。

上式中

• E₀[T] 是每个 bar 含有 tick 数的期望

• P⁺ = P(b_t = 1) 是该 tick 被划分为「买」的无条件概率

• P^– = P(b_t = -1) 是该 tick 被划分为「卖」的无条件概率

 

买卖的无条件概率加起来为 1，即 P⁺+ P^– = 1，因此可将上式化简成

在实操中

• E₀[T] = 历史数据 T 的指数加权平均值 (exponentially-weighted moving average, EMA)

• P⁺ = 历史数据「买单占比」的 EMA

当算出阈值 E₀[θ_T] 之后，我们终于可以定义不等笔抽样 (tick imbalance bar, TIB)，类比一下等笔抽样 (tick bar),

• 不等笔抽样是按「不固定笔数」的前提下抽样得到。

• 等笔抽样是按「固定笔数」的前提下抽样得到。

 

TIB 抽样的集合为

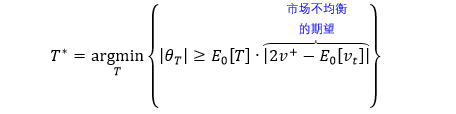
市场不均衡的预期用 U = |2P⁺ - 1| 来量化，U 越大市场越不均衡。

• 当买方压力很大，P⁺ ≈ 1, U ≈ 1，市场不均衡

• 当卖方压力很大，P⁺ ≈ 0, U ≈ 1，市场不均衡

• 当买卖压力相当，P⁺ ≈ 0.5, U ≈ 0，市场均衡

当 |θ_T| 比预期更加不均衡，T 越小这种情况越容易发生 (E₀[T] 越小)，这时抽样也就越频繁。

Volume Imbalance Bars

VIB 的推导逻辑和 TIB 类似，只不过把 b_t 换成 b_tv_t，公式推导如下：

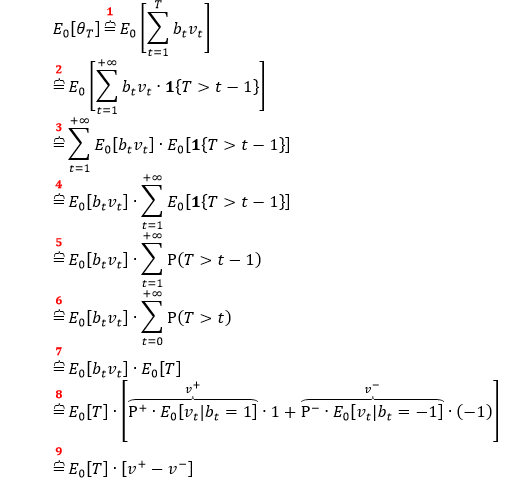
和 TIB 里面唯一的区别就在第 8 行。

上式中

• E₀[T] 是每个 volume bar 含有的期望笔数

• v⁺ 是成交量在「买」时的期望贡献

• v^– 是成交量在「卖」时的期望贡献

即 v⁺+ v^– = E₀[v_t]，因此可将上式化简成

在实操中

• E₀[T] = 历史数据 T 的EMA

• 2v⁺ - E₀[v_t] = 历史数据 b_tv_t 的 EMA

当算出阈值 E₀[θ_T]之后，我们终于可以定义不等量抽样 (volume imbalance bar, VIB)，类比一下等量抽样 (volume bar),

• 不等量抽样是在「不固定成交量」的前提下抽样得到。

• 等量抽样是在「固定成交量」的前提下抽样得到。

 

VIB 抽样的集合为

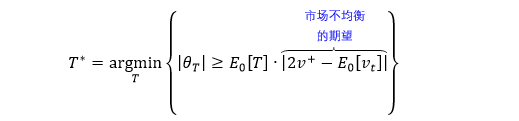
同理，市场不均衡的预期用 U = |2v⁺ - E₀[v_t]| 来量化，U 越大市场越不均衡。当 |θ_T| 比预期更加不均衡，T 越小这种情况越容易发生 (E₀[T] 越小)，这时抽样也就越频繁。

Dollar Imbalance Bars

DIB 的推导逻辑和 VIB 更是一模一样，只不过把 b_tv_t 换成 b_tq_t，公式推导如下：

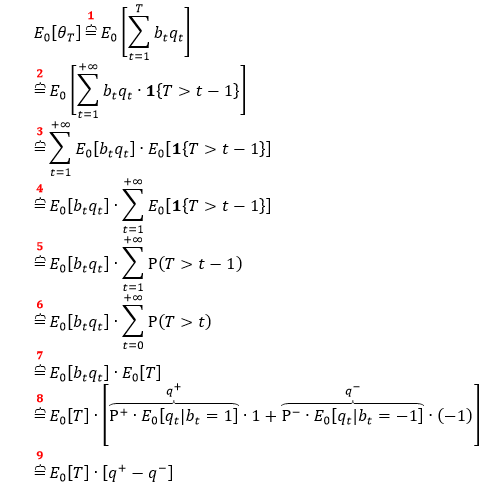
上式中

• E₀[T] 是每个 dollar bar 含有的期望笔数

• q⁺ 是成交额在「买」时的期望贡献

• q^– 是成交额在「卖」时的期望贡献

即 q⁺+ q^– = E₀[q_t]，因此可将上式化简成

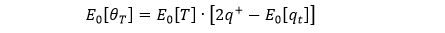
在实操中

• E₀[T] = 历史数据 T 的EMA

• 2q⁺ - E₀[q_t] = 历史数据 b_tq_t 的 EMA

当算出阈值 E₀[θ_T]之后，我们终于可以定义不等额抽样 (dollar imbalance bar, VIB)，类比一下等额抽样 (dollar bar),

• 不等额抽样是在「不固定成交额」的前提下抽样得到。

• 等额抽样是在「固定成交额」的前提下抽样得到。

 

DIB 抽样的集合为

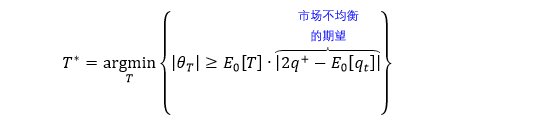
同理，市场不均衡的预期用 U = |2q⁺ - E₀[q_t]| 来量化，U 越大市场越不均衡。当 |θ_T| 比预期更加不均衡，T 越小这种情况越容易发生 (E₀[T] 越小)，这时抽样也就越频繁。

TIB, VIB, RIB 展示

使用 mlfinlab 里面的 API。

• get_dollar_imbalance_bars: DIB

• get_volume_imbalance_bars: VIB

• get_tick_imbalance_bars: TIB

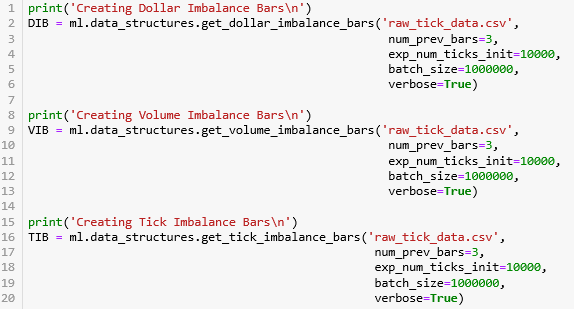
计算这些 IB 有个问题需要注意，因为要根据历史数据计算 T, b, b·v, b·q 的 EMA 值，那么第一个 bar 之前没有数据，因此我们要给一定 exp_num_ticks_init 作为第一个 bar 包含 tick 的期望数。此外我们定义用 num_prev_bars 来当 EMA 的窗口。

我们用 PyEcharts 来可视化 TIB, VIB 和 DIB，并只展示 DIB 的代码为例，其它 IB 的代码只用将 DataFrame DIB 改为 TIB 和 VIB (包括下节的 TRB, VRB 和 DRB)。

from pyecharts import Line, Kline, Bar, Grid

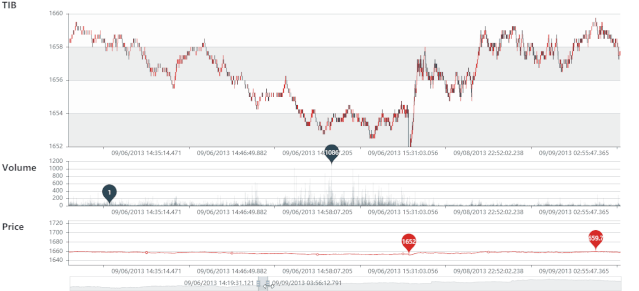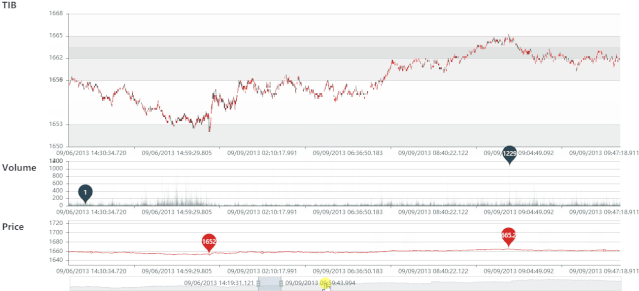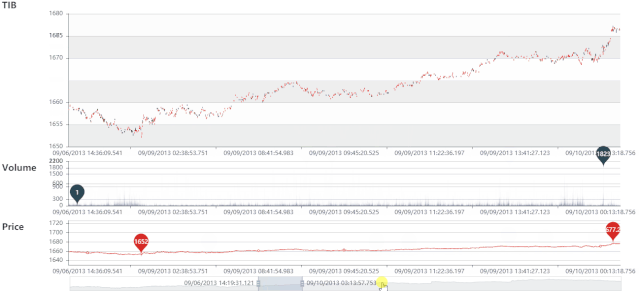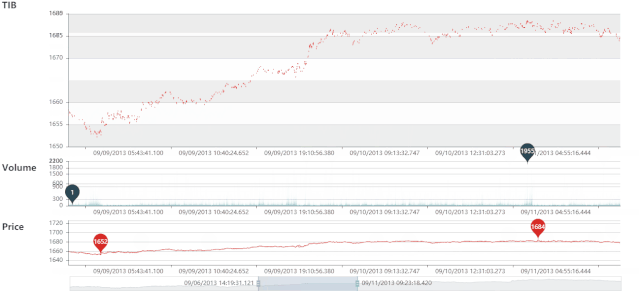
TIB, VIB 和 DIB 和动态图和静态图展示如下：

TIB 静态图

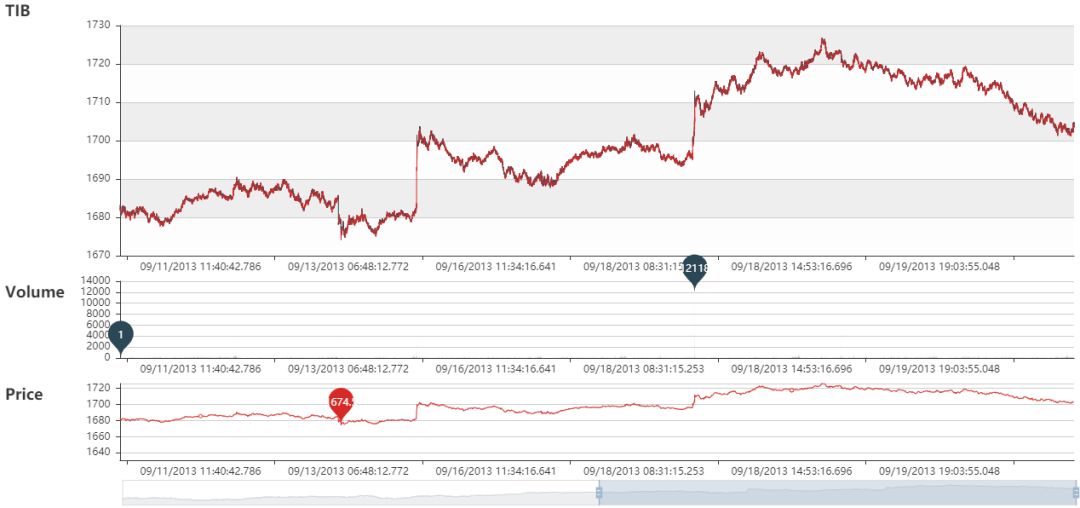
TIB 动态图

VIB 静态图

VIB 动态图

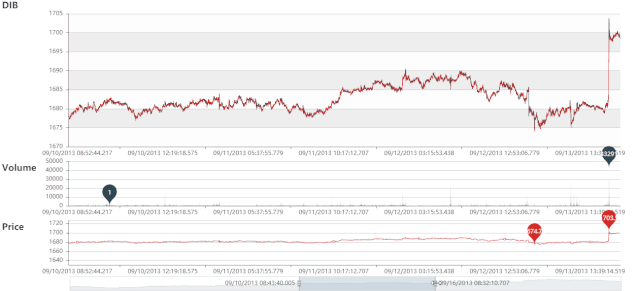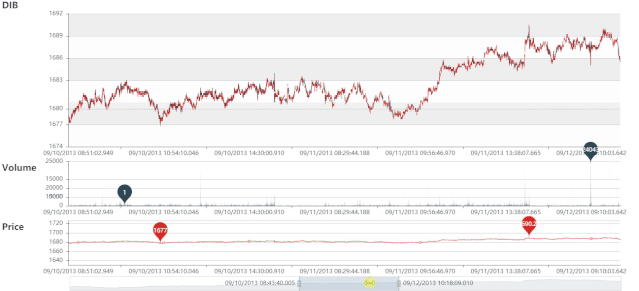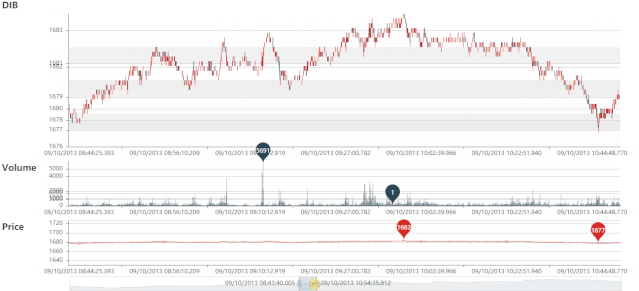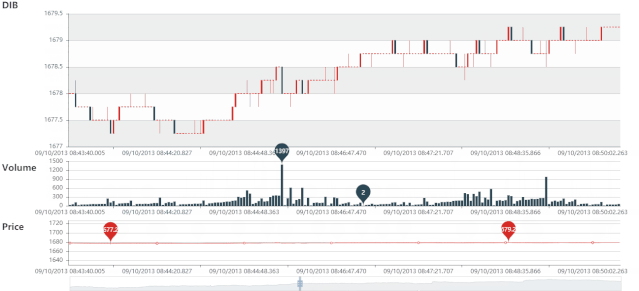
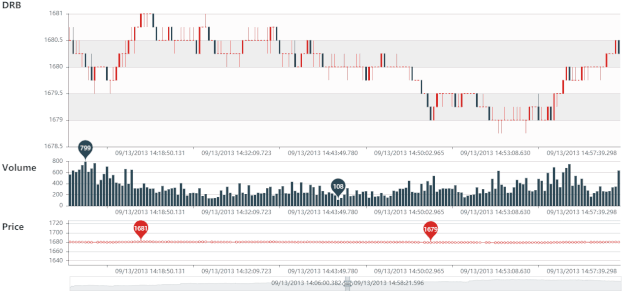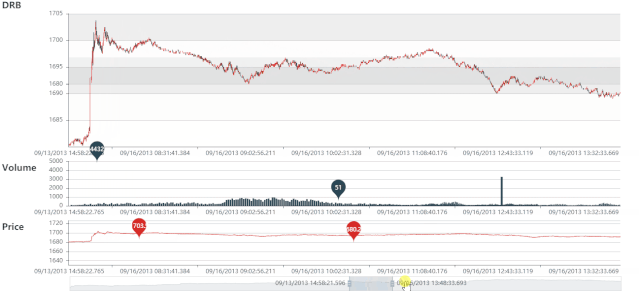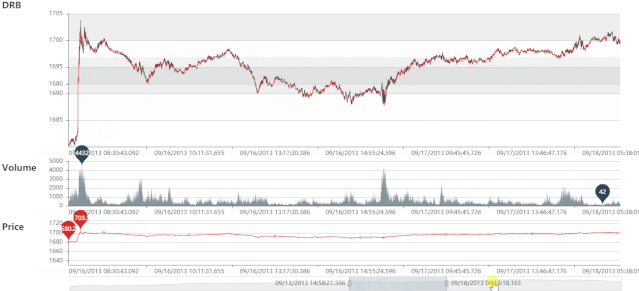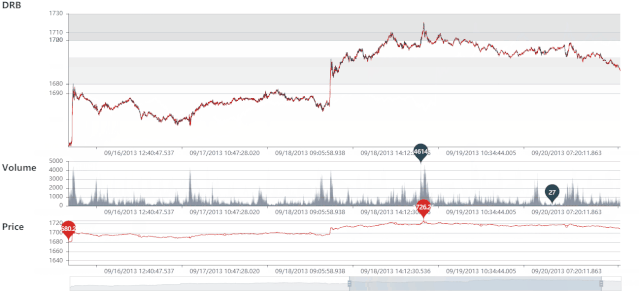
DIB 静态图

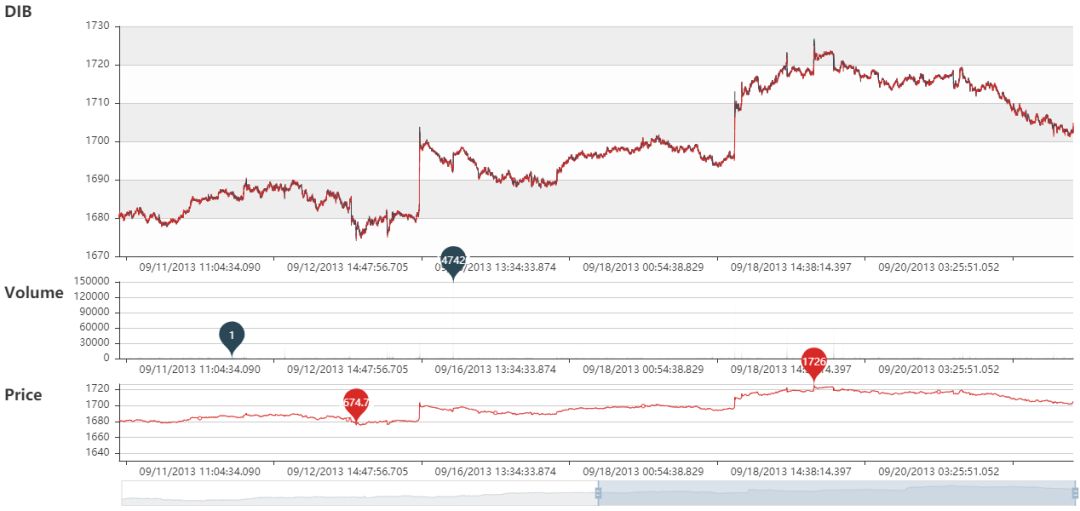
DIB 动态图

3.3

Runs Bars

IB (inbalance bars) 和 RB (runs bars) 都是以不固定笔数、不固定成交量、不固定成交额的方式来抽样，但它们的区别在于

• IB 统计了 b_t 的总和

• RB 统计了 b_t= 1 和 b_t= -1 数量的最大值

类比 TIB, VIB 和 DIB 我们定义 TRB, VRB 和 DRB。

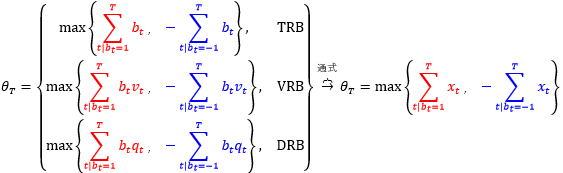
为了简化公式，令 P⁺= P(b_t= 1) 和 P^–= P(b_t= -1)，推导阈值 E₀[θ_T] 为

在实操中

• E₀[T] = 历史数据 T 的 EMA

• P⁺ = 历史数据「买单占比」的 EMA

• P^– = 历史数据「卖单占比」的 EMA

• v⁺ = 历史数据「买单占比」乘以「买单成交量」的 EMA

• v^– = 历史数据「卖单占比」乘以「卖单成交量」的 EMA

• q⁺ = 历史数据「买单占比」乘以「买单成交额」的 EMA

• q^– = 历史数据「卖单占比」乘以「卖单成交额」的 EMA

TRB, VRB, DRB 展示

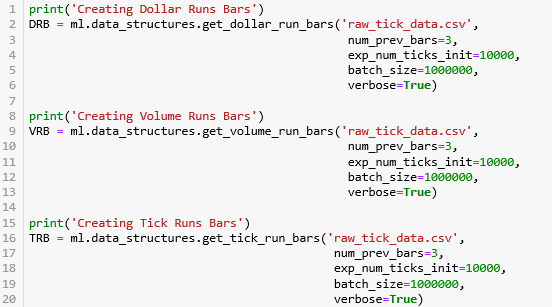
使用 mlfinlab 里面的 API：

• get_dollar_run_bars: DRB

• get_volume_run_bars: VRB

• get_tick_run_bars: TRB

打印出 IBs 和 RBs 的大小，发现 RBs 中数据个数远小于 IBs 的中数据个数 (这些个数和 num_prev_bars, exp_num_ticks_init 之类的超参数有关，而且比较敏感)。

print( DIB.shape[0], DRB.shape[0] )print( VIB.shape[0], VRB.shape[0] )print( TIB.shape[0], TRB.shape[0] )

70589 24924
75057 26184
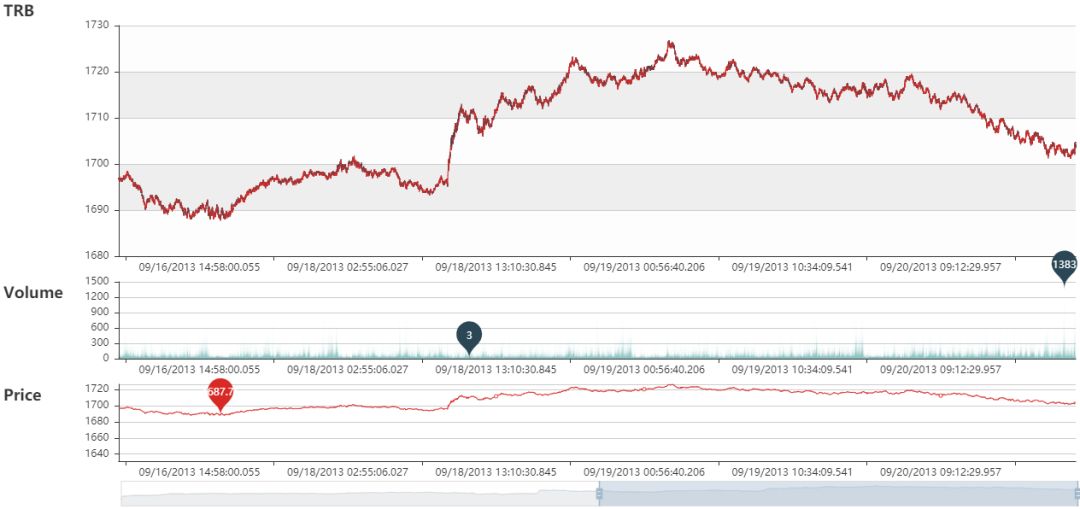
524973 201919

TRB, VRB 和 DRB 和动态图和静态图展示如下：

TRB 静态图

TRB 动态图

VRB 静态图

VRB 动态图

DRB 静态图

DRB 动态图

4总结

本节主要将如果从 tick 数据抽样到 bar 数据，大方向上有两种方法：

1. 标准法：等时抽样、等笔抽样、等量抽样、等额抽样

   
   

2. 信息驱动法：

   
   

   1. Imbalance 抽样，满足条件

      |Imbalance| ≥ Expected Imbalance

      
      

   2. Runs 抽样，满足条件

      |Run| ≥ Expected Run

道理不难，但真正实操起来坑很多，比如：

1. 数据量太大，运行时间太长。

   
   

2. 画出来的图和 Prado 书上不太一样 (看不出 dollar bar 最稳定)，光看图不行，还需要用具体的统计指标来证明 dollar bar 最稳定。

   
   

3. 抽样 IB 和 RB 需要超参数，这些参数怎么改没有一个明确的规则，我也是慢慢试出来的，而且发现每次抽样的结果对超参数非常敏感。

哎，慢慢填吧，难才好玩，难而且被功课了才有价值。

Stay Tuned！

王的机器

机器学习、金融工程、量化投资的干货营；快乐硬核的终生学习者。