LeetCode 1361. 验证二叉树【二叉树,DFS或BFS或并查集】1464

本文主要是介绍LeetCode 1361. 验证二叉树【二叉树,DFS或BFS或并查集】1464，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

本文属于「征服LeetCode」系列文章之一，这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁，本系列将至少持续到刷完所有无锁题之日为止；由于LeetCode还在不断地创建新题，本系列的终止日期可能是永远。在这一系列刷题文章中，我不仅会讲解多种解题思路及其优化，还会用多种编程语言实现题解，涉及到通用解法时更将归纳总结出相应的算法模板。

为了方便在PC上运行调试、分享代码文件，我还建立了相关的仓库：https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中，你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等，还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解，还可以一同分享给他人。

由于本系列文章的内容随时可能发生更新变动，欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。

二叉树上有 n 个节点，按从 0 到 n - 1 编号，其中节点 i 的两个子节点分别是 leftChild[i] 和 rightChild[i]。

只有 所有 节点能够形成且 只 形成 一颗 有效的二叉树时，返回 true；否则返回 false。

如果节点 i 没有左子节点，那么 leftChild[i] 就等于 -1。右子节点也符合该规则。

注意：节点没有值，本问题中仅仅使用节点编号。

示例 1：

输入：n = 4, leftChild = [1,-1,3,-1], rightChild = [2,-1,-1,-1]
输出：true

示例 2：

输入：n = 4, leftChild = [1,-1,3,-1], rightChild = [2,3,-1,-1]
输出：false

示例 3：

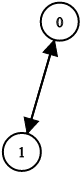
输入：n = 2, leftChild = [1,0], rightChild = [-1,-1]
输出：false

示例 4：

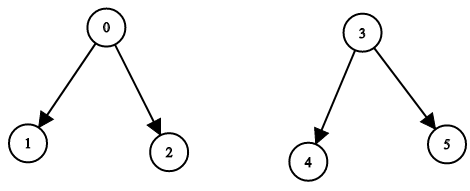
输入：n = 6, leftChild = [1,-1,-1,4,-1,-1], rightChild = [2,-1,-1,5,-1,-1]
输出：false

提示：

• 1 <= n <= 10^4
• leftChild.length == rightChild.length == n
• -1 <= leftChild[i], rightChild[i] <= n - 1

---

解法 DFS/BFS

我们将验证二叉树的过程分为两步：第一步找到二叉树的根节点，第二步从根节点开始对二叉树进行遍历，判断其是否为一颗有效的二叉树。

在第一步中，为了找到根节点，我们需要用数组 $isRoot$ 存放所有节点是否有父节点——这是因为只有入度为 $0$ 的点（即没有父节点的点）才能是根节点。同时计算边的数目。

• 我们遍历数组 $leftChild$ 和 $rightChild$ ，如果数组中的某个元素 $x$ 不为 $-1$ ，那么就表示有一条边指向节点 $x$ ，节点 $x$ 的 $isRoot[x]$ 为 $false$ 。
• 在遍历完数组 $leftChild$ 和 $rightChild$ 后，如果发现边数不为 $n-1$ ，则一定不是树。
• 如果边数为 $n-1$ ，我们再在数组 $isRoot$ 中找到一个满足 $isRoot[root]==true$ 的节点 $root$ ，即为二叉树的根节点。
• 如果有多个满足条件的节点呢？在这种情况下，这 $n$ 个节点一定不是一颗有效的二叉树。

在第二步中，我们从根节点开始进行深度优先搜索或广度优先搜索，判定这 $n$ 个节点的连通性，这是因为当这个 $n$ 个节点是一颗有效的二叉树时，所有的节点会恰好被遍历一次。如果某一个节点被遍历了超过一次（有不止一个父节点）或零次（不连通），那么这 $n$ 个节点都不是一颗有效的二叉树。由于如下说明，我们只需证明其连通即可。

对于一个包含 $n$ 个节点 $m$ 条边的无向图，如果它是一棵树，那么必须满足以下三个条件中的两个：

• $m=n-1$ ；
• 该无向图连通；
• 该无向图无环。

事实上，只要满足其中的两个条件，就可以推出第三个条件。证明不是本题的重点，因此这里不再赘述。

可以发现，第二个条件「该无向图连通」和第三个条件「该无向图无环」都需要我们对至少整个图进行一次遍历，因此只统计图的出入度、边数等信息而不对整个图进行遍历的所有算法都是错误的。并且由于本题是有向图，和无向图不同的是，有向图中仅有一个节点可以作为树的根节点（而无向图中任意一个节点都可以作为树的根节点），因此我们还需要对根节点的唯一性进行判定。那么对应到本题中：

• 第一个条件 $m=n-1$ ：统计数组 $leftChild$ 和 $rightChild$ 中非 $-1$ 的元素个数即为 $m$ ；
• 另一个条件可以考虑验证剩下两个条件中的任意一个：
  • 如果选择第二个条件「该无向图连通」，那么可以使用搜索遍历的方式来判断（例如上面给出的代码）；
  • 如果选择第三个条件「该无向图无环」，那么可以使用并查集的方式来判断。

这里，我们使用一个布尔数组 $vis$ 来存放所有被遍历过的节点，如果在搜索时遍历到某个节点，就标记该节点可访问。如果在搜索完成后，$vis$ 中有节点没被访问，那么说明这 $n$ 个节点不连通。

class Solution {
public:bool validateBinaryTreeNodes(int n, vector<int>& leftChild, vector<int>& rightChild) {vector<bool> isRoot(n, true);int edges = 0;for (int i = 0; i < n; ++i) {if (leftChild[i] != -1) {isRoot[leftChild[i]] = false;++edges;}if (rightChild[i] != -1) {isRoot[rightChild[i]] = false;++edges;}}// 从根结点连通,n个点,n-1条边if (edges != n - 1) return false;// 只有1个根结点int roots = 0, root = -1;for (int i = 0; i < n; ++i) if (isRoot[i]) { root = i; ++roots; }if (roots != 1) return false; // 其实可在连通性判断中处理多根情况queue<int> q;q.push(root);vector<bool> vis(n);while (!q.empty()) {int u = q.front();vis[u] = true;q.pop();if (leftChild[u] != -1) q.push(leftChild[u]);if (rightChild[u] != -1) q.push(rightChild[u]);}for (int i = 0; i < n; ++i) if (vis[i] == false) return false;return true;}
};

复杂度分析：

• 时间复杂度：$O(N)$ 。
• 空间复杂度：$O(N)$ 。

本题的测试数据非常弱，这会导致一些错误的算法可以通过所有的数据。我们必须注意到这些错误的算法。

这篇关于LeetCode 1361. 验证二叉树【二叉树,DFS或BFS或并查集】1464的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---