海明码，奇偶校验码

1.奇偶校验码

用于检查二进制传输后有没有出错。
在需要传的二进制数据前再加一位校验位。分两种校验方法：奇校验，偶校验。

奇校验：保证这段数据有奇数个1
比如：0101——>前头添加一个1——>10101
偶校验：保证这段数据有偶数个1
比如：0101——>前头添加一个0——>00101

这样，以奇校验为例，当10101准确无误传过去之后，电脑一看，1开头，再数数整个编码1的个数，是奇数个，那计算机就认为没错了。

但是，很容易想到，这个校验方法太宽松了。要是10101传过去之后变成了10110有偶数个二进制位发生错误。但是整个编码还是奇数个1，所以计算机判别不出来。（因为奇数加减偶数等于奇数，偶数加减偶数等于偶数。奇偶不变。）

所以无论奇校验还是偶校验，都只能检验出奇数个位数出错，毕竟奇数加减奇数等于偶数，偶数加减奇数等于奇数。相比原来的奇偶都变了。

码距：一个编码系统中任意两个不同的合法编码之间至少有多少个二进制为不同。
奇偶校验码的码距为2，为什么呢？

因为对于奇偶校验码来说，任意两个校验码之间，如果想不同，最少变换两个位置的码元才可以完成。
比如对于10011（奇校验）来说，如果我任意反转一个码元，1的个数肯定为偶数个，所以我至少需要反转两个码元才可以是另一个奇校验码。而反转的这个数字就是奇校验码的码距。（以上深黑色字体引于百度 不回起名字咋办 账户的解释）

2.海明码

2.1列题引入

学海明码时，我就感觉越学越像某道智力题，它的解法其实就是海明码的思路。那就是有名的老鼠尝毒。
题目：
有 1000 瓶药物，但是其中有一瓶是有毒的，老鼠只要服用任意量有毒药水就会在一个星期内死掉！请问，如何用10只小白鼠在一个星期后找出有毒的药物？

解法很简单，当初出这个题的人应该就学过海明码。
首先，给这1000瓶药物用二进制编码

（图片引用于2021dragon的博文）
有毒的药水就在这1000瓶之中。它也有相应编码。

然后，让1号老鼠把编码最后一位都为1的喝掉。如果有毒药水编码的最后一位为1，那么1号老鼠就嗝屁了，也就是说，如果1号死了，说明有毒药水的编号最后一位是1，如果1号没死，说明有毒药水的编号最后一位是0。

同样的操作，分别让第n号老鼠喝下倒数第n位编码是1的药水。这样就可以通过10只老鼠的死活判断出有毒药水的编码，也就找到了有毒药水。

n只老鼠，最大可以判断2ⁿ瓶药水中哪瓶有毒。

2.2海明码详细讲解

那么回到海明码。如果你懂了上面的耗子尝毒，你就很容易理解了。

首先，海明码也要运用奇偶校验码，这里都以偶校验为例子。海明码是用x位校验码，把k位数据分组。

其实这里的校验码就和耗子尝毒里的耗子的作用一样。但是规则更加多。

首先，把数据块的每一位都编上号码，数据位就像耗子尝毒里的瓶子。不过在海明码里，是要把耗子和瓶子放在一起编码，并且耗子要放在2的i次方的地方（0001，0010，0100，1000…）

注意，海明码编码时，所有瓶子都没毒的，让耗子按规矩获得数值。

发送数据时，先占着校验位，然后空着的位填你想发的数据。

以1010110为例
（图片引用于夜风~大佬的博文http://t.csdn.cn/8nSQi）
x1,x2,x3,x4就是放校验码（放耗子）的地方。

那么如何计算校验码的值？
让x1耗子尝所有编码最后一位为1的瓶子，可以看到编码最后一位为1（0011，0101，0111，1001，1011）的瓶子，内容分别为1，0，0，1，0
因为每一组用的是偶校验，所以
x1⊕1⊕0⊕0⊕1⊕0=0

关于异或⊕
1.异或是相异为1，相同为0。
2.一个数异或0还是它本身。因为如果该位为0，异或为0的相应位，相同为0，如果该位为1，异或为1的相应位，相异为1。所以一个数异或0后二进制哪一位都没变，所以异或0后还是它本身。
3.一个数异或它自己等于0，异或相同为0嘛。

回到x1⊕1⊕0⊕0⊕1⊕0=0
因为是偶校验，所以需要保证偶数个1，0不用管，反正异或了也没变。而偶数个1异或自然等于0。
这就是x1⊕1⊕0⊕0⊕1⊕0=0的由来

用同样的方法可得
x1=0
x2=1
x3=1
x4=0

所以，最后的海明码就是

（图片引用于夜风~大佬的博文http://t.csdn.cn/8nSQi）

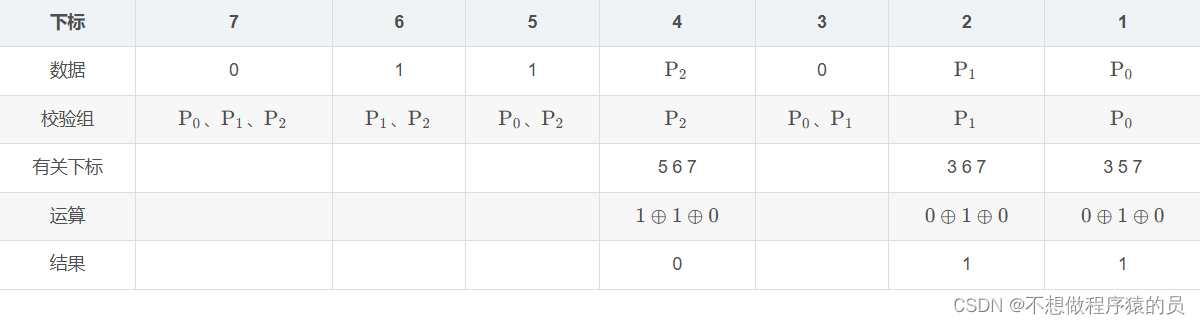
海明码的校验
如果说最后一个位置1011因为数据传输错误，0变成了1，也就是编号为1011的瓶子的药水突然有毒了。

那么让所有耗子都去尝他们负责的瓶子药水（0001耗子尝编码最后一位为1的药水，0010尝编码倒数第二位为1的药水，以此类推）。
在数据没出错之前，耗子尝完它需要尝的瓶子药水，结果都为0（因为是偶校验，所以需要保证偶数个1，0不用管，反正异或了也没变。而偶数个1异或自然等于0。
这就是x1⊕1⊕0⊕0⊕1⊕0=0的由来）。

但是现在1011的0变成了1，也就是1000耗子，0010耗子，0001耗子都要比之前多尝一个1了，也就是多异或一个1了。那原来的0多异或一个1，当然就变成1了。

xxx1:0⊕1⊕0⊕0⊕1⊕1=1
xx1x:1⊕1⊕1⊕0⊕1⊕1=1
x1xx:1⊕0⊕1⊕0=0
1xxx:0⊕1⊕1⊕1=1

结果从下往上看，从高位到低位写。
这样出错的位置也就出来了。1011。

这里耗子和瓶子药水一样，都可以出问题，无论哪个出问题，都可以检查出来。因为他们的异或为1了。

2.3海明码校验码位数问题

设数据有n位，校验码有x位。则校验码一共有2^x种取值方式。其中需要一种取值方式表示数据正确，剩下2^x−1种取值方式表示有一位数据出错。因为编码后的二进制串有n+x位，因此x应该满足：2^x−1≥n+x　　　（2.3海明码校验码位数问题取自夜风~大佬的博文解释http://t.csdn.cn/8nSQi）