本文主要是介绍图形学学习 TOPIC 3 3D Viewing Implementation,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
- 一、Classical Viewing(经典/人眼观察)
- 平面几何投影
- 1.平行投影 parellel
- (1)正投影 orthographic projection
- (2)轴测投影 axonometric projection
- (3)斜投影 oblique projection
- 2.透视投影
- 二、Computer Viewing
- 1.平行投影
- (1)正投影(正交投影):orthographic projection
- Summary
- (2)斜投影
- 2.透视投影
- 透视投影规范矩阵
一、Classical Viewing(经典/人眼观察)
Classical Viewing 需要三个基本要素
(1)一个或多个观察对象
(2)观察者和一个投影表面
(3)从物体到投影表面的投影仪
投影中心:照相机镜头或者人眼中心(COP)
透视投影:COP在有限远处
平行投影:COP在无限远处
平面几何投影:投影面是平面 & 投影线是直线
平面几何投影
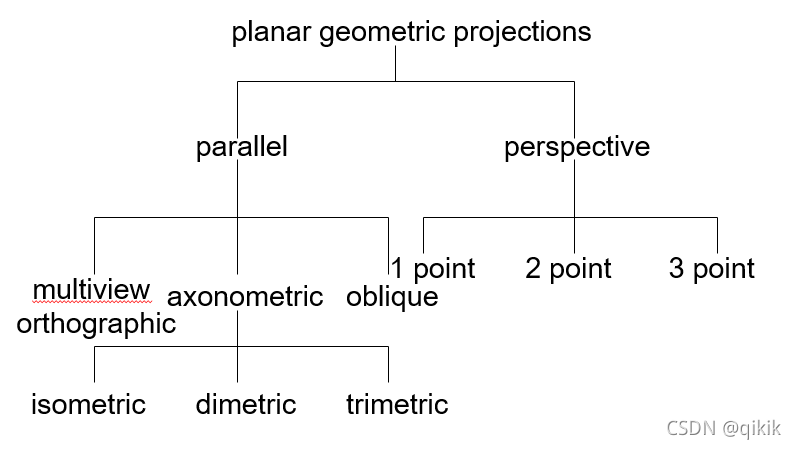
1.平行投影 parellel
投影线之间是平行的
(1)正投影 orthographic projection
(1)投影线和投影平面垂直
(2)投影平面平行于对象的某个主面
(3)不改变距离和角度
eg:三视图
(2)轴测投影 axonometric projection
(1)投影线和投影平面垂直
(2)投影平面相对于对象的方向可以任意
等轴侧投影:投影平面相对于三个主面对称:三轴向的比率都相同
正二测投影:投影平面相对于两个主面对称:两轴向比率相同
正三测投影:三轴向比率均不相同
(3)斜投影 oblique projection
(1)允许投影线和投影平面成任意角度
2.透视投影
非均匀透视缩短(nonuniform foreshortening):
投影后尺寸会缩短:即对象距离观察者越远,它所成的像越小,非等距缩小
一点、两点、三点透视:区别在于对象的三个主方向中有几个平行于投影平面。
三点:没有平行于投影平面的主方向,沿着每个主方向的平行线相交于有限远处的灭点(Vanishing Points)。
两点:允许一个主方向平行于投影平面,其余沿着两个主方向的平行线相交于灭点
一点:允许两个主方向平行于投影平面,因而只要一个灭点。
二、Computer Viewing
Computer Viewing 的viewing process需要三个基本要素
(1)照相机的位置
(2)选择一个镜头(设置投影矩阵)
(3)剪裁(设置视体)
1.平行投影
投影的规范化: 先把对象变形(规范化矩阵),使得变形后的对象的正交投影图与原来想要得到的对象的投影图相同
平行投影: → \rightarrow → 规范化 → \rightarrow → 正投影
(1)正投影(正交投影):orthographic projection
投影线垂直于观察平面
投影平面为 z=0
P p = M o r t h I P [ x p y p z p 1 ] = [ 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 ] [ x y z 1 ] \bm{P_p}=\bm{M_{orth}}\bm{I}\bm{P} \\ \begin{bmatrix} x_p \\ y_p \\ z_p \\ 1\\ \end{bmatrix}= \begin{bmatrix} 1 &0 & 0& 0 \\ 0 & 1 &0 &0\\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}\begin{bmatrix} x \\ y \\ z \\ 1\\ \end{bmatrix} Pp=MorthIP⎣⎢⎢⎡xpypzp1⎦⎥⎥⎤=⎣⎢⎢⎡1000010000000001⎦⎥⎥⎤⎣⎢⎢⎡xyz1⎦⎥⎥⎤
其中 I I I为 4 × 4 4\times4 4×4的单位矩阵。
此时只有位于 “棱边长度为2,以坐标原点为中心的正方体”(规范视见体) 内的对象才有可能成像。
如果希望控制 对象与裁剪体的位置关系并确定对象的可见性,那么我们可以使用几何变换矩阵N代替单位矩阵 I I I
方法:把ortho创建的一个正交平行的视景体映射成规范视见体
mat4 N=Ortho(left,right,bottom,top,near,far);
(注意0<near<far)
总共需要两个变换:
①平移,把指定视见体的中心移动到规范视见体的中心
②缩放:使每条边的长度都为2
T = T ( − ( r i g h t + l e f t ) 2 , − ( t o p + b o t t o m ) 2 , + ( f a r + n e a r ) 2 ) S = S ( 2 ( r i g h t − l e f t ) , 2 t o p − b o t t o m ) , 2 ( n e a r − f a r ) ) N = S T = [ 2 r i g h t − l e f t 0 0 − r i g h t + l e f t r i g h t − l e f t 0 2 t o p − b o t t o m 0 − t o p + b o t t o m t o p − b o t t o m 0 0 2 n e a r − f a r − f a r + n e a r f a r − n e a r 0 0 0 1 ] \bm{T}=\bm{T}(\frac{-(right+left)}2,\frac{-(top+bottom)}2,\frac{+(far+near)}2)\\ \quad \\ \bm{S}=\bm{S}(\frac{2}{(right-left)},\frac{2}{top-bottom)},\frac{2}{(near-far)})\\ \quad \\ \bm{N}=\bm{S}\bm{T}=\begin{bmatrix} \frac{2}{right-left} &0 & 0& -\frac{right+left}{right-left} \\ \\ 0 & \frac{2}{top-bottom} &0 & -\frac{top+bottom}{top-bottom} \\ \\ 0 & 0 & \frac{2}{near-far} & -\frac{far+near}{far-near} \\ \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} T=T(2−(right+left),2−(top+bottom),2+(far+near))S=S((right−left)2,top−bottom)2,(near−far)2)N=ST=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡right−left20000top−bottom20000near−far20−right−leftright+left−top−bottomtop+bottom−far−nearfar+near1⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
Summary
投影平面是z=0 : 先变换视见体,再进行正投影。即: P p = M o r t h S T P \bm{P_p}=\bm{M_{orth}}\bm{ST}\bm{P} Pp=MorthSTP
(2)斜投影
先把对象变形,使 要求的投影 转换为 变形后的对象的规范正交 投影。
P p = M o r d h S T H ( θ , ϕ ) P \bm{P_p}=\bm{M_{ordh}}\bm{STH}(\theta,\phi)\bm{P} Pp=MordhSTH(θ,ϕ)P
其中 M o r d h S T \bm{M_{ordh}}\bm{ST} MordhST都同正投影一样,那么主要目标就在于获得矩阵 H ( θ , ϕ ) \bm{H(\theta,\phi)} H(θ,ϕ)
(这里注意一点,ST中的left right bottom top对应于斜投影视见体经过H变换之后得到的长方体顶点 )

下图:左图为上图的俯视图,右图为上图的右视图
 H ( θ , ϕ ) = [ 1 0 c o t θ 0 0 1 c o t ϕ 0 0 0 1 0 0 0 0 1 ] \bm{H}(\theta,\phi)= \begin{bmatrix} 1 &0 & cot\theta & 0 \\ 0 & 1 &cot\phi &0\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}\\ H(θ,ϕ)=⎣⎢⎢⎡10000100cotθcotϕ100001⎦⎥⎥⎤
H ( θ , ϕ ) = [ 1 0 c o t θ 0 0 1 c o t ϕ 0 0 0 1 0 0 0 0 1 ] \bm{H}(\theta,\phi)= \begin{bmatrix} 1 &0 & cot\theta & 0 \\ 0 & 1 &cot\phi &0\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}\\ H(θ,ϕ)=⎣⎢⎢⎡10000100cotθcotϕ100001⎦⎥⎥⎤
其中的 θ 、 ϕ \theta、\phi θ、ϕ 由斜投影的投影线方向和投影平面所成的夹角给出
2.透视投影
假设照相机(COP)在原点,方向指向z轴负方向
将投影平面放在投影中心的前面,此时空间中的一点 ( x , y , z ) (x,y,z) (x,y,z)沿着一条投影线被投影到 ( x p , y p , z p ) (x_p,y_p,z_p) (xp,yp,zp)。所有的投影线都经过COP。
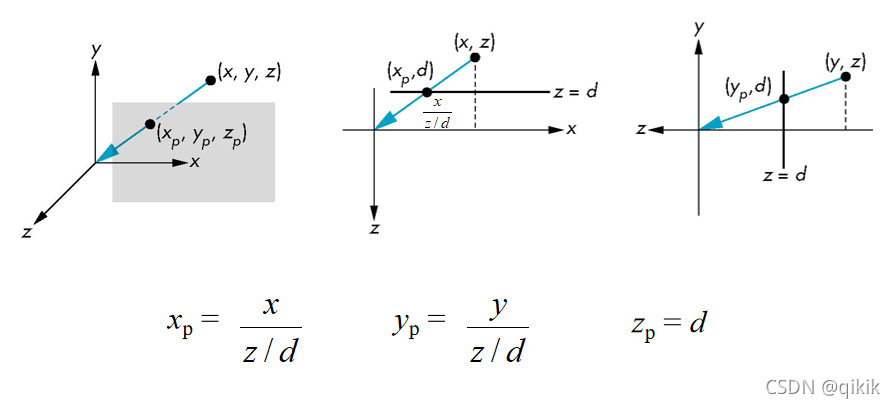
可以看出在推出的 ( x p , y p , z p ) (x_p,y_p,z_p) (xp,yp,zp)中,是非均匀的透视缩短,即对象离投影中心越远,所成的像越小。
这类投影是不可逆的:即一条投影线上所有的点都会投影到同一个点,我们不能从一个点的投影恢复出这个点。
q ′ = q = M p [ x z / d y z / d d 1 ] = [ x y z z / d ] = [ 1 0 0 0 0 1 0 0 0 0 1 0 0 0 1 / d 0 ] [ x y z 1 ] \bm{q'}=\bm{q}=\bm{Mp}\\ \begin{bmatrix} \frac{x}{z/d} \\ \frac{y}{z/d} \\ d \\ 1\\ \end{bmatrix}=\begin{bmatrix} x \\ y \\ z \\ z/d\\ \end{bmatrix}= \begin{bmatrix} 1 &0 & 0& 0 \\ 0 & 1 &0 &0\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 1/d & 0 \\ \end{bmatrix}\begin{bmatrix} x \\ y \\ z \\ 1\\ \end{bmatrix} q′=q=Mp⎣⎢⎢⎡z/dxz/dyd1⎦⎥⎥⎤=⎣⎢⎢⎡xyzz/d⎦⎥⎥⎤=⎣⎢⎢⎡100001000011/d0000⎦⎥⎥⎤⎣⎢⎢⎡xyz1⎦⎥⎥⎤
透视投影规范矩阵
首先,对于投影平面z=-1,并且投影中心位于原点的透视投影,我们已知投影变换矩阵为:
M = [ 1 0 0 0 0 1 0 0 0 0 1 0 0 0 − 1 0 ] \bm{M}= \begin{bmatrix} 1 &0 & 0& 0 \\ 0 & 1 &0 &0\\ 0 & 0 & 1 & 0 \\ 0 & 0 & -1 & 0 \\ \end{bmatrix} M=⎣⎢⎢⎡10000100001−10000⎦⎥⎥⎤
我们将该投影平面移到z=0,此时即对当前投影进行正投影,即乘 M o r t h \bm{M_{orth}} Morth,最终变换矩阵为:
[ 1 0 0 0 0 1 0 0 0 0 0 0 0 0 − 1 0 ] \begin{bmatrix} 1 &0 & 0& 0 \\ 0 & 1 &0 &0\\ 0 & 0 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ \end{bmatrix} ⎣⎢⎢⎡10000100000−10000⎦⎥⎥⎤
下面,我们使用新方法得到同样的变换矩阵:
假定视见体侧面和投影平面夹角为45°
先应用变换 N N N,再应用正交投影,得到的结果与上面相同:
( N N N的作用即为得到一个规范视见体:将半无穷棱锥变为规范视见体)
d = − n e a r N = [ 1 0 0 0 0 1 0 0 0 0 α β 0 0 − 1 [ 1 / d ] 0 ] α = n e a r + f a r n e a r − f a r β = 2 × n e a r × f a r n e a r − f a r 0 < n e a r < f a r d=-near\\ \bm{N}= \begin{bmatrix} 1 &0 & 0& 0 \\ 0 & 1 &0 &0\\ 0 & 0 & \alpha & \beta \\ 0 & 0 & -1[1/d] & 0 \\ \end{bmatrix}\\ \quad\\ \alpha=\frac{near+far}{near-far}\\ \quad\\ \beta=\frac{2\times near\times far}{near-far}\\ \quad\\ 0<near<far d=−nearN=⎣⎢⎢⎡1000010000α−1[1/d]00β0⎦⎥⎥⎤α=near−farnear+farβ=near−far2×near×far0<near<far
若投影平面z=d
假定视见体侧面和投影平面夹角为 θ \theta θ
则推导思路为:
本质思想为,得到一个矩阵N,使变换N后所得即为规范视见体
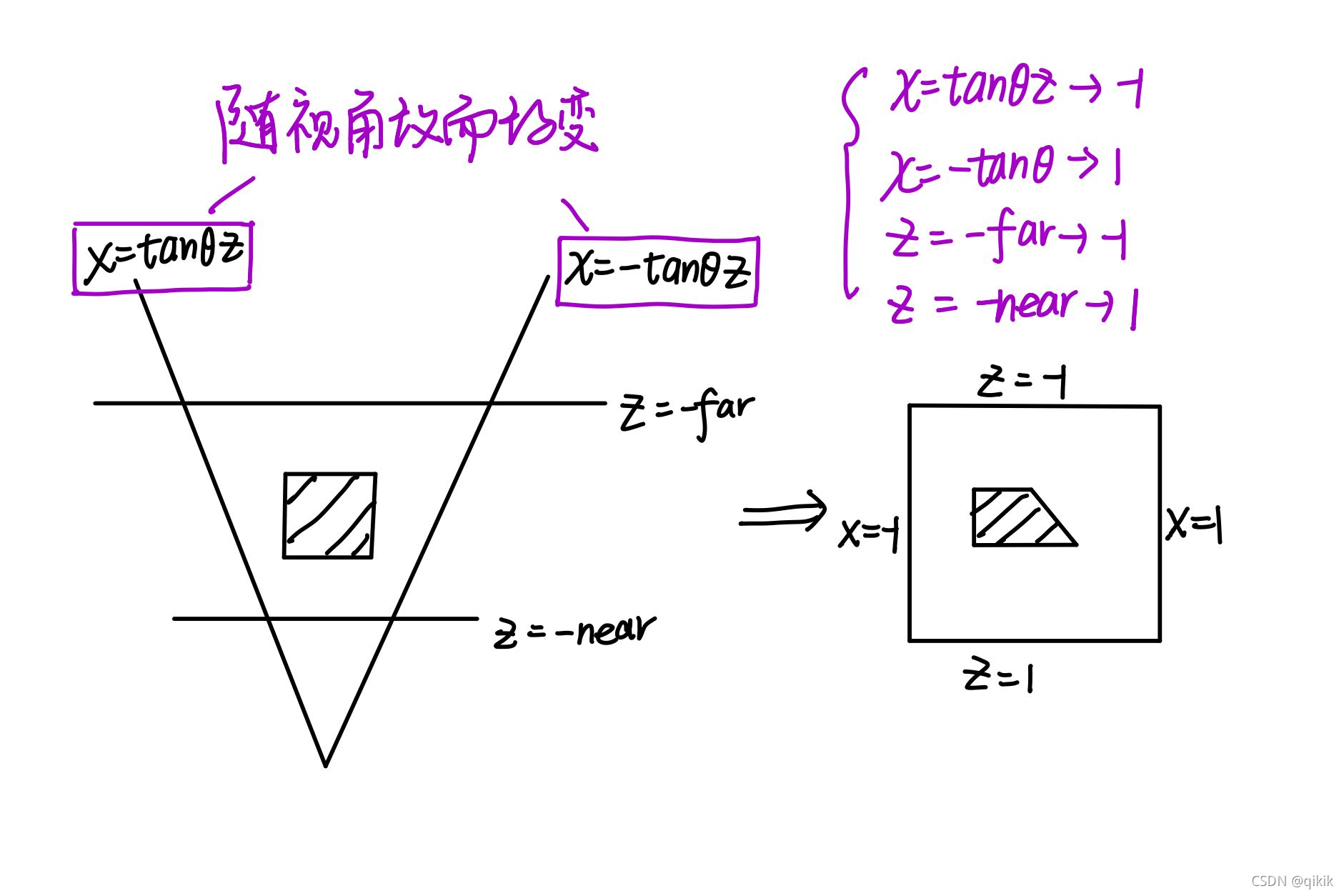
这篇关于图形学学习 TOPIC 3 3D Viewing Implementation的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







