堆和优先级队列 下沉 上浮 最大堆

堆和优先级队列（内部就是堆）

堆（二叉堆 基于二叉书的堆）

二叉堆：一颗完全二叉树 结构上：完全二叉树

堆中根节点》=子树中的节点值（最大堆、大根堆）小根堆相反；且在堆中只能保证当前节点和和子节点以及父节点之间的大小关系 和层次无关

完全二叉树建议使用顺序表（数组）存储：没有空间的浪费 使用顺序表存储时 如果根节点从0开始排序那么它的子节点就是2k+1 和2k+2一般只需要判断左树就行当2k+1<arr.length;

当判断一个节点的父节点是否存在？只需判断它是否为根节点 换个说法就是判断父节点编号是否>=0即可 父节点的索引为（k-1）>>1  或者只需要看k是否大于0

当我想给最大堆中添加一个新元素 我可以直接在数组的末尾新增元素，再调整结构（siftup）保证为最大堆，

元素上浮的终止条件

1已经走到根节点

2已经走到比父节点小的位置

siftUp(int k);//向上调整为索引为k的节点，使其仍然满足堆的性质

package heap;import java.util.ArrayList;
import java.util.List;/*** @author hututu* @date 2022/03/29 18:00**/
public class MaxHeap {//使用JDK的动态数组arraylist来储存一个最大堆//list数组的add方法默认是尾插List<Integer> data;public MaxHeap(){this(10);}public MaxHeap(int size){data=new ArrayList<>(size);//数组初始化}public  void add(int i){data.add(i);siftUp(data.size()-1);}public boolean isEmpty(){return data.size()==0;}public  void siftUp(int k){//1已经走到根节点k<0或者//2已经走到比父节点小的位置while (k>0&&data.get(k)>data.get(parent(k))){swap(k,parent(k));k=parent(k);}}private void swap(int i, int j) {int temp=data.get(i);data.set(i,data.get(j));data.set(j,temp);}//根据索引得到父节点的索引private  int parent(int k){return (k-1)>>1;}private int leftChild(int k){return (k<<1)+1;}private int rightChild(int k){return (k<<1)+2;}@Overridepublic String toString() {return "MaxHeap{" +"data=" + data.toString() +'}';}
}

 对于堆而言堆顶元素就是最值，最大堆的堆顶就是最大值，要想删除一个堆顶元素分为两步，我们取出堆顶元素后，直接将数组末尾的元素顶到堆顶，然后进行下沉（siftDown）操作

这种操作方法还有一个小特别之处就是将原数组遍历完后可以得到一个非递减的数组

 下沉就是把索引为k的节点不断下沉，直到到达最终位置

下沉最终位置条件：2k+1（左子树）>size 或者 当前值>左右子树

 代码如下：

    public int extractMax(){if (isEmpty()){throw new NoSuchElementException("heap is empty! cannot extract");}int max=data.get(0);//1将数组末尾元素顶到堆顶int lastVa=data.get(data.size()-1);data.set(0,lastVa);//2数组末尾元素删除data.remove(data.size()-1);//3进行元素的下沉操作siftDown(0);return max;}private void siftDown(int k) {//当存在子树时while (leftChild(k)<data.size()){int j=leftChild(k);//判断一下是否有子树if (j+1<data.size()&&data.get(j+1)>data.get(j)){//此时存在右子树且大于左树的值j+=1;}//J为左右子树的最大值 在和当前节点K去比较if (data.get(k)>=data.get(j)){break;}else {swap(k,j);k=j;}}}

时间复杂度为nlogn 外层为n  hp.add（）为一个二叉书的高度logn

       int[] data={65,30,52,11,24,30,25,32,23};MaxHeap hp=new MaxHeap();for (int i:data) {hp.add(i);}System.out.println(hp);

heapify--堆化操作 可以将任意数组调整为堆的结构 我们可以将任意一个数组看成一个完全二叉树 从当前完全二叉树的最后一个非叶子结点进行元素的下沉操作，即可调整

为堆，时间复杂度为O（n）具体原因如下

heapify的思想就是：从小问题逐步向上走，不断去调整子树，将子树不断变为大树的过程

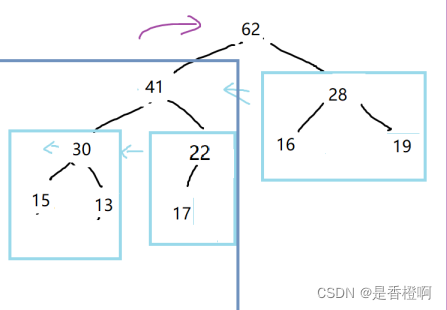
int lastNotLeafNode=parent(data.size()-1)

  public MaxHeap(int[] arr){data =new ArrayList<>(arr.length);//1先将arr的所有元素复制到data数组中for (int i:arr){data.add(i);}//2从最后一个非叶子节点开始进行siftDownfor (int i=parent(data.size()-1);i>=0;i--){siftDown(i);}}