本文主要是介绍Householder变换进行QR分解及其代码实现(C++),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 简介
- 前置理论
- Householder进行QR分解
- 代码实现
简介
初等变换工具如三角分解(LU分解)可以用于求解线性方程组,但确实存在一些限制。例如,对于病态(ill-conditioned)的线性方程组,LU分解可能会导致数值不稳定的结果。此外,对于不可逆矩阵,LU分解也不适用。
为了克服这些问题,引入了QR分解,其中矩阵分解为正交矩阵Q和上三角矩阵R。QR分解对于任何可逆矩阵都是适用的,并且可以提供数值稳定的解决方案。QR分解的实现可以借助施密特正交规范化、吉文斯变换和豪斯霍尔德变换等技术来完成。
在QR分解中,正交矩阵Q的列是正交的,这意味着它们满足Q的转置乘以Q等于单位矩阵。这种性质有助于减少数值误差的传播,并提供了数值稳定性。同时,上三角矩阵R包含了原始矩阵的重要信息,可以用于求解线性方程组等任务。
Householder变换是一种线性变换,它将一个向量投影到一个新的方向上,通常是在一个超平面上。它可以用来零化一个向量中除第一个元素外的所有元素,这使得我们可以将其用于QR分解中的反射操作。通过连续地应用一系列Householder变换,我们可以将原始矩阵A转化为上三角矩阵R。在这个过程中,我们也构建了正交矩阵Q,它将被用于最终的QR分解。
Householder变换的关键思想是找到一个反射面(或反射超平面),它可以将向量映射到零向量或某个特定方向上。这个变换的设计允许我们零化某些元素,从而实现了R的上三角形态。Householder变换在数值计算和线性代数中有广泛的应用,特别是在QR分解和特征值计算等领域。
前置理论
先看一个定理:
对任意二范数为1的向量 ω ∈ R n \omega \in {R^n} ω∈Rn,其反射矩阵为: H = I − 2 ω ω T H = I - 2\omega {\omega ^T} H=I−2ωωT,其中I为单位阵。反射阵H满足: H T = H H^{\rm{T}} = H HT=H H ∗ H = I H*H = I H∗H=I
简证:
H T = ( I − 2 ω ω T ) T = I − 2 [ ( ω T ) T ω T ] = I − 2 ω ω T {H^T} = {\left( {I - 2\omega {\omega ^T}} \right)^T} = I - 2\left[ {{{\left( {{\omega ^T}} \right)}^T}{\omega ^T}} \right] = I - 2\omega {\omega ^T} HT=(I−2ωωT)T=I−2[(ωT)TωT]=I−2ωωT
H ∗ H = ( I − 2 ω ω T ) ∗ ( I − 2 ω ω T ) = I − 2 ω ω T − 2 ω ω T + 4 ω ( ω T ω ) ω T = I − 4 ω ω T + 4 ω ω T = I H * H = \left( {I - 2\omega {\omega ^T}} \right) * \left( {I - 2\omega {\omega ^T}} \right) = I - 2\omega {\omega ^T} - 2\omega {\omega ^T} + 4\omega \left( {{\omega ^T}\omega } \right){\omega ^T} = I - 4\omega {\omega ^T} + 4\omega {\omega ^T} = I H∗H=(I−2ωωT)∗(I−2ωωT)=I−2ωωT−2ωωT+4ω(ωTω)ωT=I−4ωωT+4ωωT=I
反射变换可以理解为两向量关于一个法平面对称的过程。设超平面S(过原点,以w为法向量)即: S = { x ∣ ω T x = 0 , ∀ x ∈ R n } S = \{ x{|}{\omega ^T}x = 0,{\forall _x} \in {R^n}\} S={x∣ωTx=0,∀x∈Rn}
也就是: ∀ z , z ′ ∈ R n \forall z,z' \in {R^n} ∀z,z′∈Rn 若两向量二范数相等,则存在一个反射变换矩阵H 使 z ′ = H z z' = Hz z′=Hz z’ 与z关于超平面S对称,如下图所示。
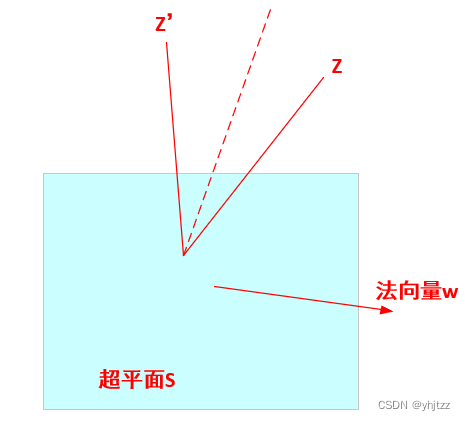
这一点比较重要,因此再通俗易懂的表达下:在一个n维空间中,只要两个向量的模相等,则可以找到一个超平面,使两向量关于该超平面对称,也就是能找到一个H使上式成立。
Householder进行QR分解
首先,我们期望将任意实阵A分解为QR 即A = Q*R,其中Q为对称正交阵,R为上三角阵。
假设待分解的矩阵A如下:
 对
对
于A中每列向量v,可以找到一个单位向量使 v → = α e → \mathop v\limits^ \to = \alpha \mathop e\limits^ \to v→=αe→,那么则可以找到H使 H v → = α e → H\overrightarrow v \ = \alpha \overrightarrow e Hv =αe
则可以将A变换为
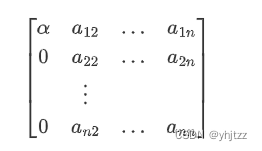
通过以上变换,第一列已经符合上三角阵,接着对第二列进行变换,此时的矩阵应该比第一次变换小一阶,如下图所示(红色部分即为待变换部分)
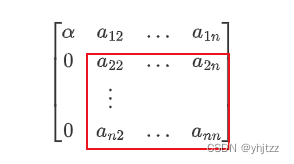
通过变换,矩阵的阶数会越来越小。所以将A变换为上三角,则可看为对A作一系列的H变换即:
H n . . . . H 3 H 2 H 1 A = R {H_n}....{H_3}{H_2}{H_1}A = R Hn....H3H2H1A=R
由于H对称正交,则 Q T = H n . . . . H 1 {Q^T} = {H_n}....{H_1} QT=Hn....H1,Q也是对称正交,则 A = Q R A = \ Q R A= QR
代码实现
算法实现过程:(第K次变换矩阵H求解如下)
v K → = A K ( A K 为子阵,长度为 ( n − k + 1 ) ) v K → = v K → − ∥ v k → ∥ ⋅ e k → v k → = v k → ∥ v ∥ H k = I − 2 v k ∗ v k T \overrightarrow {{\ v _K}} = {A_K}\left( {{A_K}为子阵,长度为(n - k + 1)} \right)\\\overrightarrow {{\ v _K}} = \overrightarrow {{\ v _K}} - \left\| {\overrightarrow {{\ v _k}} } \right\| \cdot \overrightarrow {{e_k}}\\\overrightarrow {{\ v _k}} = \frac{{\overrightarrow {{\ v _k}} }}{{\left\| \ v \right\|}}\\\ {H_k} = I - 2{\ v _k} * {\ v _k}^T vK=AK(AK为子阵,长度为(n−k+1)) vK= vK− vk ⋅ek vk=∥ v∥ vk Hk=I−2 vk∗ vkT
使用Eigen库实现
#include <iostream>
#include <vector>
#include <Eigen/Dense>
#include <Eigen/Core>
void householderQR(Eigen::MatrixXd &A, Eigen::MatrixXd &Q, Eigen::MatrixXd &R) {int m = A.rows();int n = A.cols();Q = Eigen::MatrixXd::Identity(m, m);R = A;for (int k = 0; k < n; ++k) {Eigen::VectorXd x = R.block(k, k, m - k, 1);Eigen::VectorXd e1 = Eigen::VectorXd::Zero(m - k);e1(0) = 1;Eigen::VectorXd v = x - x.norm() * e1;v /= v.norm();Eigen::MatrixXd H = Eigen::MatrixXd::Identity(m, m);H.block(k, k, m - k, m - k) -= 2.0 * v * v.transpose();R = H * R;Q = Q * H.transpose();}
}
int main() {Eigen::MatrixXd A(3, 3); // 创建一个3x3的示例矩阵// 填充矩阵AA << 12, -51, 4,6, 167, -68,-4, 24, -41;Eigen::MatrixXd Q, R;householderQR(A, Q, R);std::cout << "矩阵 Q:\n" << Q << "\n\n";std::cout << "矩阵 R:\n" << R << "\n\n";Eigen::MatrixXd reconstructed_A = Q * R;std::cout << "重构的矩阵 A:\n" << reconstructed_A << "\n\n";return 0;
}
这篇关于Householder变换进行QR分解及其代码实现(C++)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




