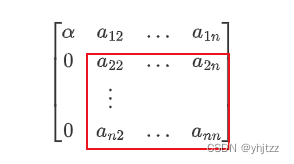
householder专题
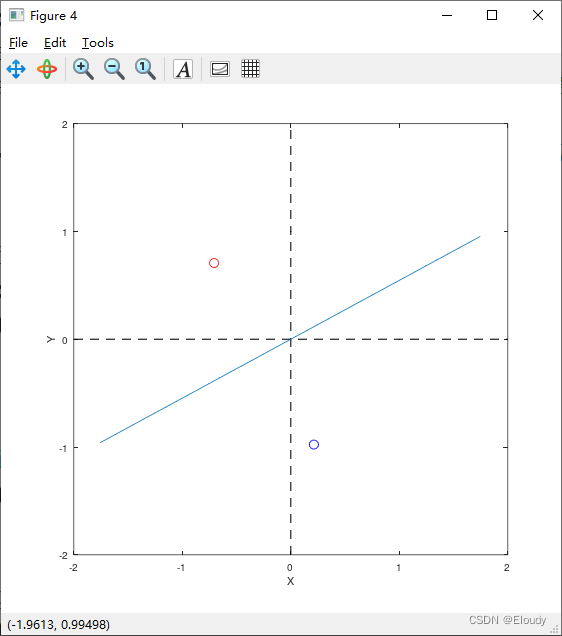
低维度向量的 Householder 反射变换 matlab 图示
1, 算法原理 设th 是一个弧度值, 令 Q = | cos(th) sin(th) | | sin(th) -cos(th) | S = span{ | cos(th/2.0) | } | sin(th/2.0) | x = (x1, x2) 是一个平面上的二维向量 计算 y = Q'x = Qx 则
【数值计算方法(黄明游)】矩阵特征值与特征向量的计算(五):Householder方法【理论到程序】
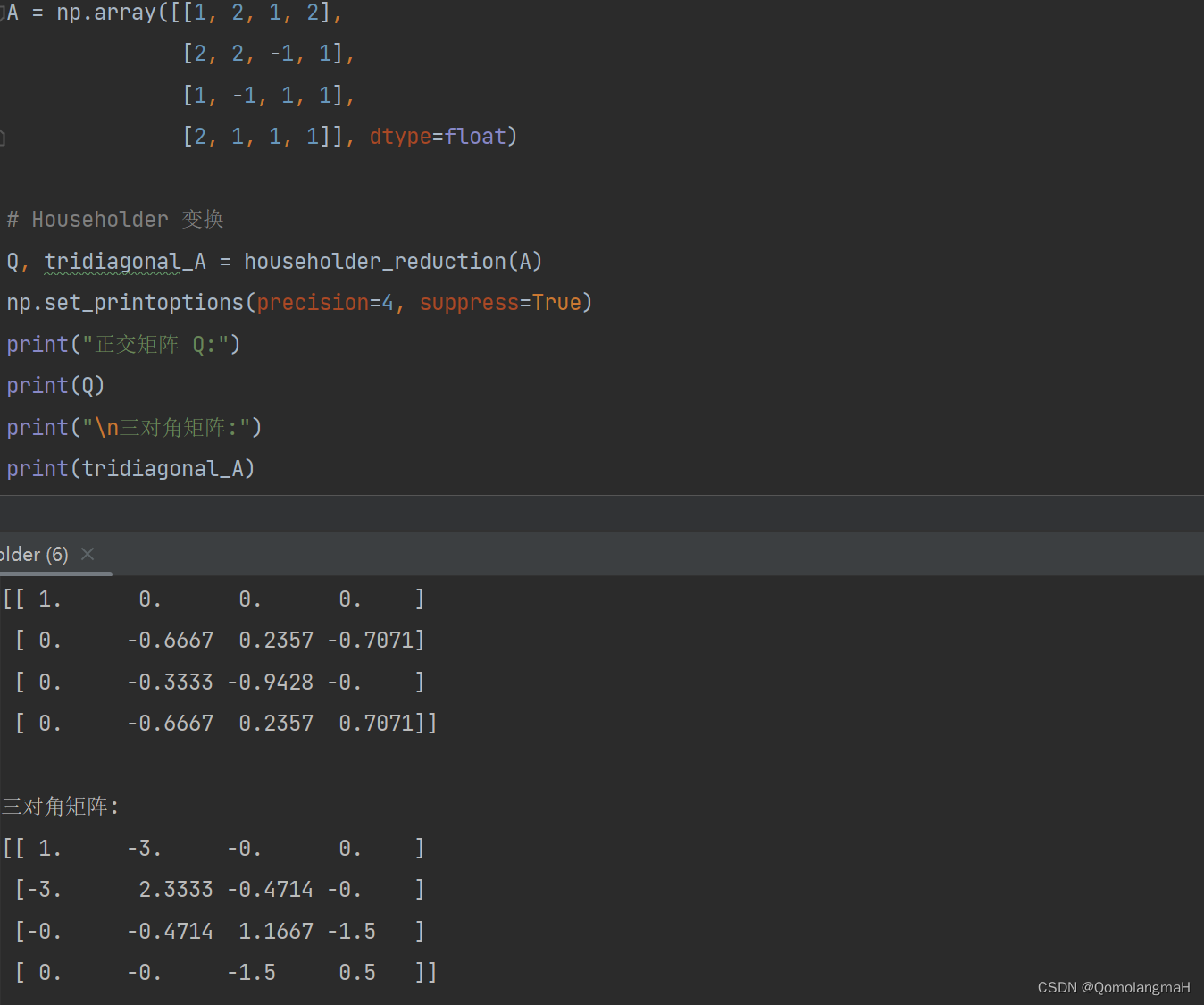
文章目录 一、Jacobi 旋转法二、Jacobi 过关法三、Householder 方法1. 旋转变换a. 旋转变换的选择b. 旋转变换的顺序 2. Householder矩阵(Householder Matrix)a. H矩阵的定义b. H变换的几何解释c. H变换的应用场景 3. H变换过程详解a. 过程介绍b. 细节解析 4. H变换例题解析 四、Python实现调试过程
householder进行矩阵QR分解
文章目录 1. Householder 进行QR分解 1. Householder 进行QR分解 A = Q R (1) A=QR\tag1 A=QR(1) A = [ 1 2 0 1 1 0 3 1 1 0 3 2 1 2 0 2 ] (2) A=\begin{bmatrix}1&2&0&1\\\\1&0&3&1\\\\1&0&3&2\\\\1&2&0&2\end{bmat
Givens旋转与Householder反射
参考 wiki https://www.wanweibaike.com/wiki-豪斯霍尔德变换 如何理解Householder变换和Givens旋转? - 荆哲的回答 - 知乎https://www.zhihu.com/question/51432776/answer/125819331 Givens旋转矩阵 Gii = cosθ,Gjj = cosθ,Gij = sinθ,Gji =
[矩阵的QR分解系列三] 豪斯霍尔德(Householder)变换
豪斯霍尔德变换 简介镜像变换反射变换镜像变换 性质基本性质目标方向旋转*初等反射矩阵* 转 *初等旋转矩阵* 例子引用 之前介绍的矩阵的三角分解系列介绍了利用矩阵初等变换解决了矩阵三角化问题以及具体的三角分解。但是以初等变换工具的三角分解方法并不能消除病态线性方程组不稳定问题,而且有时候对于可逆矩阵有可能也不存在三角分解。所以后面为了解决这里问题,发展出来了以正交(酉)变换的矩阵的
Householder变换进行QR分解及其代码实现(C++)
文章目录 简介前置理论Householder进行QR分解代码实现 简介 初等变换工具如三角分解(LU分解)可以用于求解线性方程组,但确实存在一些限制。例如,对于病态(ill-conditioned)的线性方程组,LU分解可能会导致数值不稳定的结果。此外,对于不可逆矩阵,LU分解也不适用。 为了克服这些问题,引入了QR分解,其中矩阵分解为正交矩阵Q和上三角矩阵R。QR分解对于任何


![[矩阵的QR分解系列三] 豪斯霍尔德(Householder)变换](https://img-blog.csdnimg.cn/20201205172854698.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2hvbnluaXU=,size_16,color_FFFFFF,t_70)