本文主要是介绍动态规划问题——骑士救公主,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题目:
给定一个二维数组map,含义是一张地图,如:
-2 -3 3
-5 -10 1
0 30 -5
骑士从左上角出发,每次只能向右或向下走,最后到达右下角见到公主。如果数字数负数,则骑士损失对应血量,如果是正数,骑士恢复对应血量,在任何位置骑士的血量都不能少于1,为了保证骑士能见到公主,初始血量至少是多少?根据map,返回初始血量。
思路:
定义和地图大小一样的矩阵 dp,dp[i][j] 的含义是如果骑士要走上位置(i,j),并且从该位置选一条最优的路径,最后走到右下角,骑士起码应该具备的血量。最终要的是dp[0][0]的结果。
代码实现:
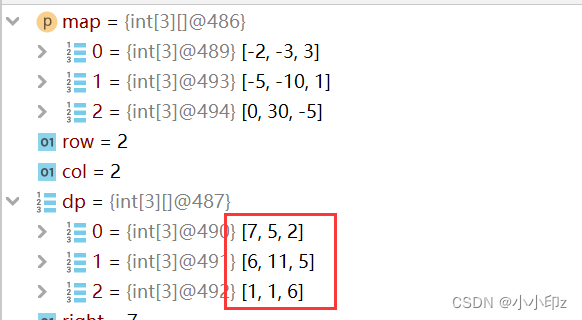
public static int minHP(int[][] map) {if (map == null || map.length == 0 || map[0] == null || map[0].length == 0) {return 1;}//初始化矩阵 dpint row = map.length;int col = map[0].length;int[][] dp = new int[row--][col--];//初始化dp矩阵右下角的值 如果这个位置是正数,有一滴血就可以,如果是负数,需要 绝对值+1dp[row][col] = map[row][col] > 0 ? 1 : -map[row][col] + 1;//初始化最下面一行 该位置值是 他右边值减去map中该位置的值,结果不能为负for (int j = col - 1; j >= 0; j--) {dp[row][j] = Math.max(dp[row][j+1] - map[row][j], 1);}int right = 0;int down = 0;for (int i = row -1; i >=0; i--) {//初始化最后一列dp[i][col] = Math.max(dp[i+1][col] - map[i][col], 1);//填其他位置for (int j = col - 1; j >= 0; j--) {right = Math.max(dp[i][j+1] - map[i][j], 1);down = Math.max(dp[i+1][j] - map[i][j], 1);dp[i][j] = Math.min(right, down);}}return dp[0][0];}测试结果:
这篇关于动态规划问题——骑士救公主的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









