本文主要是介绍【论文阅读】Graph Contrastive Learning with Adaptive Augmentation,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Graph Contrastive Learning with Adaptive Augmentation
用于图数据增强的图对比学习
文章目录
- Graph Contrastive Learning with Adaptive Augmentation
- 用于图数据增强的图对比学习
- 摘要
- 1 引言
- 二、模型方法
- 1.准备工作
- 2.对比学习框架
- 3.自适应图增强
- 3.1 拓扑级别的增强
- 3.2 节点属性级增强
- 4.实验
- 4.1 实验设置
- 4.2 RQ1:在节点分类上的性能
- 4.3 RQ2:消融研究
- 4.4 RQ3:灵敏度分析
- 5. 总结
摘要
近年来,对比学习(Contrastive Learning,CL)已成为一种成功的无监督图表示学习方法。大多数图的CL方法首先对输入图进行随机增强,以获得两个图的视图,并最大化两个视图表示的一致性。尽管图CL方法得到了繁荣的发展,但CL中的一个关键组成部分——图增强方案的设计,仍然很少被探索。我们认为,数据增强方案应该保留图的内在结构和属性,这将迫使模型学习对不重要的节点和边缘的扰动不敏感的表示。然而,现有的方法大多采用统一的数据增强方案,如统一降边和统一变换特征,导致性能次优。在本文中,我们提出了一种新的具有自适应增强的图对比表示学习方法,该方法包含了图的拓扑和语义方面的各种先验。具体来说,在拓扑层面上,我们设计了基于节点中心性度量的增强方案来突出重要的连接结构。在节点属性级别上,我们通过向不重要的节点特征添加更多的噪声来破坏节点特征,以强制模型识别底层的语义信息。我们在各种真实世界的数据集上进行了广泛的节点分类实验。实验结果表明,我们提出的方法始终优于现有的先进基线,甚至超过一些监督的方法,这验证了所提出的自适应增强对比框架的有效性。
1 引言
图表示学习主要用于分析图结构的数据。通常利用图神经网络(Graph Neural Networks,GNN)进行图表示学习,其目的是将节点转换为低维密集嵌入,以保留图的属性和结构特征。现有GNN模型多以监督的方式建立,需要大量的标记节点进行训练。对比学习是通过对比正样本对和负样本对,寻求最大化输入(即图像)与其表示(即图像嵌入)之间的相互信息(Mutual Information,MI)。
CL中的一个关键组成部分是图增强方法。现有的图增强方法有两个缺点:
- 在结构域或属性域中进行简单的数据增强不足以生成不同的邻域(上下文),特别是当节点特征稀疏时,导致难以优化对比目标。
- 以往的工作忽略了在进行数据扩充时节点和边缘影响的差异。eg.如果我们通过均匀地删除边来构造视图,去除一些有影响的边会降低嵌入质量。
对比目标学习到的表示对数据增强方案引起的破坏往往是不变的,因此数据增强策略应该自适应输入图,以反映其内在模式。该方案能够指导模型忽略在不重要的边缘上引入的噪声,从而学习输入图下的重要模式。 eg. 以除边方案为例,当随机去除边时,我们可以给不重要边的大概率,给重要边的小概率。
本文提出了一种新的无监督图表示学习的对比框架——具有自适应增强的图对比学习(Graph Contrastive learning with Adaptive augmentation,GCA),如下图所示:

图1:我们提出的深度图对比表示学习与自适应增强(GCA)模型。我们首先通过自适应图的结构和属性的随机增强来生成两个图的视图。然后,将这两个图输入一个共享的图神经网络(GNN)来学习表示。我们用一个对比目标来训练模型,它将一个节点的表示拉在一起,同时将节点表示远离两个视图中的其他节点表示。注意,我们将负样本定义为两个视图中的所有其他节点。因此,阴性样本来自两个来源,即视图内节点(紫色)和视图间节点(红色)。
在GCA中,我们首先通过自适应图的结构和属性的随机增强来生成两个图的视图。然后,我们使用对比损失来训练模型,以最大化这两个视图中节点嵌入之间的一致性。
具体地说,我们提出了一种在拓扑和节点属性级别上的联合自适应数据增强方案,即去除边缘和掩蔽特征,为不同视图中的节点提供不同的上下文,从而促进对比目标的优化。
此外,我们通过中心性度量来识别重要的边缘和特征维度。
然后,在拓扑层次上,我们通过给不重要的边自适应的去除概率,以突出重要的连接结构。在节点属性级别上,我们通过向不重要的特征维度添加更多的噪声来破坏属性,以强制模型识别底层的语义信息。
本文的核心贡献是两个方面:
- 提出了一个具有自适应增强的图对比表示学习方法。在自适应图结构和属性的拓扑结构和属性级别上共同执行数据增强,这鼓励了模型从这两个方面学习重要的特征。
- 在5个公共基准数据集下对节点分类进行了全面的实证研究,GCA始终优于现有的方法。
二、模型方法
1.准备工作

2.对比学习框架
模型寻求最大限度地提高不同视图之间的表示一致性。
①首先通过对输入执行随机图增强来生成两个图视图。
②采用了一个对比目标,强制每个节点在两个不同视图中的编码嵌入彼此一致,并可以与其他节点的嵌入区分开来。
方法:对于任意节点𝑣𝑖,其在一个视图𝒖𝑖中生成的嵌入都被视为锚点(命名标记),其在另一个视图𝒗𝑖中生成的嵌入形成正样本,而两个视图中的其他嵌入自然被视为负样本。
将每个正样本对(𝒖𝑖,𝒗𝑖)的目标函数定义为:
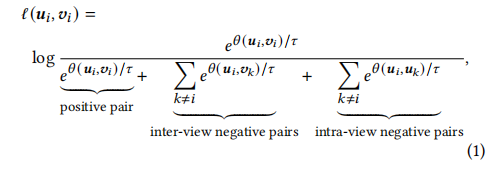
公式说明:给定一个正样本对,我们自然地将负样本定义为两个视图中的所有其他节点。因此,负样本来自两个来源,即视图间节点和视图内节点,分别对应于等式中分母中的第二项和第三项。由于两个视图是对称的,因此另一个视图的损失同样被定义为ℓ(𝒗𝑖,𝒖𝑖)。
总体目标函数定义为所有正样本对的平均值,即:
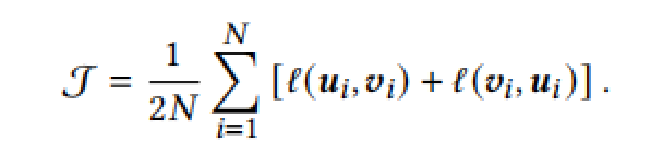
GCA训练算法如下:

算法说明:第1步,第2步对两个随机增广函数t ~ t和t’ ~ t进行抽样;通过对G执行破坏,生成两个图视图S1 = t(G)和G2 = t’(G);利用编码器f获得G1的节点嵌入量U;利用编码器f获得g2的节点嵌入量V;利用Eq.(2)计算对比目标J;采用随机梯度上升方法更新参数,使J最大化
3.自适应图增强
想法:在GCA模型中,我们建议设计增强方案,以倾向于保持重要的结构和属性不变,同时干扰可能不重要的链接和特征。
具体做法:通过随机移除边和掩蔽节点来破坏输入图中的特征,以及去除或掩盖的概率对于不重要的边或特征较高,对于重要的边或特征较低。
目的:更强调重要的结构和属性,而不是随机损坏的视图,这将指导模型保持基本的拓扑和语义图模式。
3.1 拓扑级别的增强
对于拓扑级增强,我们考虑一种破坏输入图的直接方法,其中我们随机删除图中的边。形式上,我们从原始E中抽样一个修改的子集 E ~ \widetilde{E} E 的概率为:
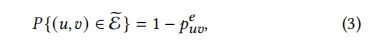
公式说明:(𝑢,𝑣)∈E, 𝑝 u v e 𝑝^{e}_{uv} puve是去除边(𝑢,𝑣)的概率,反应边的重要性; E ~ \widetilde{E} E 作为生成的视图中的边集。
节点中心性是一种广泛使用的度量方法,它量化了图中节点的影响。 基于边(𝑢,𝑣)中两个节点u,v的节点中心度定义为 w u v e w^{e}_{uv} wuve。给定一个节点中心性度量方法 φ c \varphi _{c} φc(·) : V :V :V→ R + R^{+} R+,定义边中心度为两个相邻节点中心度的平均值 w u v e = ( φ c ( u ) + φ c ( v ) ) / 2 w^{e}_{uv}=(\varphi _{c}(u) + \varphi_{c}(v))/2 wuve=(φc(u)+φc(v))/2。在有向图上边的重要性由它的指向节点表征,故只使用尾部节点的中心度 w u v e = φ c ( v ) w^{e}_{uv}=\varphi_{c}(v) wuve=φc(v)。
接下来,我们根据每条边的中心度来计算边的概率。因为边中心度可能受到数量级的影响,通过设置 s u v e = l o g w u v e s^{e}_{uv}=logw^{e}_{uv} suve=logwuve来减轻具有高度密集连接的节点的影响。然后将值转换为概率的归一化步骤之后获得概率,该归一化步骤定义为:

公式说明:其中 𝑝 𝑒 𝑝_{𝑒} pe作为超参控制全局去除边的概率, s m a x e s^{e}_{max} smaxe和 μ s e \mu ^{e}_{s} μse 分别是 s u v e s^{e}_{uv} suve的最大值和平均值,而 𝑝 τ < 1 𝑝_{\tau }<1 pτ<1代表截断概率,避免因为极高的去除概率将导致过度损坏的图结构。
对于节点中心度函数的选择,本文使用中心度、特征向量中心度和PageRank中心度这三个度量方法。
-
中心度。节点度本身可以是一个中心度量。在有向网络上使用入度,因为有向图中的一个节点的影响主要是由指向的节点所赋予的。优点:最简单、有效。缺点:所有相邻节点对该节点的重要性相同。
例如,在引文网络中,节点代表论文,边缘代表引文关系,度最高的节点很可能对应于有影响力的论文。 -
特征向量中心度。一个节点的特征向量中心度计算为其对应邻接矩阵的最大特征值的特征向量。优点:连接到多个相邻节点或连接到有影响的节点的节点将具有较高的特征向量中心度。
-
PageRank中心度。PageRank中心度定义为由PageRank算法计算的PageRank权重。优点:该算法沿有向边传播影响,将受影响量最大的节点视为重要节点。
三种方法的边中心度可视化:

数据集:空手道俱乐部数据集,分别包含由两名教练领导的两组学生。
虽然三种方案表现出细微的差异,但所有的增强方案都倾向于强调连接两组内两个教练(橙色)的边缘,而较少关注组间外围节点之间的连接。这验证了所提出的基于节点中心性的自适应拓扑增强方案可以识别图的基本结构。
3.2 节点属性级增强
在节点属性级别上,通过在节点特征中使用零随机遮蔽部分维度来向节点属性添加噪声。
形式上,我们首先抽样一个随机向量 𝒎 ~ ∈ 0 , 1 𝐹 \widetilde{𝒎}∈{0,1}^{𝐹} m ∈0,1F,其中它的每个维度都独立地从伯努利分布中抽取。
计算生成的节点特征 𝑿 ~ \widetilde{𝑿} X = [ x 1 ∘ m ~ ; x 2 ∘ m ~ ; . . . ; x N ∘ m ~ ] T [x_{1} \circ \widetilde{m} ; x_{2} \circ \widetilde{m}; ...; x_{N} \circ \widetilde{m}]^{T} [x1∘m ;x2∘m ;...;xN∘m ]T。
其中,[ ; ]是连接操作, ∘ \circ ∘是element-wise乘法,每个元素对应相乘。
概率 𝑝 𝑖 𝑓 𝑝^{𝑓}_{𝑖} pif反映节点特征第𝑖维的重要性。假设经常出现在有影响的节点中的特征维度应该是重要的,并定义特征维度的权重如下。
对于稀疏的 One-hot 节点特征,即对于任何节点𝑢和特征维度𝑖有 x u 𝑖 x_{u𝑖} xui∈{0,1},计算维度𝑖的权重为:
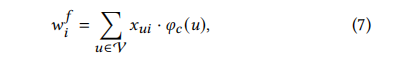
公式说明:其中, φ c ( ⋅ ) \varphi _{c}(·) φc(⋅)是一个用于量化节点重要性的节点中性度函数。 x u 𝑖 x_{u𝑖} xui∈{0,1}表示维度 i 在节点 u 中的出现情况, φ c ( u ) \varphi _{c}(u) φc(u)表示每次出现的节点的重要性。
举例,考虑一个引文网络,其中每个特征维度都对应于一个关键字。那么经常出现在一篇非常有影响力的论文中的关键词应该被认为是重要的并且带有启示性的信息。
对于密集、连续的节点 u 的节点特征 x u x_{u} xu,其中 x u 𝑖 x_{u𝑖} xui表示维数𝑖处的特征值,我们不能直接计算每个 One-hot 编码的出现次数。然后,我们用节点𝑢的绝对值| x u 𝑖 x_{u𝑖} xui|来测量维𝑖的特征值的大小:
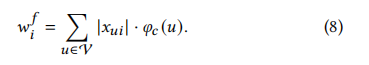
对权值进行归一化,以获得表示特征重要性的概率:
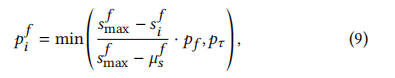
公式说明:其中 s 𝑖 𝑓 s^{𝑓}_{𝑖} sif = log w i f w^{f}_{i} wif , s m a x f s^{f}_{max} smaxf和 μ s f \mu ^{f}_{s} μsf 分别是 s i f s^{f}_{i} sif的最大值和平均值, p f p_{f} pf 代表全局节点特征的遮掩概率。
我们通过联合执行拓扑级和节点属性级的增强来生成两个被损坏的图视图 G 1 ~ \widetilde{G_{1}} G1 , G 2 ~ \widetilde{G_{2}} G2 。在GCA中,两个视图的概率 p e p_{e} pe 和 p f p_{f} pf 是不同的,其中第一个和第二个视图的概率分别用 p e , 1 p_{e,1} pe,1、 p f , 1 p_{f,1} pf,1和 p e , 2 p_{e,2} pe,2、 p f , 2 p_{f,2} pf,2表示。
在本文中,我们提出并评估了三个模型变量,分别表示为GCA-DE、GCA-EV和GCA-PR。请注意,所有的中心性和权重度量都只依赖于原始图的拓扑结构和节点属性。因此,它们只需要计算一次,并且不会带来太多的计算负担。
4.实验
在本节中,我们将通过回答以下问题来进行实验来评估我们的模型。
• RQ1.我们提出的GCA在节点分类方面是否优于现有的基线方法?
• RQ2.所有提出的自适应图增强方案都有利于模型的学习?每个图的增强方案是如何影响模型的性能?
• RQ3.所提出的模型对超参数敏感吗?关键超参数如何影响模型的性能?
我们首先简要介绍了实验设置,然后我们继续介绍实验结果及其分析的细节。
4.1 实验设置
1.数据集。5个被广泛使用的数据集:Wiki-CS、Amazon-Computers、Amazon-Photo、 Coauthor-CS 、Coauthor-Physics。
其中,Wiki-CS具有密集的数值特征,而其他四个数据集只包含稀疏的 One-hot 特征。对于Wiki-CS数据集,我们在其附带的公共分割上评估模型。对于其他四个数据集,由于它们没有可用的公共分割,我们改为随机分割数据集,其中分别选择10%、10%和其余80%的节点用于训练、验证和测试集。
2.评价方案。对于每个实验,我们都遵循维利科维奇介绍的线性评估方案,其中每个模型首先以无监督的方式进行训练;然后,利用得到的嵌入来训练和测试一个简单的ℓ2正则化逻辑回归分类器。我们对不同的数据分割进行20次运行,并报告每个数据集的平均性能,以进行公平评估。此外,我们在这些实验中以准确性来衡量性能。
3.Baseline。我们考虑代表性基线方法属于以下两类:(1)传统方法包括nede2[11]和(2)方法包括深度学习图自动编码器(GAE,VGAE)[22],深度图Infomax(DGI)[46],图形互信息最大化(GMI)[32],和多视图图表示学习(MVGRL)[16].此外,我们报告了使用逻辑回归分类器对原始节点特征和深度行走与嵌入连接到输入节点特征所获得的性能。为了直接比较我们提出的方法与监督的方法,我们还报告了两个代表性模型图卷积网络(GCN)[23]和图注意网络(GAT)[45]的性能,其中它们以端到端方式进行训练。对于所有的基线,我们将根据它们的官方实现来报告它们的性能。
4.2 RQ1:在节点分类上的性能

性能总结如表3所示。其中𝑿、𝑨、𝒀分别对应于节点特征、邻接矩阵和标签;无监督模型的最高性能以黑体突出显示;OOM表示在一个32GB的GPU上的内存不足。
总结:
(1)我们提出的模型在所有五个数据集上都显示出了强大的性能,始终优于无监督基线,验证了所提出的对比学习框架的优越性。
(2)在某些数据集(Wiki-CS)上,GAE 的性能比 DeepWalk+feature 更差,这归因于它们选择负样本的简单方法,即简单地基于边缘选择对比对。这一事实进一步证明了基于增强图视图在对比表示学习选择负样本的重要作用。
(3)MVGRL使用扩散来将全局信息合并到增强的视图中,但它仍然没有自适应地考虑不同的边对输入图的影响。实验结果验证了我们提出的自适应数据增强方案能够通过在扰动时保留重要的信息来提高嵌入质量。
4.3 RQ2:消融研究
GCA-T-A 表示具有统一拓扑和节点属性增强方案的模型,其中所有节点的丢弃边和掩蔽特征的概率被重置为相同的。变种 GCA-T 和 GCA-A 的定义类似,所有的变种都使用了中心度方法。

结论:拓扑级和节点属性级自适应增强方案在所有数据集上都一致地提高了模型性能。
4.4 RQ3:灵敏度分析

具有不同超参数的GCA对Amazon-Photo数据集在节点分类精度上的性能
设置 p e = p e , 1 = p e , 2 p_{e}=p_{e,1}=p_{e,2} pe=pe,1=pe,2, p f = p f , 1 = p f , 2 p_{f}=p_{f,1}=p_{f,2} pf=pf,1=pf,2。
结论:从图中可以看出,当参数不太大时,节点分类的精度性能相对稳定,如图中的平台所示。因此,我们得出结论,总的来说,我们的模型对这些概率不敏感,证明了对超参数扰动的鲁棒性。如果概率设置得太大(例如,>0.5),原始图将被严重破坏。例如,当𝑝𝑒=0.9时,几乎所有现有的边都已被删除,从而导致生成的图视图中出现孤立的节点。在这种情况下,GNN很难从节点邻域学习有用的信息。因此,学习到的两个图视图中的节点嵌入不够独特,这将导致优化对比目标的困难。
5. 总结
在本文中,我们开发了一种新的具有自适应增强的图对比表示学习框架。我们的模型通过最大化由自适应图增强生成的视图之间的节点嵌入的一致性来学习表示。所提出的自适应增强方案首先通过网络中心性度量来识别重要的边缘和特征维度。然后,在拓扑层次上,我们通过在不重要的边缘上分配较大的概率来随机去除边缘,以强制模型识别网络连接模式。在节点属性级别上,我们通过向不重要的特征维度添加更多的噪声来破坏属性,以强调底层的语义信息。我们已经使用各种真实世界的数据集进行了全面的实验。实验结果表明,我们提出的GCA方法始终优于现有的最先进的方法,甚至超过了一些有监督的方法。
这篇关于【论文阅读】Graph Contrastive Learning with Adaptive Augmentation的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








![[论文笔记]LLM.int8(): 8-bit Matrix Multiplication for Transformers at Scale](https://img-blog.csdnimg.cn/img_convert/172ed0ed26123345e1773ba0e0505cb3.png)
