本文主要是介绍论文笔记:Piecewise classifier mappings: Learning FG learners for novel categories with few examples,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Piecewise classifier mappings: Learning fine-grained learners for novel categories with few examples
文章目录
- Piecewise classifier mappings: Learning fine-grained learners for novel categories with few examples
- 0 摘要
- 1 引言
- 2 相关工作
- 3 方法
- 3.1 学习策略、涉及到的符号
- 3.2 模型
- 特征表示
- 分类器映射
- 网络训练
- 不懂之处
- 4 实验
- 4.1 数据集、细节
- 4.2 结果
- 4.3 消融实验
- 分段映射vs全连接映射
- m ϕ t m_{\phi_{t}} mϕt的层数
- 5 结论
0 摘要
few-shot细粒度分类(FSFG,few-shot fine-grained recognition),用极少样本为新类别建立分类器。
本文提到的网络包括双线性特征学习模块和分类器映射模块。关键是后者分类模块的分段映射"piecewise mapping"函数,它学习一组更多可获得的子分类器来生成决策边界。以元学习的方式学习基于辅助数据集的**“示例-分类器”映射**。
1 引言
旨在从很少的带有标签的训练示例中学习细粒度分类器。
提出了一个端到端可训练网络,包括双线性特征学习模块(将少量样本的区别信息编码进特征向量)和分类器映射模块(学习一组更多可获得的子分类器来生成决策边界)。
高度非线性映射用子向量-子分类器映射来拟合,再将子分类器组合为全局分类器,区分不同类别的样本。基于隐式“部分”的特征到分类器映射可对简单和纯净的信息进行编码,使映射更容易。
piecewise mapping减少了模型参数量,计算效率更高。以元学习方式,使用辅助数据集学习示例-分类器映射。贡献:
- few-shot设置,提出了一种元学习策略来解决FSFG问题。
- 名为“piecewise mapping”的示例到分类器映射策略,用BCNN特征以参数很少的方式学习判别式分类器。
- 充分实验,性能优异
2 相关工作
细粒度分类
区别特征表示、对齐、[无]监督定位等。
通用few-shot图像识别
研究从几个示例中赋予学习系统快速学习新颖类别的能力的可能性。极端的one-shot learning。
learning-to-learn范式、匹配网络、原型网络、回归网络、元学习、与模型无关的元学习方案、训练新颖类别的参数预测器。
few-shot 细粒度图像识别更具挑战。分段映射组件。
3 方法
3.1 学习策略、涉及到的符号
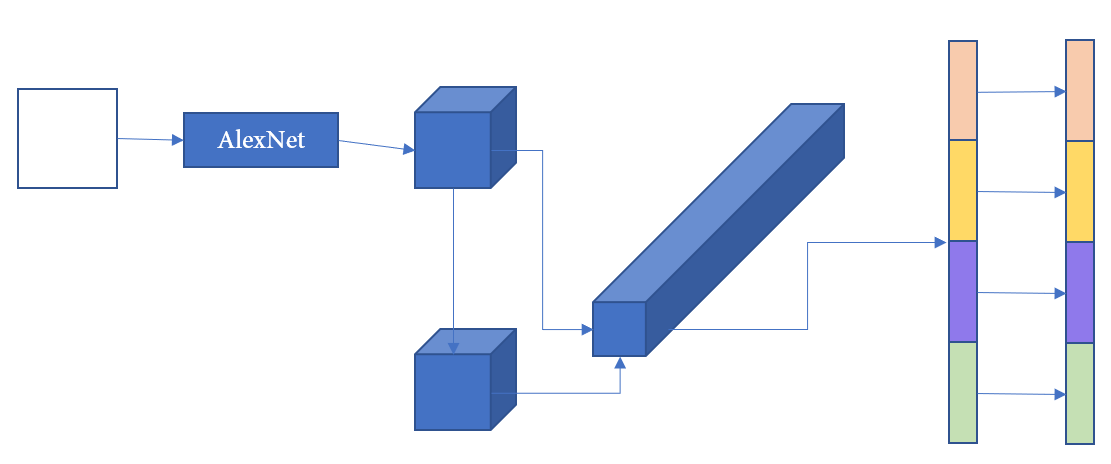
以元学习(meta-learning)框架为基础,将分类器生成过程看作是映射函数(从少数带有类别标签的训练示例到其相应类别分类器,不是类别,是分类器)。
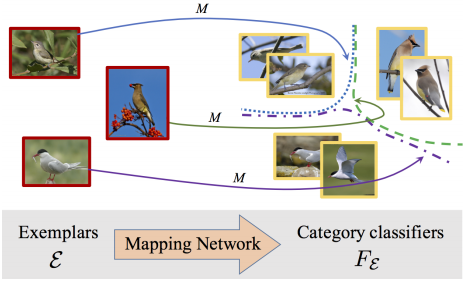
辅助训练集 B \mathcal B B包含 N N N个训练图像 B = { ( I 1 , y 1 ) , . . . , ( I N , y N ) } \mathcal B=\{(\mathcal{I_1},y_1),...,(\mathcal{I_N},y_N)\} B={(I1,y1),...,(IN,yN)}( I i \mathcal I_i Ii是示例图像, y 1 ∈ { 1 , 2 , . . . , C B } y_1\in\{1,2,...,C_\mathcal{B}\} y1∈{1,2,...,CB}是标签)。映射功能学习之后,应用于测试集 N \mathcal{N} N评估性能,注意, N \mathcal{N} N中存在 B \mathcal{B} B没有的类别(新类别)。
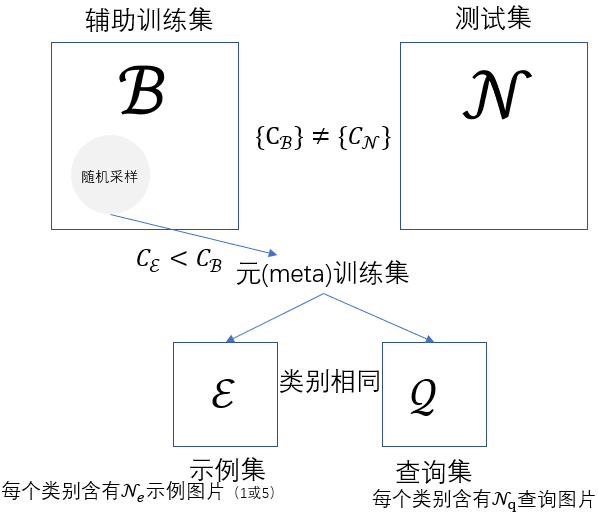
在训练过程中, E \mathcal{E} E将被输入到要学习的映射函数 M M M中,以生成类别分类器 F E F_{\mathcal{E}} FE, E → F E \mathcal{E}\to F_{\mathcal{E}} E→FE。 F E F_{\mathcal{E}} FE再应用于 Q \mathcal{Q} Q以评估分类损失(通过损失优化模型是通过查询集而不是示例集),通过最小化分类损失来学习映射功能。形式化表示: min λ E E , Q ∼ B { L ( F E ◦ Q ) } \min_λ E_{{\mathcal E,\mathcal Q}\sim \mathcal B}\{\mathcal L(F_\mathcal{E}◦\mathcal Q)\} minλEE,Q∼B{L(FE◦Q)}, λ \lambda λ表示映射函数 M M M的参数, L \mathcal L L是损失函数, F E ◦ Q F_\mathcal{E}◦\mathcal Q FE◦Q表示将示例集 E \mathcal E E生成的类别分类器 F E F_{\mathcal E} FE应用于查询集 Q \mathcal Q Q。
3.2 模型
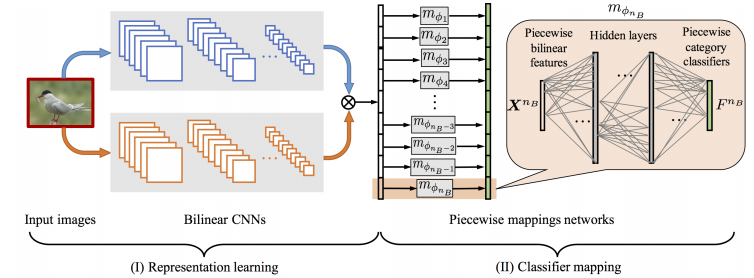
特征表示
使用BCNN(见论文《Bilinear CNN Models for Fine-grained Visual Recognition),特征图 f A ( I ) ∈ R n A × L f_A(\mathcal I)\in \mathbb R^{n_A\times L} fA(I)∈RnA×L和 f B ( I ) ∈ R n B × L f_B(\mathcal I)\in \mathbb R^{n_B\times L} fB(I)∈RnB×L的位置向量做向量外积生成特征图,再全局池化生成特征向量 x ∈ R D × 1 , D = n A × n B x\in\mathbb R^{D\times1},D=n_A\times n_B x∈RD×1,D=nA×nB。(BCNN论文里面是 f A T f B f_A^Tf_B fATfB,这篇论文是 f A f B T f_Af_B^T fAfBT,不过基本上差不多)
x x x看作是子向量 x t x^t xt的集合: x = [ x 1 ; x 2 ; . . . ; x t ; . . . ; x n B ] , ∀ t : x t ∈ R n A × 1 x=[x^1;x^2;...;x^t;...;x^{n_B}],\forall t:x^t\in \mathbb{R}^{n_A\times1} x=[x1;x2;...;xt;...;xnB],∀t:xt∈RnA×1, x t x^t xt是 f A f_A fA的 f B f_B fB的第 t t t个特征的调制特征,类似于注意力机制中的乘法特征交互。(把整个长向量看作 n B n_B nB个 n A n_A nA维短(段)向量)
为了表示一组属于类别 k k k的 N e N_e Ne样本图像,通过以下方式将平均图像表示形式计算为类别级别表示:
X k = 1 N e ∑ i = 1 N e x i X_k=\frac1{N_e}\sum_{i=1}^{N_e}x_i Xk=Ne1i=1∑Nexi
所有 x i x_i xi对应的 y i = k y_i=k yi=k。
分类器映射
该任务是将这些中间类别级别表示形式映射到其相应的类别分类器中。
通过映射 M M M计算每个类别的 D D D维分类器 F k ∈ R D F_k\in\mathbb R^D Fk∈RD,形式化表示: M : R D → R D M:\mathbb R^D\to\mathbb R^D M:RD→RD。
朴素方案:线性或非线性全连接映射(原文global mapping)eg, F K = W g X k + b g F_K=W_gX_k+b_g FK=WgXk+bg。缺点:拟合困难、参数爆炸
分段映射策略:双线性特征 X k X_k Xk可以看作是子向量 X k t X^t_k Xkt的集合,每个子向量都描述了对象的隐式“部分”。可以通过检查对象的每个“部分”是否与示例兼容来测试对象是否属于示例中描述的类别。
做法:将每个子向量 X t k X_t^k Xtk映射到其对应的子分类器 F k t F^t_k Fkt中,然后将子分类器组合在一起以生成全局类别分类器。
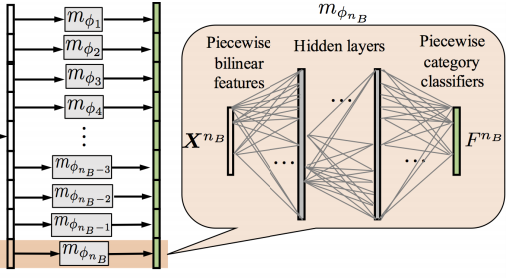
F k t = m ϕ t ( X k t ) F k = [ F k 1 ; F k 2 ; . . . ; F k n B ] F^t_k=m_{\phi_t}(X^t_k)\\ F_k=[F^1_k;F^2_k;...;F^{n_B}_k] Fkt=mϕt(Xkt)Fk=[Fk1;Fk2;...;FknB]
通过对全连接层分段,减少了参数量,容易训练。
这样理解:通过第一个短向量(描述头部)看是否是第一个类别,通过第二个短向量(表示翅膀)看是否是第二个类别……,整合所有结果得到最终预测。
网络训练
查询样本 x x x,类别标签 y = c y=c y=c,预测分布 p M ( y = c ∣ x ) = exp ( F c ⋅ x ) ∑ c ′ exp ( F c ′ ⋅ x ) p_M(y=c|x)=\frac{\exp(F_c\cdot x)}{\sum_{c'}\exp(F_{c'}\cdot x)} pM(y=c∣x)=∑c′exp(Fc′⋅x)exp(Fc⋅x),损失: J ( x , y ) = − log ( p M ( c ∣ x ) ) \mathcal{J}(x,y)=-\log(p_M(c|x)) J(x,y)=−log(pM(c∣x))。
- 从 B \mathcal B B中采样示例集 E \mathcal E E训练,训练得到分类器 F E F_{\mathcal E} FE。
- 建立查询集,通过最小化 J ( Q ) \mathcal{J(Q)} J(Q)进行优化。

E \mathcal E E用于建立分类器, Q \mathcal Q Q用于优化分类器。
不懂之处

- 从上面这句话和公式来说,类别数目应该和分类器数目相同,但是按照前面双线性那部分,有多少个分类器,每个分类器维数应该取决于主干网络得到特征图的通道数?
- 怎么从数据集 B \mathcal B B应用到数据集 N \mathcal N N上?可能存在新的类别,怎么保证兼容?
4 实验
4.1 数据集、细节
数据集:cub,dogs,cars。每个数据集分成两个部分 B , N \mathcal{B,N} B,N(不重叠)。
训练:将示例集 E \mathcal E E的类别大小设置为与测试集中 N \mathcal N N的类别数相同。 N e = 1 N_e=1 Ne=1( N e = 5 N_e=5 Ne=5)分别对应few-shot和five-shot, N q N_q Nq都设置为20。
测试: N \mathcal N N的每个类别随机选择1或5各示例。随机选择另外20个样本来评估识别性能。重复此评估过程20次,并将平均分类准确性用作评估标准。
AlexNet作为BCNN中的两个流。采用Places 205数据库预先训练AlexNet模型。
首先在辅助训练集上微调双线性特征学习模块,然后在分类器学习过程中冻结。映射函数为三层,其中每层采用1024个隐藏单元,激活函数为指数线性单元,SGD,学习率0.1。
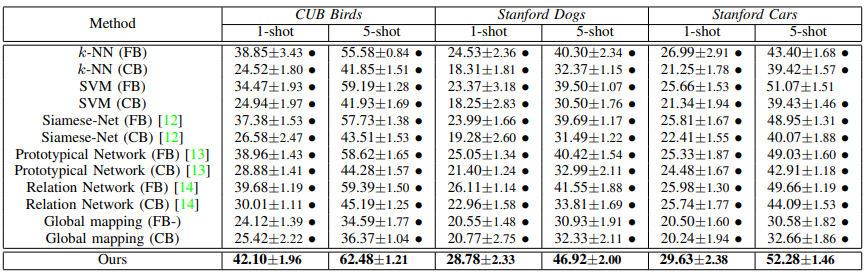
4.2 结果
4.3 消融实验
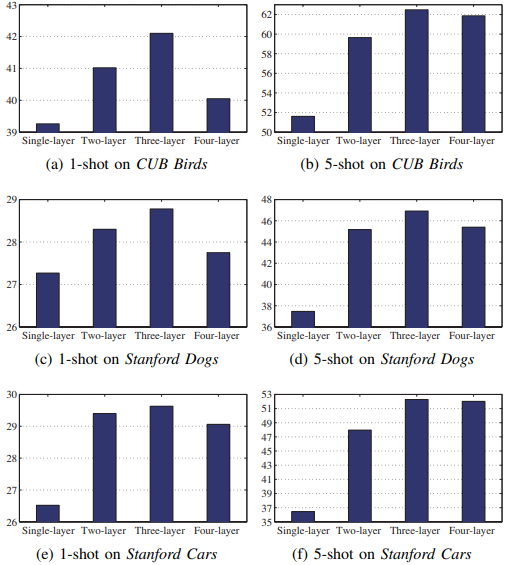
分段映射vs全连接映射

m ϕ t m_{\phi_{t}} mϕt的层数
5 结论
提出了端到端的可训练网络,受BCNN的启发,是为细粒度的few-shot learning量身定制。关键是分段分类器映射模块。
未来方向,使用迁移学习将数据集进行推广。
这篇关于论文笔记:Piecewise classifier mappings: Learning FG learners for novel categories with few examples的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







