https://cn.vjudge.net/problem/Gym-101991J
题目很长,其实就是给你一个正三角形,并且告诉你它的中点在Z轴上以及法向量,边长和顶点A的坐标(自由度已定),让你求A,B,C到Z轴上一点H的距离。
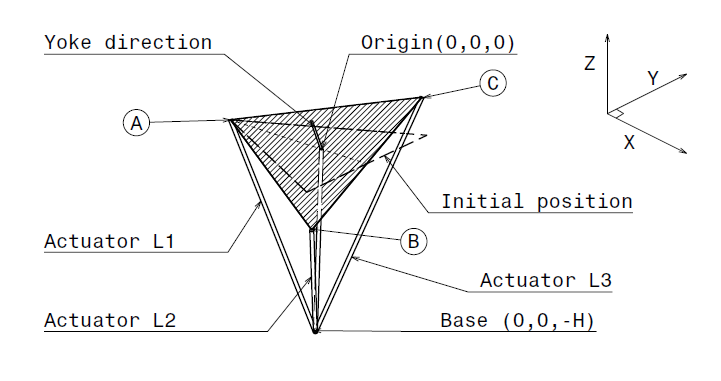
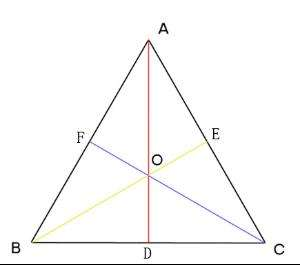
题解:高考向量题,考虑正三角形ABC,我们把OB拆成OD加DB,OD=-OA/2,DB可以通过连立三个方程得到(它垂直于AO和法向量,他的长度为L/2)
坑:
我一开始拆的是OA+AB,公式太长不可解orz,
后来解方程的时候写错了orz
然后y写成xorz
最后没考虑逆时针输出orz(这里要用叉积判一下,OA X OB 的方向要与法向量同)


#include<algorithm> #include<iostream> #include<stdlib.h> #include<string.h> #include<math.h> #include<stdio.h> #include<vector> #include<queue> #include<string> #include<ctime> #include<stack> #include<map> #include<set> #include<list> using namespace std; #define rep(i,j,k) for(int i = (int)j;i <= (int)k;i ++) #define per(i,j,k) for(int i = (int)j;i >= (int)k;i --) #define debug(x) cerr<<#x<<" = "<<(x)<<endl #define mmm(a,b) memset(a,b,sizeof(a)) #define pb push_back //#define x first //#define y second typedef double db; typedef long long ll; const int MAXN = 100010;; const int maxn = MAXN; struct V {db x, y,z;V() {}void sc() { scanf("%lf%lf", &x, &y); }V(db a, db b) : x(a), y(b) { }V operator+(V o) { return V(x + o.x, y + o.y); }V operator-(V o) { return V(x - o.x, y - o.y); }db L() { return sqrt(x * x + y * y); }V N() {db l = L();return V(x / l, y / l);}V rot(db th) { return V(x * cos(th) - y * sin(th), x * sin(th) + y * cos(th)); }V operator*(db z) { return V(x * z, y * z); }db operator*(V o) { return x * o.x + y * o.y; }db operator|(V o) { return x * o.y - o.x * y; }void pr() { printf("%lf %lf\n", x, y); } } p[maxn];//三维几何函数库#define eps 1e-8 #define zero(x) (((x)>0?(x):-(x))<eps) struct point3 { db x, y, z; }; struct line3 { point3 a, b; }; struct plane3 { point3 a, b, c; };//计算cross product U x V point3 xmult(point3 u, point3 v) {point3 ret;ret.x = u.y*v.z - v.y*u.z;ret.y = u.z*v.x - u.x*v.z;ret.z = u.x*v.y - u.y*v.x;return ret; }//计算dot product U . V db dmult(point3 u, point3 v) {return u.x*v.x + u.y*v.y + u.z*v.z; }//矢量差 U - V point3 subt(point3 u, point3 v) {point3 ret;ret.x = u.x - v.x;ret.y = u.y - v.y;ret.z = u.z - v.z;return ret; } point3 addt(point3 u, point3 v) {point3 ret;ret.x = u.x + v.x;ret.y = u.y + v.y;ret.z = u.z + v.z;return ret; }//取平面法向量 point3 pvec(plane3 s) {return xmult(subt(s.a, s.b), subt(s.b, s.c)); } point3 pvec(point3 s1, point3 s2, point3 s3) {return xmult(subt(s1, s2), subt(s2, s3)); }//两点距离,单参数取向量大小 db distance(point3 p1, point3 p2) {return sqrt((p1.x - p2.x)*(p1.x - p2.x) + (p1.y - p2.y)*(p1.y - p2.y) + (p1.z - p2.z)*(p1.z - p2.z)); }//向量大小 db vlen(point3 p) {return sqrt(p.x*p.x + p.y*p.y + p.z*p.z); }int main() {freopen("jupiter.in", "r", stdin);int t; cin >> t;while (t--) {point3 N, A;db l, h;scanf("%lf%lf%lf%lf%lf%lf%lf%lf", &N.x, &N.y, &N.z, &A.x, &A.y, &A.z, &l, &h);//scanf("%f%f%f%f%f%f%f%f", &N.x, &N.y, &N.z, &A.x, &A.y, &A.z, &l, &h);//cin >> N.x >> N.y >> N.z >> A.x >> A.y >> A.z >> l >> h;point3 H = { 0.,0.,-h };db La, Lb, Lc;db up = N.z*A.x - A.z*N.x;db under = N.y*A.x - A.y*N.x;db coy = -up / under;db cox =( N.z + N.y*coy)/(-N.x);cox = (A.z + A.y*coy) / (-A.x);db zz=l*l / 4.0/(coy*coy + cox*cox + 1.0) ;db z = l/sqrt(coy*coy + cox * cox + 1.0)/2.0;//db z = l / 2.0 / (coy + cox + 1.0);db x = cox * z;db y = coy * z;point3 b = { x,y,z };point3 c = { -x,-y,-z };point3 t = xmult(A, b);if (t.z*N.z > 0);else swap(b, c);point3 unA = { -A.x / 2.,-A.y / 2.,-A.z / 2. };point3 B = addt(unA, b);point3 C = addt(unA, c);La = distance(A, H);Lb = distance(B, H);Lc = distance(C, H);//if (N.z < 0)swap(Lb, Lc);printf("%.6lf %.6lf %.6lf\n", La,Lb,Lc);}//cin >> t; } /* 2 13 -18 1 7 5 -1 15 12 -12 -17 1 7 -5 -1 15 32 13 -18 1 7 5 -1 15 12 -12 -17 1 7 -5 -1 15 3 */
ps:第一次霸榜??
然后抄一个三维模板,
这个板子的话就厉害了 ,有了二维向量的一切操作。
这里的旋转操作,可以让向量V绕一个法向量n逆时针转theta度。
于是我们就只有两行代码了,
V3 B = N.rot(A, PI*2.0 / 3.0);
V3 C = N.rot(A, PI*4.0 / 3.0); #include<algorithm> #include<iostream> #include<stdlib.h> #include<string.h> #include<math.h> #include<stdio.h> #include<vector> #include<queue> #include<string> #include<ctime> #include<stack> #include<map> #include<set> #include<list> using namespace std; #define rep(i,j,k) for(int i = (int)j;i <= (int)k;i ++) #define per(i,j,k) for(int i = (int)j;i >= (int)k;i --) #define debug(x) cerr<<#x<<" = "<<(x)<<endl #define mmm(a,b) memset(a,b,sizeof(a)) #define pb push_back //#define x first //#define y second typedef double db; typedef long long ll; const int MAXN = 100010;; const int maxn = MAXN; const double eps = 1e-8; const double PI = acos(-1.0); struct V3 {db x, y, z;V3() {}V3(db xx, db yy, db zz) :x(xx), y(yy), z(zz) {}void sc() {scanf("%lf%lf%lf", &x, &y, &z);}db L() { return sqrt(x*x + y * y + z * z); }V3 N() { db l = L(); return V3(x / l, y / l, z / l); }V3 operator+(V3 o) { return V3(x + o.x, y + o.y,z+o.z); }V3 operator-(V3 o) { return V3(x - o.x, y - o.y,z-o.z); }V3 operator*(db zz) { return V3(x * zz, y * zz,z*zz); }db operator*(V3 o) { return x * o.x + y * o.y+z*o.z; }V3 operator|(V3 o) { return V3(y*o.z-z*o.y,z*o.x-x*o.z,x * o.y - o.x * y); } }; int sgn(db x) {if (fabs(x) < eps)return 0;else if (x > 0)return 1;else return -1; } struct L3 {V3 s, e;L3() {}L3(V3 ss, V3 ee) :s(ss), e(ee) {}V3 rot(V3 p, db arg) {if (sgn(((s - p) | (e - p)).L()) == 0)return p;V3 f1 = (e - s) | (p - s);V3 f2 = (e - s) | (f1);db len = ((s - p) | (e - p)).L() / (s - e).L(); f1 = f1.N()*len; f2 = f2.N() * len;V3 h = p + f2;V3 pp = h + f1;return h + ((p - h)*cos(arg)) + ((pp - h)*sin(arg));}};int main() {freopen("jupiter.in", "r", stdin);int t; cin >> t;while (t--) {V3 n, A;n.sc(); A.sc();db L, H;scanf("%lf%lf", &L, &H);L3 N = L3(V3(0, 0, 0), n);V3 base = V3(0, 0, -H);V3 B = N.rot(A, PI*2.0 / 3.0);V3 C = N.rot(A, PI*4.0 / 3.0);printf("%.6lf %.6lf %.6lf\n", (base - A).L(), (base - B).L(), (base - C).L());}//cin >>t; } /* 2 13 -18 1 7 5 -1 15 12 -12 -17 1 7 -5 -1 15 32 13 -18 1 7 5 -1 15 12 -12 -17 1 7 -5 -1 15 3 */





