【调度算法】NSGA II

本文主要是介绍【调度算法】NSGA II，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

简介

NSGA-II（Nondominated Sorting Genetic Algorithm II）是一种经典的多目标优化算法，由Srinivas和Deb于2000年在NSGA的基础上提出，用于解决多目标优化问题。相较于NSGA，NSGA-II在运行速度和解集的收敛性上表现更好，成为了其他多目标优化算法性能的基准。

以下是 NSGA-II 的基本步骤：

1. 初始化种群：首先，随机生成一个包含多个个体的初始种群。每个个体都代表一个潜在的解。

2. 计算适应度：对于每个个体，计算其在目标函数空间中的适应度。适应度的计算可以根据具体问题而定，一般使用评价指标（如距离、优劣等）来表示个体的优劣程度。

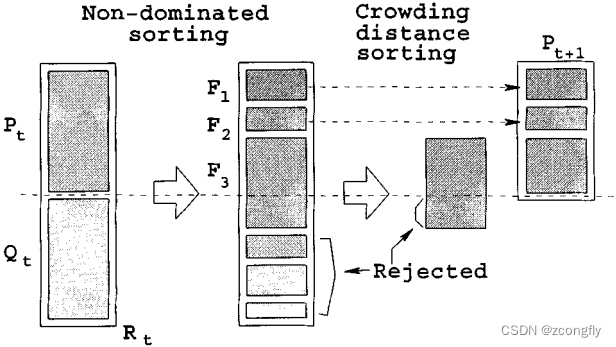
3. 非支配排序：NSGA-II 使用非支配排序技术，将种群中的个体划分为多个前沿。这个排序过程确定每个个体的非支配级别，以标识哪些个体占据 Pareto 前沿的不同位置。较高级别的个体不被较低级别的个体支配。

4. 拥挤距离计算：为了保持 Pareto 前沿的多样性，NSGA-II 计算拥挤距离，以度量个体在目标空间的密度。拥挤距离越大，个体之间的距离越远，从而有助于保持 Pareto 前沿上的均匀分布。

5. 选择操作：NSGA-II 使用二元锦标赛（binary tournament）作为选择操作，在每代中，首先使用二元锦标赛选择操作从当前种群中随机选择两个个体，然后选择其中具有更高非支配级别的个体。这个选择过程是通过比较个体的非支配级别和拥挤距离来执行的。

6. 交叉/变异操作：将选择出的个体通过交叉（crossover）和变异（mutation）操作生成父代种群。将父代和子代合并成一个更大的候选种群。

7. 迭代：将候选种群重新进行非支配排序、拥挤距离计算、选择、交叉、变异，生成新的子代种群，迭代执行，直到满足停止条件（如达到最大迭代次数或收敛到满意的 Pareto 前沿解）。

GA→NSGA II

NSGA II是从NSGA改进过来的，个人感觉NSGA相对传统的GA算法改进不多，故这里直接梳理一下NSGA II相对传统的GA作了哪些改进。

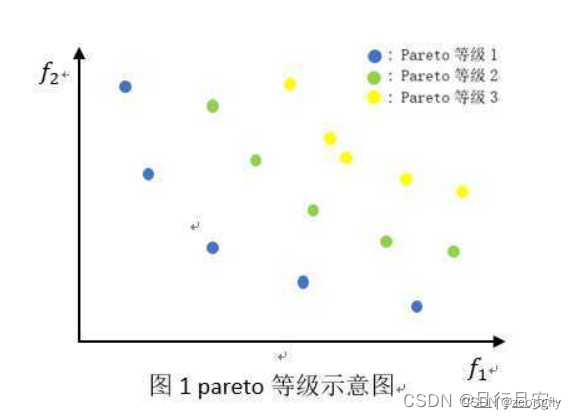
1. 非支配解和非支配排序：NSGA-II 引入了非支配排序，它通过将个体划分为多个前沿来确定每个个体的非支配级别。这种排序方法有助于找到 Pareto 前沿上的多样性解，而传统 GA 通常只关注单一的目标。

关于支配与非支配的概念，可以看这篇文章：https://blog.csdn.net/weixin_43893771/article/details/106689335

简单说，在多目标优化问题中，如果对于所有的目标，解1都优于解2，就称解1“支配于”解2；若解1在一部分目标上的表现优于解2，在另一部分的目标上的表现劣于解2，则称解1和解2之间互不支配（非支配）。非支配解之间由于其在不同目标上表现各有优劣，势均力敌，可将它们放在同一层级，称为“ Pareto 前沿层”，各层之间存在明显的上层支配下层的关系，因而我们可以对这些层次之间进行排序，规定表现最优的解在第一层，支配于下边的所有解，依次类推（类比一下人与人之间的三六九等）。这样，就对多目标问题的目标函数和解的评价建立了一个很好的描述模型。在下边的二维视图中可以明显地看出解的支配与非支配关系。

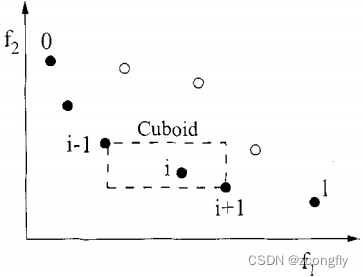
2. 拥挤距离：NSGA-II 引入了拥挤距离来维护 Pareto 前沿上解的多样性。拥挤距离度量了个体在目标空间的密度，有助于确保前沿上的解均匀分布。

直观上理解，某个解的拥挤距离可认为是以该解所在的Pareto 前沿层的左右两边的相邻两个解（以二维为例）为顶点构成的长方形的周长（极端的两个端点拥挤距离设为一个较大值）。扩展到高维，在计算拥挤距离时，个体通常被分配到一个多维空间中的一个长方形（或超立方体）中，这个长方形的边长由个体在每个维度上的分布情况决定。拥挤距离是由各个维度上的间隔之和组成，通常用于保持前沿上的解的分散性，使算法能够在多个目标函数下找到更多高质量的解。

3. 精英策略：将父代和子代连接成一个2N的种群是NSGA II中的一种实现精英主义的策略。在下一代中，最优解通常是当前种群中的一部分。通过将父代和子代合并成一个更大的种群，最优解不容易在选择操作中被遗漏。另外，子代通常包含一些新的解决方案，而父代包含了遗传信息，合并子代和父代也有助于保持种群的多样性。

注：实际上，我们还可以连接多代（如父代、子代和孙代）形成一个更大的种群（3N或更多），这被称为多代连接。

4. 二元锦标赛选择：传统的GA通常用的是轮盘赌选择，NSGA II中使用的是二元锦标赛选择（实际上，两者都是特别简单的算法，其选用可以参考我的另一篇文章：【调度算法】关于轮盘赌和锦标赛两种选择算子的选用思考），确切地说，它是通过二元锦标赛和拥挤距离，共同完成对下一代的选择。

原文(A Fast and Elitist Multiobjective Genetic Algorithm:NSGA-II)摘录：
It is important to note that we use a binary tournament selection operator but the selection criterion is now based on the crowded-comparison operator ${\prec }_n$.

用大白话说就是，选择子代种群时，使用二元锦标赛选择算法，并且在进行二元锦标赛时，选择标准是基于拥挤距离来确定获胜者。即，拥挤距离用于衡量解的拥挤程度，以确定哪个解应该在二元锦标赛中获胜。

算法实现

原代码GitHub地址：https://github.com/haris989/NSGA-II/tree/master
应该是最早最简单的对NSGA II的复现吧（膜拜大佬）。只是对原算法添加了注释，基本没有对主要函数进行修改。

# Importing required modules
import math
import random
import matplotlib.pyplot as plt# First function to optimize
def function1(x):value = -x ** 2return value# Second function to optimize
def function2(x):value = -(x - 2) ** 2return value# Function to find index of list
def index_of(a, list):'''在给定的列表中查找指定元素的索引:param a: 要查找的元素:param list: 要查找的列表:return: 元素a在list中的索引'''for i in range(0, len(list)):if list[i] == a:return ireturn -1# Function to sort by values
def sort_by_values(list1, values):'''根据给定的值列表对另一个列表进行排序，并返回排好序后的索引列表.:param list1: 要排序的列表:param values: 用于排序的值列表:return: 排序后的列表，返回的是索引？？？'''sorted_list = []while len(sorted_list) != len(list1):if index_of(min(values), values) in list1:  # 判断values中最小值的索引是否为list1中的元素（？？？为毛？？？这样会陷入死循环吧？）sorted_list.append(index_of(min(values), values))  # 这里插入的直接就是list1列表根据values列表排序规则排序后的索引？？values[index_of(min(values), values)] = math.inf# 这个函数会陷入死循环，所以我加了个if语句，当value全为inf时直接breakif set(values) == {math.inf}:breakreturn sorted_list# Function to carry out NSGA-II's fast non dominated sort
def fast_non_dominated_sort(values1, values2):''':param values1: 多目标优化问题中每个解在第一个目标函数下的取值，如[5, 2, 9, 3, 7, 4]:param values2: 多目标优化问题中每个解在第二个目标函数下的取值，如[6, 4, 8, 2, 5, 3]:return: 二维列表 front，其中包含 Pareto 前沿中每层非支配解的索引，如[[2], [0, 4], [1, 5], [3]]'''# 初始化 S, front, n 和 rank 列表S = [[] for _ in range(0, len(values1))]  # 记录每个解的被支配解集合front = [[]]  # 记录 Pareto 前沿层级n = [0 for _ in range(0, len(values1))]  # 记录每个解被支配的次数rank = [0 for _ in range(0, len(values1))]  # 记录每个解所处的 Pareto 前沿层级# 对每个解计算被支配解集合 S 和支配该解的次数 nfor p in range(0, len(values1)):S[p] = []n[p] = 0for q in range(0, len(values1)):if (values1[p] > values1[q] and values2[p] > values2[q]) or (values1[p] >= values1[q] and values2[p] > values2[q]) or (values1[p] > values1[q] and values2[p] >= values2[q]):if q not in S[p]:S[p].append(q)elif (values1[q] > values1[p] and values2[q] > values2[p]) or (values1[q] >= values1[p] and values2[q] > values2[p]) or (values1[q] > values1[p] and values2[q] >= values2[p]):n[p] = n[p] + 1# 如果一个解没有被任何其他解支配，则将其归为 Pareto 前沿的第一层if n[p] == 0:rank[p] = 0if p not in front[0]:front[0].append(p)# 循环计算 Pareto 前沿集合i = 0while front[i]:Q = []for p in front[i]:# 遍历被支配解集合 S，更新其 n 值for q in S[p]:n[q] = n[q] - 1# 如果某个解 q 不被其他解支配，则将其归为下一层 Pareto 前沿if n[q] == 0:rank[q] = i + 1if q not in Q:Q.append(q)i = i + 1# 将下一层 Pareto 前沿加入到 front 中front.append(Q)# 删除最后一个空元素del front[len(front) - 1]# 返回 Pareto 前沿集合return front# Function to calculate crowding distance
def crowding_distance(values1, values2, fronti):"""计算 Pareto 前沿中每个解的拥挤距离:param values1: 一个列表，表示所有解在目标函数 1 下的取值:param values2: 一个列表，表示所有解在目标函数 2 下的取值:param fronti: 一个列表，包含 Pareto 前沿中某一层的非支配解的索引:return 一个列表，表示 Pareto 前沿中每个解的拥挤距离"""distance = [0 for _ in range(0, len(fronti))]  # 初始化第i层所有解的拥挤距离为 0sorted1 = sort_by_values(fronti, values1[:])  # 根据目标函数 1 的取值，为当前前沿层排序并得到排序后的索引列表sorted2 = sort_by_values(fronti, values2[:])  # 根据目标函数 2 的取值，为当前前沿层排序并得到排序后的索引列表# 对于前沿中的第一个和最后一个解，将其拥挤距离设为一个较大的数distance[0] = 4444444444444444distance[len(fronti) - 1] = 4444444444444444# 计算前沿中其他解的拥挤距离if len(distance) <= 2:return distancefor k in range(1, len(fronti) - 1):# 按照目标函数 1 进行计算，并将结果加到该解的拥挤距离上distance[k] = distance[k] + (values1[sorted1[k + 1]] - values2[sorted1[k - 1]]) / (max(values1) - min(values1))# 按照目标函数 2 进行计算，并将结果加到该解的拥挤距离上distance[k] = distance[k] + (values1[sorted2[k + 1]] - values2[sorted2[k - 1]]) / (max(values2) - min(values2))return distance  # 返回所有解的拥挤距离列表# Function to carry out the crossover
def crossover(a, b):'''输入参数a和b是两个染色体，其中r是一个0到1之间的随机数。该函数根据随机数r的大小，选择将a和b进行加权平均或者差值运算，来生成新的染色体。然后，通过调用mutation函数对新的基因进行变异处理。'''r = random.random()if r > 0.5:return mutation((a + b) / 2)else:return mutation((a - b) / 2)# Function to carry out the mutation operator
def mutation(solution):'''输入参数solution是一个染色体。该函数根据mutation_prob的大小，决定是否对基因进行变异处理。mutation_prob是一个0到1之间的随机数，用来表示变异的概率。在这个函数中，如果mutation_prob小于1，则将solution的值替换为min_x和max_x之间的随机数。'''mutation_prob = random.random()     # 变异概率if mutation_prob < 1:   # 这里表示一定会变异solution = min_x + (max_x - min_x) * random.random()    # 随机替换掉一个x的取值return solution# Main program starts here
if __name__ == '__main__':pop_size = 20  # 种群大小max_gen = 921  # 最大迭代次数# Initializationmin_x = -55  # x的取值范围（定义域）max_x = 55solution = [min_x + (max_x - min_x) * random.random() for _ in range(0, pop_size)]  # 在最大值和最小值之间生成随机的x取值列表gen_no = 0  # 当前迭代次数while gen_no < max_gen:# 计算两个函数在当前x取值下的y值（y1、y2）function1_values = [function1(solution[i]) for i in range(0, pop_size)]function2_values = [function2(solution[i]) for i in range(0, pop_size)]# 对y1和y2两个列表进行非支配排序，返回帕累托前沿中每层非支配解的索引non_dominated_sorted_solution = fast_non_dominated_sort(function1_values[:], function2_values[:])# print("non_dominated_sorted_solution=", non_dominated_sorted_solution)print("The best front for Generation number ", gen_no, " is")for valuez in non_dominated_sorted_solution[0]:print(round(solution[valuez], 3), end=" ")  # 保留3位小数print("\n")crowding_distance_values = []   # 拥挤距离for i in range(0, len(non_dominated_sorted_solution)):crowding_distance_values.append(crowding_distance(function1_values[:], function2_values[:], non_dominated_sorted_solution[i][:]))solution2 = solution[:]     # 将x取值列表深拷贝给solution2# Generating offsprings# 将solution2进行交叉和变异生成子代，返回2*pop_size长度的新的solution2列表，前pop_size是父代，后pop_size是子代while len(solution2) != 2 * pop_size:a1 = random.randint(0, pop_size - 1)b1 = random.randint(0, pop_size - 1)solution2.append(crossover(solution[a1], solution[b1]))# 计算新的y1和y2列表（新解是由父代和子代拼接成的2*pop_size列表）function1_values2 = [function1(solution2[i]) for i in range(0, 2 * pop_size)]function2_values2 = [function2(solution2[i]) for i in range(0, 2 * pop_size)]# 对新的y1和y2列表进行非支配排序（父代+子代）non_dominated_sorted_solution2 = fast_non_dominated_sort(function1_values2[:], function2_values2[:])crowding_distance_values2 = []  # 新的拥挤距离（父代+子代）for i in range(0, len(non_dominated_sorted_solution2)):crowding_distance_values2.append(crowding_distance(function1_values2[:], function2_values2[:], non_dominated_sorted_solution2[i][:]))new_solution = []   #for i in range(0, len(non_dominated_sorted_solution2)): # front各层的索引non_dominated_sorted_solution2_1 = [index_of(non_dominated_sorted_solution2[i][j], non_dominated_sorted_solution2[i]) for j inrange(0, len(non_dominated_sorted_solution2[i]))]# 根据拥挤距离对非支配解的每一层进行排序front22 = sort_by_values(non_dominated_sorted_solution2_1[:], crowding_distance_values2[i][:])front = [non_dominated_sorted_solution2[i][front22[j]] for j inrange(0, len(non_dominated_sorted_solution2[i]))]front.reverse()     # 逆序，选择最末pop_size的front值（因为这里已经按照拥挤距离排序了，逆序表示选择拥挤距离较大的值，以尽可能保持解的多样性）for value in front:new_solution.append(value)if len(new_solution) == pop_size:breakif len(new_solution) == pop_size:breaksolution = [solution2[i] for i in new_solution]gen_no = gen_no + 1# 打印一下最终解的非支配排序结果看一下（结果发现所有的解都是非支配解。。。）# final_f1_values = [function1(solution[i]) for i in range(0, pop_size)]# final_f2_values = [function2(solution[i]) for i in range(0, pop_size)]# sort_result = fast_non_dominated_sort(final_f1_values,final_f2_values)# print(sort_result)# Lets plot the final front nowfunction1 = [i * -1 for i in function1_values]function2 = [j * -1 for j in function2_values]plt.xlabel('Function 1', fontsize=15)plt.ylabel('Function 2', fontsize=15)plt.scatter(function1, function2)plt.show()

这篇关于【调度算法】NSGA II的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---