本文主要是介绍论文笔记:Privacy-Preserving Deep Learning via Additively Homomorphic Encryption,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
论文笔记:Privacy-Preserving Deep Learning via Additively Homomorphic Encryption
- 论文介绍
- 问题背景
- 贡献
- 使用技术概述
- 时间开销
- 安全性和准确性
- 思考
- 技术概述
- 原始异步SGD
- SSL/TLS 协议
- 神经网络推理例子
- 随机梯度下降(SGD)
- 异步SGD
- 神经网络推理泄露信息
- 图b:不加噪声的图像成比例还原
- 图c:加入正则项的还原
- 图d:加入拉普拉斯噪声的还原
- 系统介绍
- 参与者1需要完成
- 每个参与者需要完成
- 基于LWE的梯度加密实现
- 背景
- 具体实现
- 数据编码和加密
- 安全性分析
论文介绍
Privacy-Preserving Deep Learning via Additively Homomorphic Encryption是TIFS信息安全顶会2018的论文
这篇论文目的是针对机器学习中的神经网络推理进行隐私保护
问题背景
海量数据收集虽然对深度学习至关重要,但也引发了隐私问题。单独地,收集的照片可以永久保存在公司服务器上,不受所有者的控制。从法律上讲,隐私和保密问题可能会阻止医院和研究中心共享他们的医疗数据集,使他们无法享受大规模深度学习优于联合数据集的优势。
为了保护隐私,Shokri和Shmatikov的系统保留了准确性/隐私权衡(见表I):不共享局部梯度会导致完美的隐私,但不会带来理想的准确性;另一方面,共享所有局部梯度会侵犯隐私,但会带来良好的准确性。为了折衷,共享一部分局部梯度是Shokri and Shmatikov的方案中保持最佳精度的主要解决方案。

贡献
使用技术概述
这篇论文结构比较明了,它针对机器学习中的神经网络推理进行隐私保护,就是异步随机梯度下降算法,用了一种密码学技术,加法同态加密。
我们的系统将深度学习和密码学联系起来:我们将异步随机梯度下降应用于神经网络,并结合加性同态加密。我们表明加密的使用给普通的深度学习系统增加了可容忍的开销。
时间开销
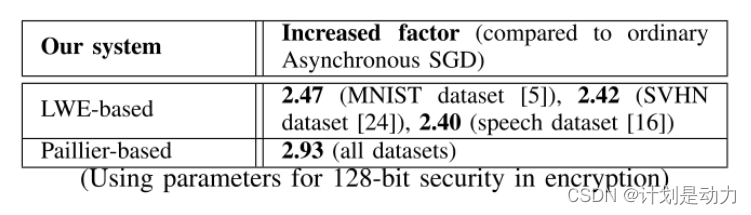
(表格里面的数字表示进行同态加密后需要传输数据的量的倍数)
例如,在MNIST的情况下,如果每个学习参与者需要在每次上传或下载时向服务器传送0.56 MB的普通梯度,那么在我们的系统使用基于错误学习(LWE)的加密时,在每次上传和下载时的相应通信成本变为:

这需要大约8毫秒才能在1Gbps信道上传输。
在计算方面,我们估计,当在MNIST数据集上进行训练和测试时,我们使用具有109386个梯度的多层感知器的系统在大约2.25小时内完成,以获得大约97%的准确度,这与给出的相同类型的神经网络的结果相匹配。此外,对于具有105506个梯度的MNIST,使用与Shokri and Shmatikov中相同的卷积神经网络,我们估计我们的系统在大约7.3小时内完成(由于定理2,精度与Shokri and Shmatikov的精度大约99%相同)。
安全性和准确性
我们表明准确性/隐私之间的权衡可以转移到我们系统中的效率/隐私。因为准确性/隐私权衡可能会使保护隐私的深度学习不如普通的深度学习更有吸引力,因为准确性是该领域的主要吸引力。
如果采用更多的处理单元和更多的专用编程代码,我们的效率/隐私权衡(保持普通的深度学习精度不变)可以得到改善。
在安全性和准确性方面具有以下特点:
Security. 系统不会向诚实但好奇的参数(云)服务器泄露参与者的信息。
Accuracy. 系统达到与所有参与者联合数据集上训练的相应深度学习系统(异步随机梯度下降,见下文)相同的精度。
简言之,系统在这两个方面都享有最好的优势:安全性如密码学,精确性如深度学习。
思考
如果假设参与者都是诚实的话,会有一些隐藏的安全问题,如果有恶意节点的话可能会导致隐私泄露,所以这篇论文存在一些改进的空间:如何实现多方节点的秘钥共享?
技术概述
原始异步SGD
在不考虑隐私保护的情况下:
首先随机初始化神经网络的全局权重向量Wglobal。然后,在每次迭代中,在本地数据集上运行神经网络的副本(即数据并行性),并将相应的本地梯度向量Glocal发送到云服务器。对于每个Glocal,云服务器随后更新全局参数,如下所示:
W g l o b a l : = W g l o a b a l − α ⋅ G l o c a l ( 1 ) W_{global} := W_{gloabal} - α · G_{local} \ \ (1) Wglobal:=Wgloabal−α⋅Glocal (1)
其中α是学习率。更新的全局参数Wglobal被广播给所有副本,然后副本使用它们来替换其旧的权重参数。重复更新和广播Wglobal的过程,直到达到预定义loss函数(基于交叉熵或平方误差)的期望最小值。
对于模型并行性,通过向量Wglobal和Glocal的分量并行计算(1)的更新。
引入隐私保护的ASGD(选择性SGD)
W g l o b a l : = W g l o a b a l − α ⋅ G l o c a l s e l e c t i v e ( 2 ) 其中 G l o c a l s e l e c t i v e 包含 G l o c a l 的选择性梯度 ( e g . 1 % ~ 100 % ) W_{global} := W_{gloabal} - α · G_{local}^{selective} \ \ (2) \\其中G_{local}^{selective}包含Glocal的选择性梯度(eg.1\%~100\%) Wglobal:=Wgloabal−α⋅Glocalselective (2)其中Glocalselective包含Glocal的选择性梯度(eg.1%~100%)
使用(2)的更新允许每个参与者选择要在全球共享的梯度,希望减少将参与者本地数据集上的敏感信息泄漏到云服务器的风险。
Shokri Shmatikov展示了一种使用差异隐私来抵消梯度间接泄漏的额外技术。他们的策略是
在 ( 2 ) 处的 G l o c a l s e l e c t i v e 中添加 L a p l a c e n o i s e 在(2)处的G_{local}^{selective}中添加Laplace \ noise 在(2)处的Glocalselective中添加Laplace noise
我们的系统:我们的系统可以称为梯度加密ASGD
由于噪声,这种方法损害了学习精度(深度学习的主要吸引力)。
3) 我们的系统:我们的系统可以称为梯度加密ASGD,原因如下。在第四节的系统中,我们使用以下更新公式
E ( W g l o b a l ) : = E ( W g l o b a l ) + E ( − α ⋅ G l o c a l ) E(W_{global}) := E(W_{global}) + E(-α·G_{local}) E(Wglobal):=E(Wglobal)+E(−α⋅Glocal)
其中E是支持密文上的加法的同态加密。解密密钥只有参与者知道,而云服务器不知道。
因此,最诚实但好奇的云服务器对每个 G l o c a l 一无所知 因此无法获得每个参与者的本地数据集的信息。 因此,最诚实但好奇的云服务器对每个G_{local}一无所知\\因此无法获得每个参与者的本地数据集的信息。 因此,最诚实但好奇的云服务器对每个Glocal一无所知因此无法获得每个参与者的本地数据集的信息。
尽管如此,作为:
E ( W g l o b a l ) + E ( − α ⋅ G l o c a l ) = E ( W g l o b a l − α ⋅ G l o c a l ) E(W_{global})+E(-α·G_{local})=E(W_{global}−α·G_{local}) E(Wglobal)+E(−α⋅Glocal)=E(Wglobal−α⋅Glocal)
通过 E 的加同态性质,每个参与者将通过解密获得正确更新的 W g l o b a l 通过E的加同态性质,每个参与者将通过解密获得正确更新的W_{global} 通过E的加同态性质,每个参与者将通过解密获得正确更新的Wglobal
此外,为了确保同态密文的完整性,每个客户端将使用一个安全通道,如TLS/SSL(彼此不同)来与服务器通信同态密文。
SSL/TLS 协议
SSL/TLS 协议位于网络 OSI 七层模型的会话层,用来加密通信。
SSL(Secure Sockets Layer,安全套接字层)是一种标准安全协议,用于在在线通信中建立Web服务器和浏览器之间的加密链接。
SSL 通过互相认证、使用数字签名确保完整性、使用加密确保私密性,以实现客户端和服务器之间的安全通讯。
TLS(Transport Layer Security,传输层安全)是 IETF 在 SSL 3.0 的基础上设计的协议,它是 SSL 协议的升级版。两者差别极小,可以理解为 TLS 是 SSL 3.1。
TLS 记录协议负责消息的压缩、加密以及数据的认证。TLS 记录协议使用到的所有的算法等都是经过握手协议协商确认后的,以保证通讯双方是使用相同的算法。处理过程:
- 首先,消息会被分割成多份,并用协商好的压缩算法进行压缩。
- 其次,压缩片段会加上消息认证码以保证完整性,为了防止重放攻击还加上了片段编号。
- 再次,压缩后的消息片段会加上消息认证码一起进行加密。加密使用 CBC 模式,初始向量是通过主密码生成。
- 最后,加密后的报文,再加上数据类型、版本号、压缩后的长度组成的报头,就是最终的数据报文。
神经网络推理例子

每个神经元节点(除了偏置节点)与激活函数f相关联。
eg.
f ( z ) = m a x { 0 , z } f ( z ) = e z − e − z e z + e − z f ( z ) = 1 1 + e − z ( s i g m o i d ) 神经网络基本推导过程: a ( l + 1 ) = f ( W ( l ) a ( l ) + b ( l ) ) ( W ( l ) , b ( l ) ) 是连接层 l 和 l + 1 的权重 , a ( l ) 是层 l 的输出 f(z) = max\{0,z\} \\f(z) = \frac{e^z-e^{-z}}{e^z+e^{-z}} \\f(z)=\frac{1}{1+e^{-z}} \ \ \ \ (sigmoid) \\神经网络基本推导过程: a^{(l+1)} = f(W^{(l)}a^{(l)}+b^{(l)}) \\(W^{(l)},b^{(l)})是连接层l和l+1的权重,a^{(l)}是层l的输出 f(z)=max{0,z}f(z)=ez+e−zez−e−zf(z)=1+e−z1 (sigmoid)神经网络基本推导过程:a(l+1)=f(W(l)a(l)+b(l))(W(l),b(l))是连接层l和l+1的权重,a(l)是层l的输出
给定训练数据集,学习任务是确定这些权重变量,以最小化预定义的成本函数,如交叉熵或平方误差成本函数。
神经网络可以通过一个称为异步SGD进行训练,具有数据并行性和模型并行性的特性。具体来说,首先对神经网络的全局权重向量W进行随机初始化。可以对训练数据集中的所有数据项计算loss函数,或者在来自训练数据集的t个元素的子集(称为小batch)上计算loss。
成本函数 J ∣ b a t c h ∣ = t 成本函数J_{|batch|} = t 成本函数J∣batch∣=t
随机梯度下降(SGD)
设W是由所有权重变量组成的展平向量。也就是说,我们取神经网络中的所有权重,并连续排列它们以形成向量W。
设 W = ( W 1 , . . W n g d ) ∈ R n g d 让 G = ( δ J ∣ b a t c h ∣ = t δ W 1 , . . . δ J ∣ b a t c h ∣ = t δ W n g d ) 对应 变量 W 1 , … W n g d 的 l o s s 函数 J ∣ b a t c h ∣ = t 的梯度 设W = (W_1,..W_{n_{gd}}) \in \R^{n_{gd}} \\让G=(\frac{\delta_{J_{|batch|} = t}}{\delta W_1},...\frac{\delta_{J_{|batch|} = t}}{\delta W_{n_{gd}}})对应 \\变量W_1,…W_{{n_{gd}}}的loss函数J|batch|=t的梯度 设W=(W1,..Wngd)∈Rngd让G=(δW1δJ∣batch∣=t,...δWngdδJ∣batch∣=t)对应变量W1,…Wngd的loss函数J∣batch∣=t的梯度
对于学习率 α ∈ R , S G D 中的变量更新规则如下: W : = W − α ⋅ G 其中 α ⋅ G 是分量乘法 α ⋅ G = ( α G 1 , … , α G n g d ) ∈ R n g d 对于学习率α∈\R,SGD中的变量更新规则如下: \\W:= W- α·G \\其中α·G是分量乘法α·G=(αG_1,…,αG_{n_{gd}})∈\R^{n_{gd}} 对于学习率α∈R,SGD中的变量更新规则如下:W:=W−α⋅G其中α⋅G是分量乘法α⋅G=(αG1,…,αGngd)∈Rngd
异步SGD

异步SGD使用神经网络的多个副本。在每次执行之前,每个副本都将从参数服务器下载最新的权重W,并且每个神经网络副本都在一个在本地数据集(数据并行性)上运行,生成本地梯度向量G,发送到云服务器。
服务器具有多个处理单元
P U 1 , . . . P U n p u PU_1,...PU_{n_{pu}} PU1,...PUnpu
由于处理单元可以并行运行,所以这里将其权重向量W和梯度G拆分为npu个部分
W = ( W ( 1 ) , . . . , W ( n p u ) ) G = ( G ( 1 ) , . . . , G ( n p u ) ) W = (W^{(1)},...,W^{(n_{pu})}) \\G=(G^{(1)},...,G^{(n_{pu})}) W=(W(1),...,W(npu))G=(G(1),...,G(npu))
显著提高了深度网络训练的规模和速度。
对于每个wi和G i,云服务器的处理单元PUi都会计算
W ( i ) : = W ( i ) − α ⋅ G ( i ) W^{(i)} := W^{(i)} - α·G^{(i)} W(i):=W(i)−α⋅G(i)
来更新全局权重向量参数w,其中α是学习率。
更新后的全局权重参数W将广播到所有副本,然后这些副本用它来替换旧的权重参数。这种更新和广播W的过程一直重复,直到损失函数达到理想状态。
神经网络推理泄露信息
下面作者举了几个例子表示梯度会泄露信息,而且现有的梯度保护的系统并不能有效地保护数据信息。
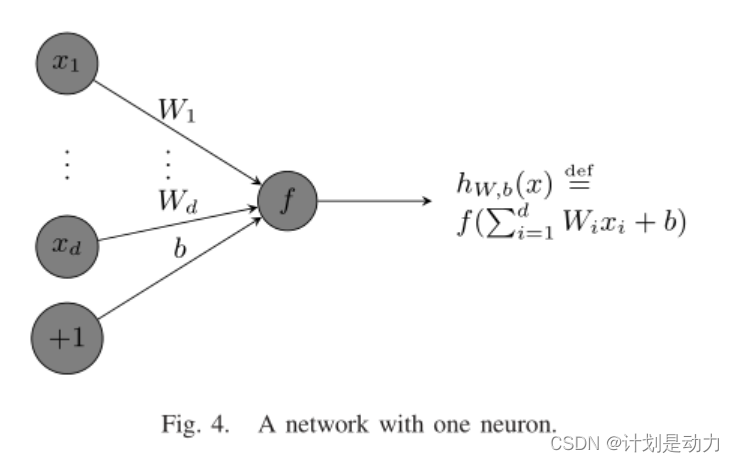
在图中,实数 x i ( 1 ≤ i ≤ d ) 是输入数据,具有相应的真值标签 y 实数 W i ( 1 ≤ i ≤ d ) 是要学习的权重参数; b 是偏置。 函数 f 是一个激活函数 l o s s : J ( W , b , x , y ) = d e f ( h w , b ( x ) − y ) 2 在图中,实数x_i(1≤i≤d)是输入数据,具有相应的真值标签y \\实数W_i(1≤i≤d)是要学习的权重参数;b是偏置。 \\函数f是一个激活函数 \\loss :J(W,b,x,y) \overset{def}= (h_{w,b}(x)-y)^2 在图中,实数xi(1≤i≤d)是输入数据,具有相应的真值标签y实数Wi(1≤i≤d)是要学习的权重参数;b是偏置。函数f是一个激活函数loss:J(W,b,x,y)=def(hw,b(x)−y)2
主要原因是下面这两条ηk / η。ηk / η都是梯度,xk是输入x中的第k个元素。
η k = d e f δ J ( W , b , x , y ) δ W k = 2 ( h W , b ( x ) − y ) δ h w , b ( x ) δ W k = 2 ( h w , b ( x ) − y ) δ f ( ∑ i = 1 d W i x i + b ) δ W k = 2 ( h w , b ( x ) − y ) f ′ ( ∑ i = 1 d W i x i + b ) ⋅ x k η = d e f δ J ( W , b , x , y ) δ b = 2 ( h w , b ( x ) − y ) δ h W , b ( x ) δ b = 2 ( h w , b ( x ) − y ) δ f ( ∑ i = 1 d W i x i + b ) δ b = 2 ( h w , b ( x ) − y ) f ′ ( ∑ i = 1 d W i x i + b ) ⋅ 1 ∴ η k η = x k \eta_k \overset{def}= \frac{\delta J(W,b,x,y)}{\delta W_k}=2(h_{W,b}(x)-y)\frac{\delta h_{w,b}(x)}{\delta W_k}\\=2(h_{w,b}(x)-y)\frac{\delta f(\sum_{i=1}^dW_ix_i+b)}{\delta W_k}\\=2(h_{w,b}(x)-y)f'(\sum_{i=1}^dW_ix_i+b)·x_k \\ \\ \eta \overset{def}{=}\frac{\delta J(W,b,x,y)}{\delta b}=2(h_{w,b}(x)-y)\frac{\delta h_{W,b}(x)}{\delta b}\\=2(h_{w,b}(x)-y)\frac{\delta f(\sum_{i=1}^dW_ix_i+b)}{\delta b} \\=2(h_{w,b}(x)-y)f'(\sum_{i=1}^dW_ix_i+b)·1 \\ \\ ∴\frac{\eta_k}{\eta}=x_k ηk=defδWkδJ(W,b,x,y)=2(hW,b(x)−y)δWkδhw,b(x)=2(hw,b(x)−y)δWkδf(∑i=1dWixi+b)=2(hw,b(x)−y)f′(i=1∑dWixi+b)⋅xkη=defδbδJ(W,b,x,y)=2(hw,b(x)−y)δbδhW,b(x)=2(hw,b(x)−y)δbδf(∑i=1dWixi+b)=2(hw,b(x)−y)f′(i=1∑dWixi+b)⋅1∴ηηk=xk
- 因此,如果ηk和η被共享到云服务器,xk将完全泄漏。
尽管现有梯度保护方案中,建议是随机选择1%的本地梯度共享给服务器,那么ηk和η共享的概率是
1 100 × 1 100 = 1 10000 \frac{1}{100} \times\frac{1}{100} = \frac{1}{10000} 1001×1001=100001
这个一万分之一是不可忽略的,这是存在一个概率泄露输入的。
-
注意到梯度ηk与输入xk成正比(对所有的1 ≤ i ≤ d)。
因此,当x =(x1,…,xd)是一张图像时,可以使用梯度生成相关的“成比例”图像,然后通过猜测获得真实值y

图a是原数据图像,bcd都是通过梯度恢复出来的图像。
图b是经过一般的神经网络训练过程中得到的梯度恢复出来的图像
c是带有正则化操作的神经网络的梯度恢复出来的图像
d是加了Laplace噪声的神经网络的梯度恢复出来的图像。
从图中可以看到,正则化和加Laplace噪声会有一些作用,但是恢复出来的图像依然能够辨识,能够看出它的真实值y,也就是图中这个0。
如果Laplace的噪声加的再多,那么确实无法从梯度上恢复出图像信息,但是过多的噪声会导致这个权值不可用,对准确率造成影响。
在神经网络中:
η i k = d e f δ J ( W , b , x , y ) δ W i k ( 1 ) = ξ i ⋅ x k ( 9 ) 其中 δ W i k ( 1 ) 是连接层 1 的输入 x k 链接层 2 的隐藏节点 i 的权重参数 ξ i 是一个实数。 η_{ik} \overset{def}= \frac{δ J(W, b, x, y)} {δW^{(1)} _{ik}} = ξ_i · x_k \ \ (9) \\其中δW^{(1)}_{ik}是连接层1的输入x_k链接层2的隐藏节点i的权重参数\\ξ_i是一个实数。 ηik=defδWik(1)δJ(W,b,x,y)=ξi⋅xk (9)其中δWik(1)是连接层1的输入xk链接层2的隐藏节点i的权重参数ξi是一个实数。
图b:不加噪声的图像成比例还原

在图(b)中,使用Fig 1上的神经网络,我们证明了上面的梯度确实与原始数据成比例,因为图3(b)与图3(a)仅在值栏处不同。
原始数据是一个20x20的图像,重新整形为
( x 1 , … , x 400 ) ∈ R 400 (x_1,…,x_{400})∈\R^{400} (x1,…,x400)∈R400
的向量。该向量是对由25个节点组成的1个隐藏层的神经网络的输入,并且输出层包含10个节点。所以神经网络中的梯度总数为:
( 400 + 1 ) × 25 + ( 25 + 1 ) × 10 = 10285 ( + 1 是 b 代表梯度 ) (400+1)\times25+(25+1)\times10 =10285 \\(+1是b代表梯度) (400+1)×25+(25+1)×10=10285(+1是b代表梯度)
在(9)中,我们有1≤k≤400和1≤i≤25。然后,我们使用(9)处的一小部分梯度,即
( η 1 k ) 1 ≤ k ≤ 400 1 ≤ i ≤ 25 (η_{1k}) \ 1≤k≤400 \ 1≤i≤25 (η1k) 1≤k≤400 1≤i≤25
将其重塑为20x20的图像,以绘制图(b)。
很明显,梯度的部分(即400/10285≈3.89%)揭示了原始数据的真值标签0。
图c:加入正则项的还原

引入正则项λ:
η i k = d e f δ J ( W , b , x , y ) δ W i k ( 1 ) = ξ i ⋅ x k + λ W i k ( 1 ) η i = d e f δ J ( W , b , x , y ) δ b i ( 1 ) = ξ i ∴ η i k η i = x k + λ W i k ( 1 ) ξ i λ W i k ( 1 ) ξ i 记作噪声 , 把该值作为 x k 的近似值 η_{ik} \overset{def}= \frac{δ J(W, b, x, y)} {δW^{(1)}_{ik}}= ξ_i · x_k + \lambda W^{(1)}_{ik} \\η_{i} \overset{def}= \frac{δ J(W, b, x, y)} {δb^{(1)}_{i}}= ξ_i \\∴\frac{\eta_{ik}}{\eta_i} = x_k + \frac{\lambda W_{ik}^{(1)}}{ξ_i} \\\frac{\lambda W_{ik}^{(1)}}{ξ_i}记作噪声,把该值作为x_k的近似值 ηik=defδWik(1)δJ(W,b,x,y)=ξi⋅xk+λWik(1)ηi=defδbi(1)δJ(W,b,x,y)=ξi∴ηiηik=xk+ξiλWik(1)ξiλWik(1)记作噪声,把该值作为xk的近似值
图d:加入拉普拉斯噪声的还原

将平均值为0的拉普拉斯噪声和导数σ=1/100添加到梯度
η i k = ξ i ⋅ x k + L a p l a c e ( 0 , 1 100 ) \eta_{ik} = ξ_i · x_k + Laplace(0, \frac{1}{100}) ηik=ξi⋅xk+Laplace(0,1001)
图像包含噪声,但仍然可以看到真实值。此外,当参数σ较大时,ηik可能受噪声支配,因此很难看到真值标签,但这可能无助于更新权重变量,影响原来的模型训练。
系统介绍
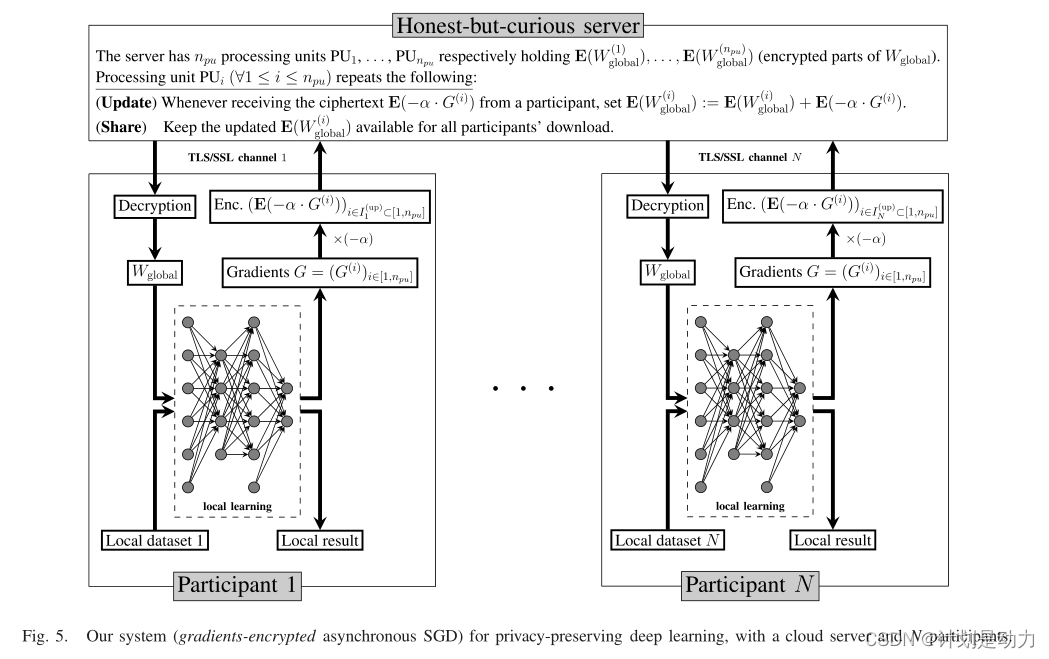
由一个公共云服务器和N个(e.g.=10~100)学习参与者组成
参与者共同设置用于加性同态加密方案的公钥pk和密钥sk,以实现同态加密方案。密钥sk对云服务器保密,但所有学习参与者都知道。
每个参与者建立一个相互不同的TLS/SSL安全通道,以进行通信并保护同态密文的完整性。然后,参与者在本地保存他们的数据集,并运行基于深度学习的神经网络的副本。
参与者1需要完成
运行局部神经网络的初始(随机)权重Wglobal由参与者1初始化,还需发送:
E ( W g l o b a l ( 1 ) , . . , W g l o b a l ( n ) ) W g l o b a l ( i ) 就是构成 W g l o b a l 第 i 部分的向量 E(W_{global}^{(1)},..,W_{global}^{(n)}) \\W_{global}^{(i)}就是构成W_{global}第i部分的向量 E(Wglobal(1),..,Wglobal(n))Wglobal(i)就是构成Wglobal第i部分的向量
到服务器
在每次执行神经网络之后获得的向量G被分割成n个pu部分:
G = ( G ( 1 ) , . . . , G ( n p u ) ) G=(G^{(1)},...,G^{(n_{pu})}) G=(G(1),...,G(npu))
乘以学习率α,然后使用公钥pk进行加密
来自每个学习参与者的最终加密
E ( − α ⋅ G ( i ) ) ( ∀ 1 ≤ i ≤ n p u ) E(-\alpha·G^{(i)}) \ \ (∀1≤i≤n_{pu}) E(−α⋅G(i)) (∀1≤i≤npu)
被发送到服务器的处理单元PUi,还值得注意的是,学习率α可以在每个学习参与者处自适应地局部改变
每个参与者需要完成
如图所示,每个参与者1≤k≤N将执行以下步骤:
- 从PUj下载密文
E ( W g l o b a l ( j ) ) j ∈ I k ( d o w n ) ⊂ [ 1 , n p u ] I k ( d o w n ) ⊂ [ 1 , n p u ] 的原因是部分学习参与者的下载带宽受到限制 E(W_{global}^{(j)}) \ \ j\in I_k^{(down)}⊂[1,n_{pu}] \\ I_k^{(down)}⊂[1,n_{pu}]的原因是部分学习参与者的下载带宽受到限制 E(Wglobal(j)) j∈Ik(down)⊂[1,npu]Ik(down)⊂[1,npu]的原因是部分学习参与者的下载带宽受到限制
- 使用密钥sk解密上述密文
获取 W g l o b a l ( j ) j ∈ I k ( d o w n ) 获取W_{global}^{(j)} \ \ j\in I_k^{(down)} 获取Wglobal(j) j∈Ik(down)
-
从其本地数据集中获取一小批数据
-
使用步骤2和3中的Wglobal和数据项的值,计算梯度
G = ( G ( 1 ) , . . . , G ( n p u ) ) 相对于变量 W g l o b a l G=(G^{(1)},...,G^{(n_{pu})})相对于变量W_{global} G=(G(1),...,G(npu))相对于变量Wglobal -
加密并发回密文
E ( − α G ( i ) ) ∀ i ∈ I k ( u p ) ⊂ [ 1 , n p u ] I k 取决于参与者 k 的选择 如果 I k ( u p ) = [ 1 , n p u ] 就是将所有加密的梯度上传到服务器 E(-\alpha G^{(i)}) \ \ ∀i\in I_k^{(up)}⊂ [1, n_{pu}] \\I_k取决于参与者k的选择\\如果I_k^{(up)}= [1, n_{pu}]就是将所有加密的梯度上传到服务器 E(−αG(i)) ∀i∈Ik(up)⊂[1,npu]Ik取决于参与者k的选择如果Ik(up)=[1,npu]就是将所有加密的梯度上传到服务器
发送到服务器的相应处理单元PUi
Wglobal加密部分的下载和上传可以在两个方面异步:参与者彼此独立;并且处理单元也彼此独立
基于LWE的梯度加密实现
背景
A是公共参数
b = A s + e b = As + e b=As+e
每次选取的s和e是随机的,所以计算的b是一次一幂的

困难问题在于:
- 已知a和b很难计算出s
- 决策性问题:算一个b和在域里随机选取的b`无法区分
基于LWE的加法同态
首先模型的聚合或者或是梯度的聚合本质上就是向量的加法


LWE具有加法同态性,满足梯度的聚合条件
不使用LWE的情况下也可以实现加密

随机选取向量b作为掩码来加上我们的梯度x,我们聚合b+x后我要消掉b,而b的维度远大于s,所以将b进行传输不划算,传输s更划算
步骤:
- b作为掩码加上梯度x
- 只通讯低维度的私钥,走一个安全多方的求和协议来恢复出A*s

各参与方先对明文加扰动,这个扰动是全局扰动的一部分,比较小,有泄露的风险
我们可以通过去蓝色框*红色框减就可以得到扰动,将若干扰动求和聚合起来成为全局差分隐私


具体实现
标记 ← g 用于从离散高斯分布中随机采样 这意味着 x ← g Z ( 0 , s ) 出现的概率与 e ( − π x 2 / s 2 ) 成比例 标记\overset{g}← 用于从离散高斯分布中随机采样 \\这意味着x\overset{g}← \Z_{(0,s)} 出现的概率与e^{(-πx^2/s^2)}成比例 标记←g用于从离散高斯分布中随机采样这意味着x←gZ(0,s)出现的概率与e(−πx2/s2)成比例
- ParamGen 初始化
固定 q = q ( λ ) ∈ Z + 和 l ∈ Z + 固定 p ∈ Z + 使得 g c d ( p , q ) = 1 ( p q 互质 ) 返回 p p = ( q , l , p ) 固定q=q(\lambda) \in \Z^+ 和 l \in \Z^+ \\固定p\in \Z^+使得gcd(p,q) = 1 \ \ (pq互质) \\返回pp = (q,l,p) 固定q=q(λ)∈Z+和l∈Z+固定p∈Z+使得gcd(p,q)=1 (pq互质)返回pp=(q,l,p)
- KeyGen 秘钥生成
构造 L W E 难题: b = A s + e 取 s = s ( λ , p p ) ∈ R + a n d n l w e ∈ Z + 取 R , S ← g Z ( 0 , s ) n l w e × l , A ← g Z q n l w e × n l w e 计算 P = p R − A S ∈ Z q n l w e × l 返回公钥 p k = ( A , P , n l w e , s ) 和私钥 s k = S \\构造LWE难题:b = As + e\\ 取s = s(\lambda,pp) \in \R^+ and \ n_{lwe} \in \Z^+ \\取R,S\overset{g}← \Z_{(0,s)}^{n_{lwe}\times l},A\overset{g}←\Z_{q}^{n_{lwe}\times n_{lwe}} \\计算P = pR - AS \in \Z_{q}^{n_{lwe}\times l} \\返回公钥pk = (A,P,n_{lwe},s)和私钥sk=S 构造LWE难题:b=As+e取s=s(λ,pp)∈R+and nlwe∈Z+取R,S←gZ(0,s)nlwe×l,A←gZqnlwe×nlwe计算P=pR−AS∈Zqnlwe×l返回公钥pk=(A,P,nlwe,s)和私钥sk=S
- 加密Enc
取 e 1 , e 2 ← g Z ( 0 , s ) 1 × n l w e , e 3 ← g Z ( 0 , s ) 1 × l 计算 c 1 = e 1 A + p e 2 ∈ Z q 1 × n l w e c 2 = e 1 P + p e 3 + m ∈ Z q 1 × l 返回 c = ( c 1 , c 2 ) 取e_1,e_2\overset{g}←\Z_{(0,s)}^{1\times n_{lwe}},e_3\overset{g}←\Z_{(0,s)}^{1\times l} \\计算c_1 = e_1A+pe_2 \in \Z_q^{1\times n_{lwe}} \\c_2 = e_1P+pe_3+m\in \Z_q^{1\times l} \\返回c = (c_1,c_2) 取e1,e2←gZ(0,s)1×nlwe,e3←gZ(0,s)1×l计算c1=e1A+pe2∈Zq1×nlwec2=e1P+pe3+m∈Zq1×l返回c=(c1,c2)
- 解密Dec
计算 m − = c 1 S + c 2 ∈ Z q 1 × l 返回 m = m − m o d p 计算\overset{-}m=c_1S+c_2 \in \Z_q^{1\times l} \\返回m = \overset{-}m\ mod \ p 计算m−=c1S+c2∈Zq1×l返回m=m− mod p
- 同态加密Add(c,c‘)
额外的,计算并返回 c a d d = c + c ′ ∈ Z q 1 × ( n l w e + l ) 额外的,计算并返回c_{add}= c+c' \in \Z_q^{1\times (n_{lwe} +l)} 额外的,计算并返回cadd=c+c′∈Zq1×(nlwe+l)
数据编码和加密
可以用精度为prec位的实数A∈R来表示
安全性分析
安全性:系统没有向诚实但好奇的云服务器泄露学习参与者的信息,前提是同态加密方案是CPA(选择明文攻击)安全的。因为参与者只向云服务器发送加密的梯度。因此,如果加密方案是CPA安全的,那么参与者的数据就不会泄露任何信息。
准确性:只要所有的梯度都被上传和下载,所有的密文都被正确解密,那么这个系统就和一般的异步随机梯度下降算法的准确率没有差别。

下面是作者对他这个系统的一个实例化操作,用了两种,上述是基于LWE的加密,
第二个就是基于paillier的加密:
例如对一个矩阵向量进行同态加密运算的:
对于一个小数,把他表示为一个整数的形式,通过这个r乘上2的精度次方
因为公钥是n,所以明文空间是log2底n
所以可以把一些非负整数打包到一个密文里面。这里的填充0是为了防止在密文相加运算时导致溢出的。所以精度+填充位就是一个明文元素的长度,用明文空间long2底n相比,得到t就是将这些整数打包为一个Paillier明文的上限对于处理单元PUi,她的权值wi和梯度gi都包含有li个元素,在这把它表示为向量r,r有元素r1,r2 到rli,将其中t个为一组,一起进行加密。
因为是同态加法,这种打包成一个密文的方法不会影响加法计算,解密的时候再分开就可以了.

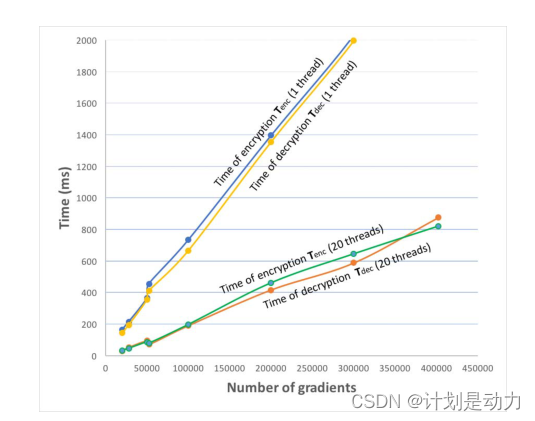
表3给出了不同梯度ngd的数量,加密、解密和加法的时间,看到时间与梯度数量是相关的。使用n_lwe=3000,s=8,p=2^48+1和q=277。
图5分别描述了使用1个线程和20个计算线程进行加密和解密的时间
这篇关于论文笔记:Privacy-Preserving Deep Learning via Additively Homomorphic Encryption的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







