Romberg算法代码实现

本文主要是介绍Romberg算法代码实现，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

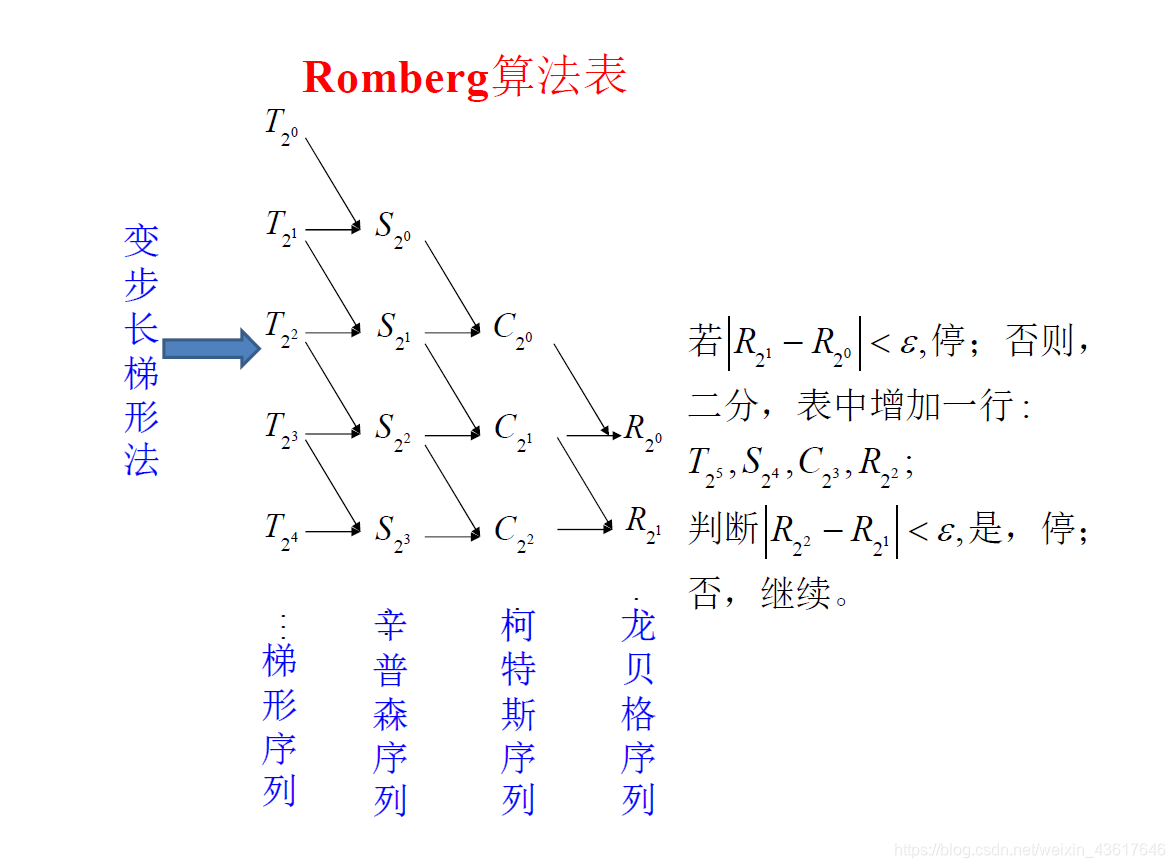
基于函数F(x)的求积函数，利用龙贝格方法进行求解：
在这里插入图片描述

# -*- coding: utf-8 -*-
"""
Created on Sun Jul  4 14:05:58 2021@author: wu
"""## 利用Romberg方法给定求解精度求解积分，并进行按行展示import pandas as pd
import torch
import math
import numpy as np# 被积函数f(x)
def fx(x):return 2*math.pi*x*math.exp(x**2)# 主函数
T = []
S = []
C = []
R = []a,b = 0 ,1  ##给定积分区间 和 误差
error = 10**(-6) 
t = torch.tensor(0.5*(b-a)*(fx(b))+fx(a))  #T0
T.append(t)for k in range(1,100):  #误差足够时直接跳出循环即可cash_file = 0   for i in range(2**(k-1)):cash_file = fx(a + (2*i+1)*(b-a)*0.5**(k)) + cash_filet = 0.5*T[k-1] + cash_file*0.5**(k)T.append(t) s = 4/3*T[k] - 1/3*T[k-1]S.append(s)if k >= 2:c = 16/15*S[k -1] - 1/15*S[k- 2]C.append(c)if k >= 3:r = 64/63*C[k -2] - 1/63*C[k- 3]R.append(r)if k >= 4:if R[k-3] - R[k-4] <= error:print("the similar value is :{}".format(R[k-3]))breakprint("--------------------------------------")
## 利用Pandas进行数据展示
con1 = np.array(T).reshape(-1,1)
S.insert(0, 0)
con2 = np.array(S).reshape(-1,1)
C.insert(0, 0)
C.insert(0, 0)
con3 = np.array(S).reshape(-1,1)
R.insert(0, 0)
R.insert(0, 0)
R.insert(0, 0)
con4 = np.array(R).reshape(-1,1)
List = pd.DataFrame(pd.concat([pd.DataFrame(con1),pd.DataFrame(con2),pd.DataFrame(con3),pd.DataFrame(con4)],1))
List.columns = ('Tn',"Sn","Cn","Rn")
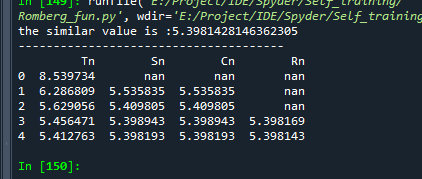
List.loc[0,'Sn':'Rn'] = List.loc[0:2,'Rn'] ='nan'print(List)

运行结果：
在这里插入图片描述