本文主要是介绍Romberg积分法Matlab代码实现及示例,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一.通用程序
function [I,eror,Rec] = Romberg(a,b,f,eps,option)
%-------------函数输出值说明-----------------
%-------- I:积分近似值
%-------- eror:截断误差
%-------- Rec:记录运算过程的矩阵%-------------函数参数说明-------------------
%-------- (a,b):积分区间
%-------- f:被积函数
%-------- eps: 精度
%-------- option: 为1则输出运算过程
if ~exist('option','var')option = 0;
end
x = [a,b]; %求积节点
h = b-a; %步长
T1 = (b-a)/2*(f(a)+f(b)); %T1T = T1;%复化梯形公式
S = [];%复化Simpson公式
C = [];%复化Cotes公式
R = [];%复化Romberg公式n = 1; %计算次数
choice = 1; %记录满足精度要求的终止点
eror = 1; %初始化循环变量
while eror>epsN = 2^n; %T_N中的N%生成新的求积节点x_mid = (x(1:end-1)+x(2:end))/2;%计算新的T_NT(end+1) = 1/2*(T(n)+h*sum(f(x_mid)));x = sort([x, x_mid]); %更新xh = (b-a)/N; %更新h%Romberg积分方法计算积分近似值if n>=1 %计算S_NS(end+1) = 4/3*T(n+1)-1/3*T(n);endif n>=2 %计算C_NC(end+1) = 16/15*S(n) -1/15*S(n-1);endif n>=3 %计算R_NR(end+1) = 64/63*C(n-1) - 1/63*C(n-2);end%计算误差switch ncase 1eror = 1/3*abs(T(end)-T(end-1));choice = 1;case 2eror = 1/15*abs(S(end)-S(end-1));choice = 2;case 3eror = 1/63*abs(C(end)-C(end-1));choice = 3;otherwiseeror = 1/255*abs(R(end)-R(end-1));choice = 4;endn = n+1; %循环次数+1
end
%选择输出结果
switch choicecase 1I = S(end);case 2 I = C(end);case {3,4}I = R(end);
end
%选择是否输出计算过程
if option ==1S = double(vpa([S,zeros(1,1)],6));C = double(vpa([C,zeros(1,2)],6));R = double(vpa([R,zeros(1,3)],6));%以矩阵形式呈现运算过程Rec = [T' S' C' R'];disp('运算过程-矩阵');disp(' T_n S_n C_n R_n');disp(Rec);
endend
二.示例
计算 的近似值,精确至7位有效数字
%积分限以及被积函数
a = 1;b = 5;
f = @(x)(sin(x)./x);
eps = 0.5e-7;%精度
[I,eror] = Romberg(a,b,f,eps,1);
disp('积分近似值:');
disp(vpa(I,7));
disp('截断误差:');
disp(eror);输出结果:
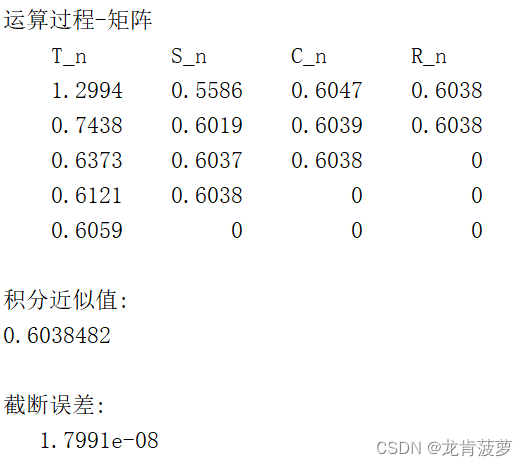
注:Romberg()函数中的参数f,涉及到乘除运算时相应使用.*、./,这一点可以从通用程序计算T_n的代码中可以看出。
这篇关于Romberg积分法Matlab代码实现及示例的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



