本文主要是介绍(八)锥桶赛道路径规划,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1、参考资料
三角剖分:https://blogs.mathworks.com/student-lounge/2022/10/03/path-planning-for-formula-student-driverless-cars-using-delaunay-triangulation/
贝塞尔曲线https://muzing.top/posts/6610880/
2、任务需求
在赛道进行路径规划,赛道两侧分别是红蓝锥桶,这里采用的参考资料2中的算法。
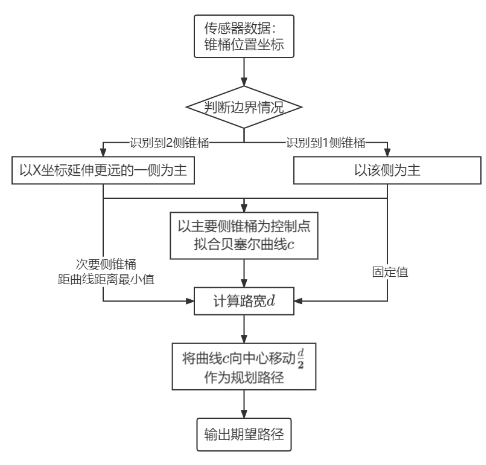
PanoSim仿真中采用「目标级雷达」,直接返回目标相对于自己的相对位置,但是相机下的位置不是真实世界下的位置
同样的我们也缺乏真实的路宽,在一侧没有的时候不能移动d/2
因此如果建立在拥有真实的坐标基础上,同时车身自带定位与建图的情况下,可以直接套用算法,目前采用的方案仅仅针对两侧都有锥桶,通过分别计算两侧贝塞尔曲线然后相加。
3、测试思路
原作者文档中解释非常清楚,这里仅仅做一些小小改动
3.1 贝塞尔曲线
red = get_traffic_cone_matrix(np.array(test_data[i]), 3) # 左侧锥桶位置矩阵blue = get_traffic_cone_matrix(np.array(test_data[i]), 2) # 右侧锥桶位置矩阵red_bezier = get_bezier_curve(red,25)blue_bezier = get_bezier_curve(blue, 25)#local_path = local_path_fitting(red, blue, translation_dis=1.5) # 规划出的局部路径矩阵# 左上角为原点plt.xlim(0, 1920)plt.ylim(0, 1080)plt.gca().invert_yaxis()plt.plot(red[:, 0], red[:, 1], "o-", color="r")plt.plot(blue[:, 0], blue[:, 1], "o-", color="b")#plt.plot(local_path[:, 1] * -1, local_path[:, 0], color="k", linestyle="--")x = (red_bezier + blue_bezier[::-1])/2这里采用了,左右两侧分别计算25个点的平均值,可以理解为中线。由于锥桶的顺序至关重要,原作者做了x方向排序,我们相加的取平均的的时候需要对一侧取反 x = (red_bezier + blue_bezier[::-1])/2,这样才能保证结果正确。
为了和原始图片保持一致,这里更改了画图原点,xy的方向。
3.2过滤点
没有采用原作者的fiter,因为相机存在畸变,实际测试中效果表现不好。因此自己尝试了两种方案。
3.2.1过滤置信度低的点
首先通过置信度进行筛选锥桶,可以看到原图的左边有很多蓝色锥桶,但是置信度低直接使用会影响结果。

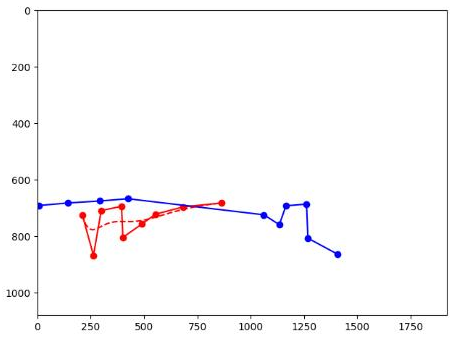
将上图的坐标点抽出来单独画图,可以看出这样是无法进行规划的。
这里对yolov5 detect.py做一点小改动,在write results的时候,原来是保存归一化后的结果符合yolo数据格式。我们虚妄同时保存锥桶框最下沿中点的位置,x1,y1,x2,y2是框的两个对角点。
xx=(x1+x2)/2
yy=max(y1,y2);
因此又新开了一个txt_path2的txt,保存我们需要的最下沿中点的x,y坐标。最后将保存的点放到作者的test_data.py下
# #Write resultsfor *xyxy, conf, cls in reversed(det):if save_txt: # Write to filexywh = (xyxy2xywh(torch.tensor(xyxy).view(1, 4)) / gn).view(-1).tolist() # normalized xywhline = (cls, *xywh, conf) if save_conf else (cls, *xywh) # label formatwith open(f'{txt_path}.txt', 'a') as f:f.write(('%g ' * len(line)).rstrip() % line + '\n')x1,y1,x2,y2 = xyxyxx=(x1+x2)/2yy=max(y1,y2);line2 = (cls,xx,yy)txt_path2 = txt_path + "_"with open(f'{txt_path2}.txt', 'a') as f2:f2.write(('%g ' * len(line2)).rstrip() % line2 + '\n')3.2.2过滤远的的点
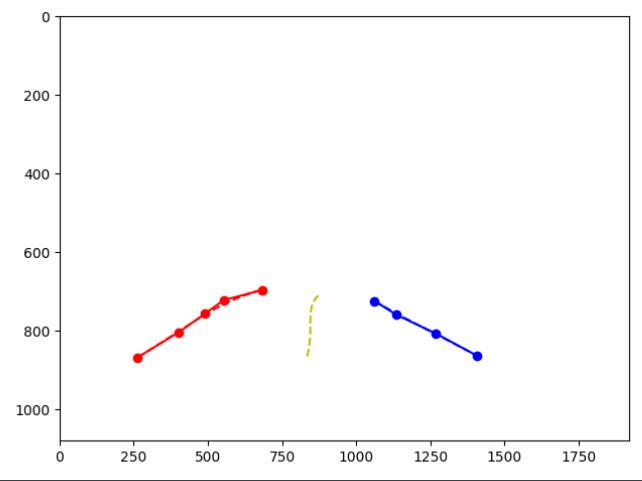
由于左边第一列红色实际上不是当前赛道,是U型弯回来的时候左侧锥桶,因此采用距离的方法,筛掉,当然这个距离目前是自己定的,因为看起来想个圆形,所以采用(960,1300)为圆心1400000为距离剔除远的点。
traffic_cone = traffic_cone[np.lexsort(traffic_cone[:, ::-1].T)] # 按x坐标排序cone= []for i in range(n):x=traffic_cone[i]xx=(x[0] - 960) ** 2 + (x[1] - 1600) ** 2if (x[0]-960)**2 + (x[1]-1300)**2 <= 1400000:cone.append(x)#clean_traffic_cone = filter_traffic_cone(traffic_cone) # 剔除异常的锥桶return np.array(cone)效果如下
4、实验结果
由于python画图不是16:9(1920,1080)的图像显示,因此通过ppt拉伸进行对比。ppt这个设置透明色会让路径多一些白点,只能凑活看一下。
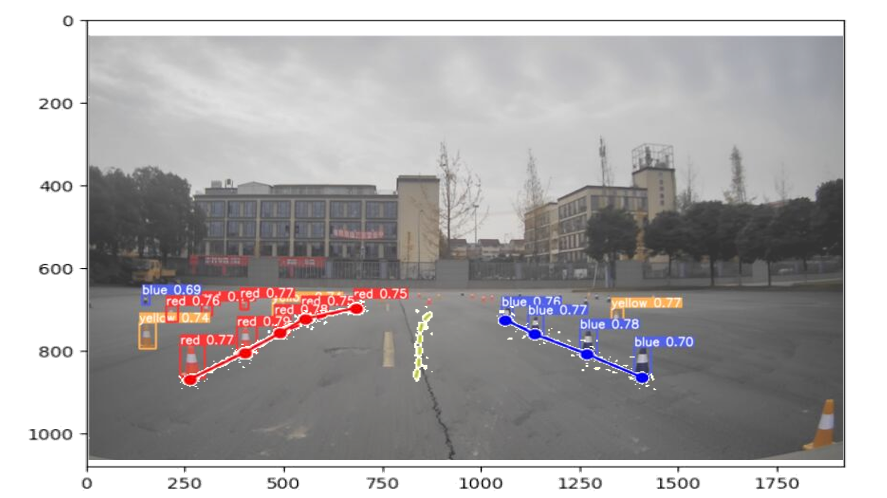
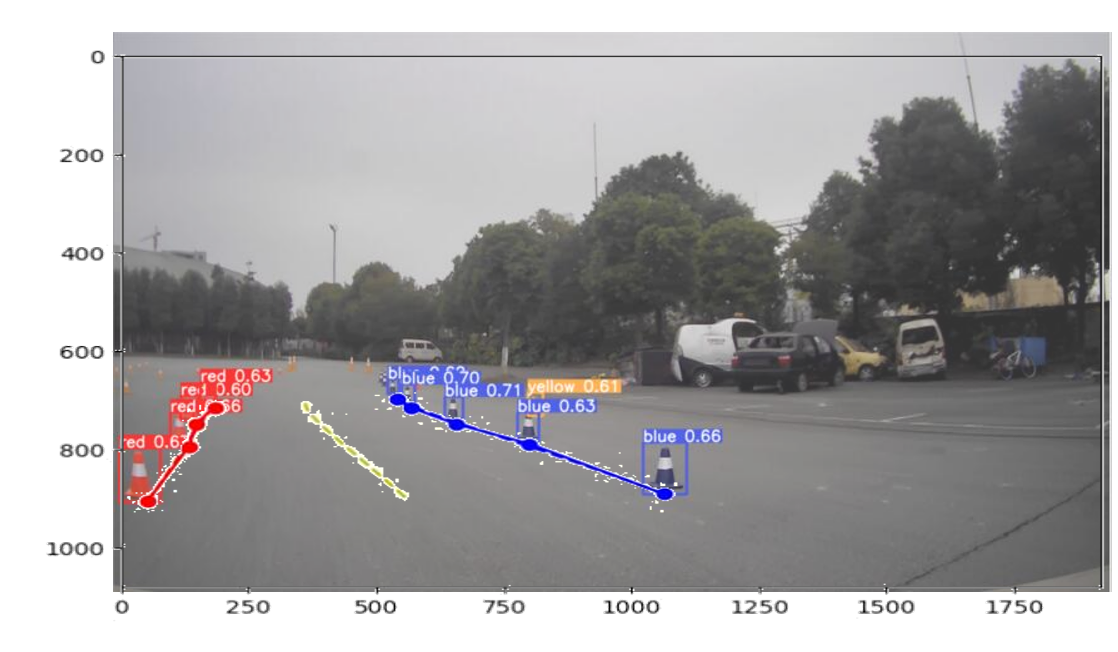
这里规划线明显在左侧,应该向左打方向~
5、存在问题
5.1当一侧没有的时候就不可以了,因为没有路宽,也不知道相机内参外参无法投影(留坑后期填)
解决方法:定位建图,丢失一侧主要发生在转弯过程,如果已经转完了证明之前早就观察到了,通过建图数据进行规划。
5.2 筛选点
目前的方案都比较粗糙,如果有实际点的位置和自身状态进行筛选更好,比如根据当前的转向预测个范围在筛选。
欢迎技术交流和探讨~
这篇关于(八)锥桶赛道路径规划的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





