本文主要是介绍【图神经网络论文阅读笔记:GCN-1】Spectral Networks and Locally Connected Networks on Graphs,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
【阅读笔记】Spectral Networks and Locally Connected Networks on Graphs
笔记目录
- 【阅读笔记】Spectral Networks and Locally Connected Networks on Graphs
- Abstract
- Background
- Spacial Construction
- Locality
- Multiresolution
- Deep Locally Connected Networks
- 小结
- Spectral Construction
- Harmonic Analysis on Weighted Graphs
- Extending Convolutions via the Laplacian Spectrum
- 术语
Abstract
本文是基于CNN(卷积神经网络,convolutional neural network)所构造的GCN。
本文提出两种构造,一种基于域的层次集群(a hierachical clustering of the domain),另一种是基于图拉普拉斯的谱(the spectrum of the graph Laplacian)。
其中后者(GCN-1)是本文的重点
结果显示,对于低维图,可以通过一些参数来学习卷积层,这些参数与输入大小无关。
Background
CNN在机器学习问题中非常成功,在这些问题中,底层数据表示的坐标具有网格(grid)结构(在1、2和3维),并且在这些坐标中要研究的数据具有相对于该网格的平移等变性/不变性(translational equivariance/invariance)。
同时,CNN相比传统的全连接网络(FC)还极大地减少了参数的使用。
然而,对于不具备较好几何结构的数据,传统的CNN不太适用。而图(graph)天然具备较好的表示能力。为了将卷积推广到图上,本文提出两种结构:spatial construction和spectral construction。
Spacial Construction
CNN 对一般图最直接的泛化是考虑多尺度(multiscale)、层次化(hierarchical)、局部感受野(local receptive field)。
网格(grid)将被带权图 G = ( Ω , W ) G=(\Omega ,W) G=(Ω,W)所替代—— Ω \Omega Ω是大小为 m m m的离散集,而 W W W是一个 m × m m\times m m×m的对称矩阵(元素非负)。
将 Ω \Omega Ω理解为节点集合, W W W理解为边矩阵
Locality
要在图中泛化局部(locality)的概念,可以通过权重 W W W来决定。定义“邻居”(neighborhood)的最直接方式是设定一个门限值 δ \delta δ,则节点 j j j的邻居(neighbor)为:
N δ ( j ) = { i ∈ Ω : W i j > δ } N_\delta(j)=\{i\in\Omega:W_{ij}>\delta\} Nδ(j)={i∈Ω:Wij>δ}
通过此处“邻居”的概念,之后会定义“社区”(neighborhood)
Multiresolution
由于网格具备天然的多尺度集群(multiscale clustering),CNN得以通过池化层和二次采样层(subsampling layer)减少网格的尺度。前人提出了多种在图上形成多尺度集群的方法。
本文使用一种简单的方法。下图说明了具有相应邻域的图的多分辨率集群(multiresolution clustering):
Deep Locally Connected Networks
spatial construction始于对图的多尺度集群。
考虑尺度为 K K K。设 Ω 0 = Ω \Omega_0=\Omega Ω0=Ω,对每个 k = 1... K k=1...K k=1...K,定义:
- Ω k \Omega_k Ωk为一个分割:将 Ω k − 1 \Omega_{k-1} Ωk−1分为 d k d_k dk个集群
- N k \mathcal{N}_k Nk为 Ω k − 1 \Omega_{k-1} Ωk−1中各元素所在的社区: N k = { N k , i ; i = 1... d k − 1 } \mathcal{N}_k=\{\mathcal{N}_{k,i};i=1...d_{k-1}\} Nk={Nk,i;i=1...dk−1}
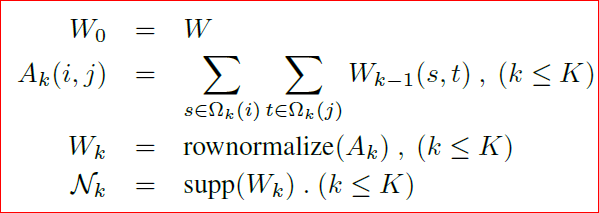
上图为无向图 G = ( Ω 0 , W ) G=(\Omega_0,W) G=(Ω0,W)的两级集群。
容易理解错误的是,这里的 W i j W_{ij} Wij不是“距离”,而是表征两个节点关系紧密与否的“权重”——关系越紧密,权值越大。
e.g. Ω 1 \Omega_1 Ω1是将 Ω 0 = Ω \Omega_0=\Omega Ω0=Ω分为 d 1 d_1 d1个集群; N 2 \mathcal{N}_2 N2是一个集合(共 d 1 d_1 d1个元素),其中每个元素都是 Ω 1 \Omega_1 Ω1中某个集群的“邻居”,即一个社区
图中:
- 灰色节点表示的是原始图 G G G中的各节点 Ω 0 \Omega_0 Ω0
- k = 1 k=1 k=1时划分第一级社区 Ω 1 \Omega_1 Ω1:每个彩色的多边形表示一个社区。各社区 N 1 j \mathcal{N}_{1j} N1j可以进一步用一个节点表示(图中彩色的节点)
- k = 2 k=2 k=2时划分第二级社区 Ω 2 \Omega_2 Ω2:椭圆圈表示在上一步基础之上划分的各社区 N 2 j \mathcal{N}_{2j} N2j
据此定义网络的第 k k k层(k-th layer of the network):不失一般性地,假设输入信号是在 Ω 0 \Omega_0 Ω0中定义的实信号(real signal),用 f k f_k fk表示在第 k k k层中创建的filters的数量。在网络的每一层,会把用 Ω k − 1 \Omega_{k-1} Ωk−1索引(index)的 f k − 1 f_{k-1} fk−1维信号转化为用 Ω k \Omega_{k} Ωk索引的 f k f_{k} fk维信号,从而权衡空间分辨率(spatial resolution)与新创建的特征坐标(feature coordinates)。
通俗地说,就是每一层都使得空间分辨率有所降低、“图”更加“抽象”,但图中隐含的信息通过特征的提取变得更加明显。
更正式地,如果第 k k k层的输入是 d k − 1 × f k − 1 d_{k-1}\times f_{k-1} dk−1×fk−1的 x k = ( x k , i ; i = 1... f k − 1 ) x_k=(x_{k,i};i=1...f_{k-1}) xk=(xk,i;i=1...fk−1),则输出 x k + 1 x_{k+1} xk+1为:
x k + 1 , j = L k h ( ∑ i = 1 f k − 1 F k , i , j x k , i ) ( j = 1... f k ) (2.1) x_{k+1,j}=L_kh(\sum_{i=1}^{f_{k-1}}F_{k,i,j}x_{k,i})\quad(j=1...f_k) \tag{2.1} xk+1,j=Lkh(i=1∑fk−1Fk,i,jxk,i)(j=1...fk)(2.1)
其中 F k , i , j F_{k,i,j} Fk,i,j是 d k − 1 × d k − 1 d_{k-1}\times d_{k-1} dk−1×dk−1大小的稀疏矩阵,且在由 N k \mathcal{N}_k Nk所给出的位置上,其元素(entries)是非零的。 L k L_k Lk是在 Ω k \Omega_k Ωk中的每个集群上做池化操作的输出结果。如下图所示。
可以理解为:
初始值 d 0 = ∣ Ω 0 ∣ d_0=|\Omega_0 | d0=∣Ω0∣即原图 G G G中节点的数目, f 0 = 1 f_0=1 f0=1
x k + 1 x_{k+1} xk+1是 x k x_k xk经过第 k k k层的 f k f_k fk个filter作用后得到的结果
h h h为激活函数注:“entries”
The individual items in an m×n matrix A, often denoted by ai,j, where i and j usually vary from 1 to m and n, respectively, are called its elements or entries.
矩阵中的元素可以叫elements,items,或者entries。
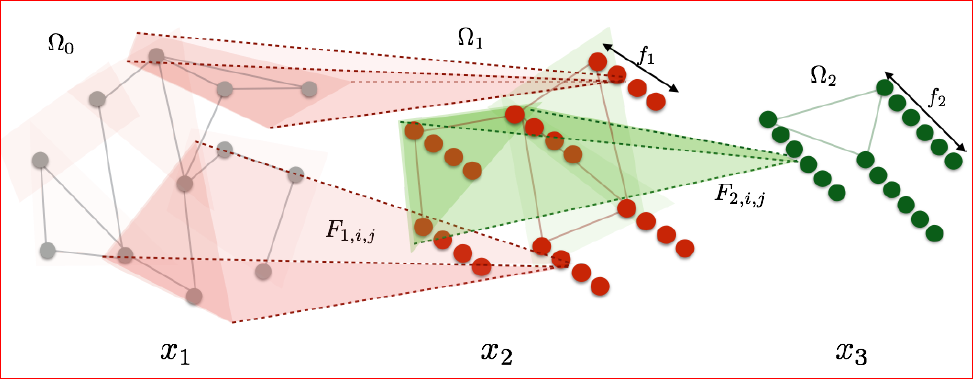
上图为 K = 2 K=2 K=2情况下, ( 2.1 ) (2.1) (2.1)式所描述的空间构造,其中池化操作为演示方便而隐含在了过滤阶段(filtering stage)。每一个转化层都会损失空间分辨率,但也会增加filters的数量。
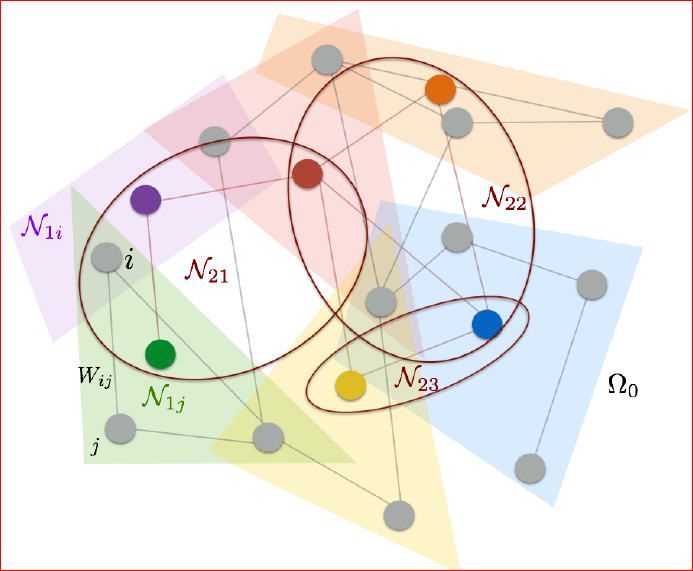
本文使用如下方式构造 Ω k \Omega_k Ωk和 N k \mathcal{N}_k Nk:
小结
空间构造可能看起来很幼稚,但它的优点是它需要对图进行相对较弱的正则性假设。 具有低内在维度的图具有局部邻域,即使不存在良好的全局嵌入也是如此。 然而,在这种结构下,没有简单的方法可以在图形的不同位置之间进行权重共享。 一种可能的选择是考虑将图形全局嵌入到低维空间中,这在高维数据的实践中很少见。
Spectral Construction
图的全局结构可以利用其图拉普拉斯算子(graph-Laplacian)的谱(spectrum)来推广卷积运算符。
Harmonic Analysis on Weighted Graphs
harmonic analysis: analysis of a periodic function into a sum of simple sinusoidal components.
synonymous: Fourier analysis
组合拉普拉斯矩阵(combinatorial Laplacian) L = D − W L=D-W L=D−W或图拉普拉斯矩阵(graph Laplacian) L = I − D − 1 / 2 W D − 1 / 2 \mathcal{L}=I-D^{-1/2}WD^{-1/2} L=I−D−1/2WD−1/2是对网格中的拉普拉斯算子的推广。
L L L:图拉普拉斯矩阵,就是图上的拉普拉斯算子 Δ \Delta Δ
D D D:度矩阵
W W W:权重矩阵图拉普拉斯算子 Δ \Delta Δ作用在由图节点信息构成的向量 f ⃗ \vec{f} f上,得到的结果等于图拉普拉斯矩阵 L L L和向量 f ⃗ \vec{f} f的点积:
Δ f ⃗ = L f ⃗ , f ⃗ = ( f 1 , . . . f N ) \Delta\vec{f}=L\vec{f},\qquad \vec{f}=(f_1,...f_N) Δf=Lf,f=(f1,...fN)
设 x x x是 m m m维的向量,节点 i i i的平滑度(smoothness)可定义为:
∥ ▽ x ∥ W 2 ( i ) = ∑ j W i j [ x ( i ) − x ( j ) ] 2 \|\triangledown x\|_W^2(i)=\sum_j W_{ij}[x(i)-x(j)]^2 ∥▽x∥W2(i)=j∑Wij[x(i)−x(j)]2
Extending Convolutions via the Laplacian Spectrum
设 W W W是一个带权图, Ω \Omega Ω表示索引集。设 V V V是拉普拉斯矩阵 L L L的各特征向量(eigenvector)组成的列向量矩阵,按特征值(eigenvalue)排序。可以据此在图上做卷积网络的推广。
x k + 1 , j = h ( V ∑ i = 1 f k − 1 F k , i , j V T x k , i ) ( j = 1... f k ) x_{k+1,j}=h(V\sum_{i=1}^{f_{k-1}}F_{k,i,j}V^Tx_{k,i})\quad(j=1...f_k) xk+1,j=h(Vi=1∑fk−1Fk,i,jVTxk,i)(j=1...fk)
f k f_k fk为第 k k k层中创建的filters的数量
每层 k = 1... K k=1...K k=1...K中,将大小为 ∣ Ω ∣ × f k − 1 |\Omega|\times f_{k-1} ∣Ω∣×fk−1的输入向量 x k x_k xk,转化为大小为 ∣ Ω ∣ × f k |\Omega|\times f_{k} ∣Ω∣×fk的输出向量 x k + 1 x_{k+1} xk+1
F k , i , j F_{k,i,j} Fk,i,j是一个对角矩阵(即为要学习的参数——卷积核)
h h h为激活函数理论上,每层需要 ∣ Ω ∣ × f k − 1 × f k |\Omega|\times f_{k-1}\times f_k ∣Ω∣×fk−1×fk个参数:
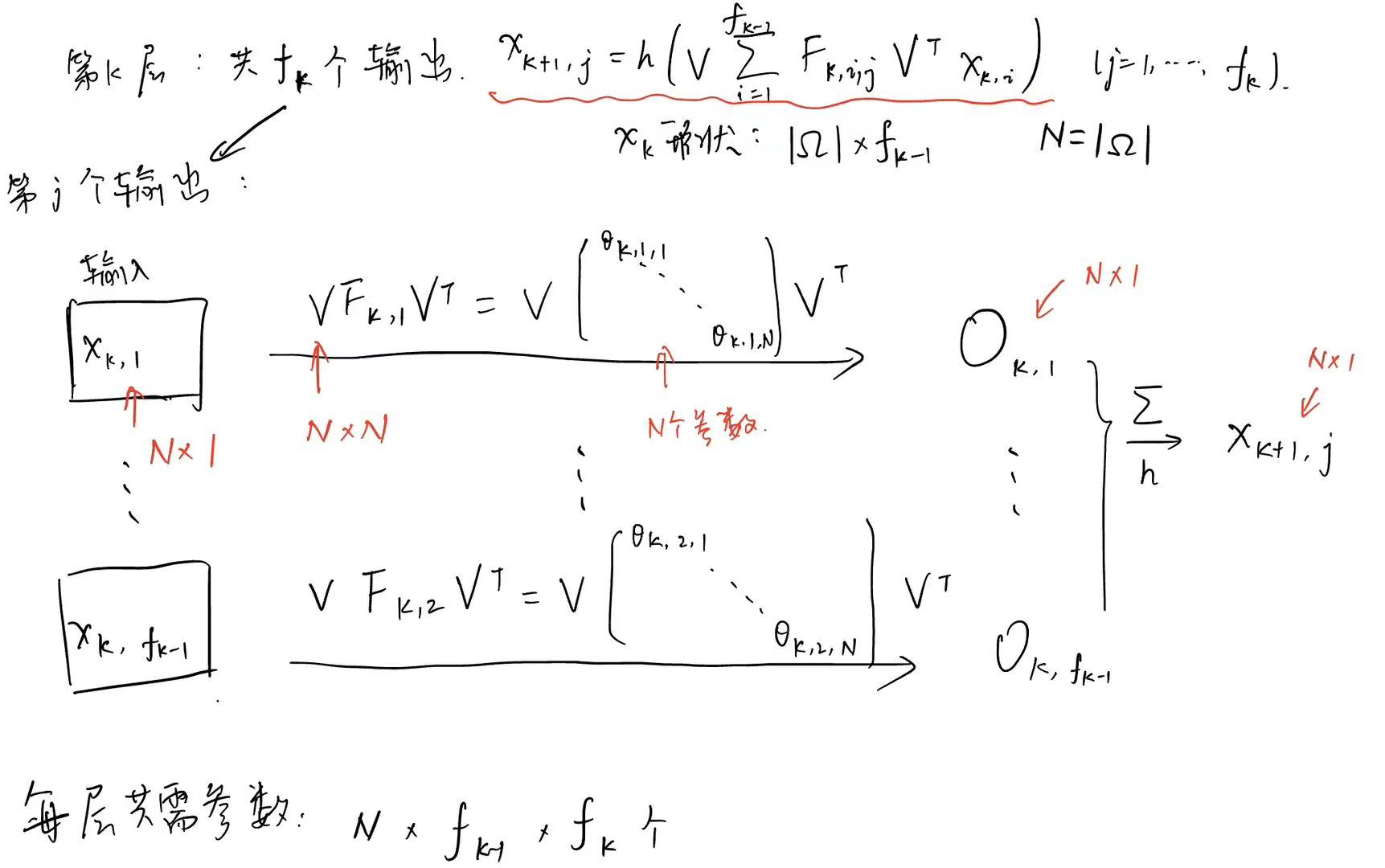
通常来说,只有拉普拉斯算子的前 d d d个特征向量是有用的,因此可以将特征向量组成的列矩阵 V V V变为 V d V_d Vd。这样每层需要训练的参数减少到 d ⋅ f k − 1 ⋅ f k = O ( ∣ Ω ∣ ) d\cdot f_{k-1}\cdot f_k=O(|\Omega|) d⋅fk−1⋅fk=O(∣Ω∣)。
术语
multiscale clustering:多尺度集群
multiresolution clustering:多分辨率集群
spatial resolution:空间分辨率
neighbor:邻居
neighborhood:社区
spectrum:谱
Laplacian:拉普拉斯算子
eigenvector/eigenvalue:特征向量/特征值
这篇关于【图神经网络论文阅读笔记:GCN-1】Spectral Networks and Locally Connected Networks on Graphs的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








