RTKLIB源码阅读（二）时间系统、坐标系统

原始 Markdown文档、Visio流程图、XMind思维导图见：https://github.com/LiZhengXiao99/Navigation-Learning

 一、时间系统

double  str2num(const char *s, int i, int n);
int     str2time(const char *s, int i, int n, gtime_t *t);
void    time2str(gtime_t t, char *str, int n);
gtime_t epoch2time(const double *ep);
void    time2epoch(gtime_t t, double *ep);
gtime_t gpst2time(int week, double sec);
double  time2gpst(gtime_t t, int *week);
gtime_t gst2time(int week, double sec);
double  time2gst(gtime_t t, int *week);
gtime_t bdt2time(int week, double sec);
double  time2bdt(gtime_t t, int *week);
char    *time_str(gtime_t t, int n);gtime_t timeadd  (gtime_t t, double sec);
double  timediff (gtime_t t1, gtime_t t2);
gtime_t gpst2utc (gtime_t t);
gtime_t utc2gpst (gtime_t t);
gtime_t gpst2bdt (gtime_t t);
gtime_t bdt2gpst (gtime_t t);
gtime_t timeget  (void);
void    timeset  (gtime_t t);
void    timereset(void);
double  time2doy (gtime_t t);
double  utc2gmst (gtime_t t, double ut1_utc);
int read_leaps(const char *file);int adjgpsweek(int week);
uint32_t tickget(void);
void sleepms(int ms);

时间系统的一些基础知识，各种书上都有，也可以看这篇 博客，我在此就不写那么细了，重点讲一讲RTKLIB涉及到的，相关的结构体、函数

1、时间系统基本概念

时间系统：时间起点基准+时间间隔尺度

1. 恒星时（Sidereal Time，ST）：以春分点为基本参考点，由春分点周日视运动确定的时间称为恒星时。

1. 真太阳时：以真太阳作为基本参考点，由其周日视运动确定的时间称为真太阳时。

1. 平太阳时：（由于真太阳的视运动是不均匀的，所以引入虚拟的在赤道上匀速运行的平太阳，其速度等于真太阳周年运动的平均速度），平太阳连续经过同一子午圈的时间称为一个平太阳日，分为24个平太阳时。

1. 历书时（Ephemeris Time，ET）：以地球公转为基准的度量时间的系统。（秒长规定：1900年1月1日12时整回归年长度的 1/31556925.9747；起始历元定在1900年1月1日12时）太阳系质心力学时TDB，地球质心力学时TDT。

1. 原子时（Atomic Time，AT）：是一种以原子谐振信号周期为标准，并对它进行连续计数的时标。

UTC。各种GNSS时、TT都是建立在原子时基础上，只是起点的选择、是否跳秒、时间系统的维持方式不同。

1. 国际原子时（International Atomic Time，TAI）：由各实验室的原子钟维持。取 1958 年 1 月 1 日 0 时 0 分 0 秒世界时(UT)的瞬间作为同年同月同日 0 时 0 分 0 秒TAI。（事后发现，在该瞬间原子时与世界时的时刻之差为0.0039秒。这一差值就作为历史事实而保留下来。）

1. 区时：全球化为24个时区，在同一时区采用该时区中央子午线上的平太阳时为区时。

1. 世界时UT：0区的区时，即格林尼治起始子午线上的平太阳时为世界时UT

• UT0：直接天文观测的世界时

• UT1：经过极移改正的世界时

• UT2：再经过地球自转速度季节性改正的世界时

1. 协调世界时（Universal Time of Coordination，UTC）：以原子秒长为计量单位，在时刻上与平太阳时之差小于 0.9 秒的时间系统。UT1+跳秒。

C语言获取的系统时间时UTC

1. 跳秒：leap second，在 1980 年 1 月 6 日 0 时 GPS 时与 UTC 时对齐，GPS 时是依靠稳定的原子钟来维持的，也就是说它的单位时间长度是很稳定的；而协调世界时是根据天文确定的，和地球自转有关，但是地球自转速度在不断变慢，也就是说协调世界时的单位时间长度并不是恒定的。但是总不能他们稍微不一致就调吧，这样也太麻烦了，所以就规定，当两者相差接近1秒时，就让UTC跳一秒。可看官网。

rtkcmn.c中也有跳秒的定义

static double leaps[MAXLEAPS+1][7]={ /* (y,m,d,h,m,s,utc-gpst) */{2017,1,1,0,0,0,-18},{2015,7,1,0,0,0,-17},{2012,7,1,0,0,0,-16},{2009,1,1,0,0,0,-15},{2006,1,1,0,0,0,-14},{1999,1,1,0,0,0,-13},{1997,7,1,0,0,0,-12},{1996,1,1,0,0,0,-11},{1994,7,1,0,0,0,-10},{1993,7,1,0,0,0, -9},{1992,7,1,0,0,0, -8},{1991,1,1,0,0,0, -7},{1990,1,1,0,0,0, -6},{1988,1,1,0,0,0, -5},{1985,7,1,0,0,0, -4},{1983,7,1,0,0,0, -3},{1982,7,1,0,0,0, -2},{1981,7,1,0,0,0, -1},{0}
};

1. GPS 时（GPS Time，GPST）：由 GPS 星载原子钟和地面监控站原子钟组成的一种原子时基准，与国际原子时保持有 19s 的常数差，并在 GPS 标准历元 1980 年 1 月 6 日 0 时与 UTC 保持一致。

GPS系统内部所采用的时间系统是GPS时，其时间零点定义为1980年1月5日 夜与1980年1月6日晨之间的子夜。GPS时系统在标示时间时所采用的最大时间单 位为周（week，604800秒），其标示时间的方法是从1980年1月 6日0时开始起算 的周数（WN-Week Number）加上被 称为周内时间（TOW-Time of Week）的从 每周周六/周日子夜开始起算的秒数。
例如：“1980年1月6日0时0分0秒”用GPS时标示法则为“第0周0秒”；而 “2004年5月1日10时5分15秒”用GPS时标示法则为“第1268周第554715秒”。 在GPS卫星所发送的导航电文中，时间信息的标示就是采用这种形式。

1. 北斗时（BDS Time，BDT） ：同 GPST 一样由原子钟保持基准，在 2006 年 1 月 1 日 0 时与 UTC 保持一致。因为从 1980 年到 2006 年共有 14 次跳秒发生，所以 BDT 和 GPST 相差 14 秒且基本恒定不变。

1. GLONASS时（GLONASS Time，GLST）：以莫斯科本地协调时 UCTsu 定义，其值与 UTC 存在 3 小时时差。

1. Galileo时（Galileo Time，GST）：同 GPST 保持一致。

1. QZSSS时 (QZSS TIME , QZSST) ：同 GPST 保持一致。

1. 判断闰年：年份是 4 的倍数但不是 100 的倍数或者年份是 400 的倍数。

1. GPS 周：（GPS Week，GPSW） GPS系统内部描述时间的一种方式，它的起点为 1980 年 1 月 5 日夜晚与 1980 年 1 月 6 日凌晨之间 0 点（这天是周日，老外经常周日表示一周的第一天，以0表示）。

rtkcmn.c中有GPST(GST)、GLST、BDT的时间基准的的定义

static const double gpst0[]={1980,1, 6,0,0,0}; /* gps time reference */
static const double gst0 []={1999,8,22,0,0,0}; /* galileo system time reference */
static const double bdt0 []={2006,1, 1,0,0,0}; /* beidou time reference */

1. 儒略日：（Julian Day，JD） 是指由公元前 4713 年 1 月 1 日，协调世界时中午 12 时开始所经过的天数。采用连续的数值来标示时间，适合科学计算，且可以很方便地将采用不同方法所标示的时间联系起来，但无法直接反映季节等信息，故日常生活中不常用。

1. 简化儒列日：（Modified Julian Day、MJD），由于儒略时的计时起点距今较为久远，若将现今时间用儒略时来表示，数值 非常大。1973年国际天文学联合会提出 了约化儒略日的时间标示法，其起点是 1858 年 11 月 17 日世界时 0 时。MJD = JD - 2400000.5

1. 年积日：（Day Of Year，DOY） 一年当中的第几天，其取值范围为[1,365]，

在GPS中的用途：年积日通常用来区分观测时段，常用于GPS观测文件 的 命名。例如，在RINEX格式中就规定：在数据文件的8字符主文件名中，第5-7个字符为观测起始时刻的年积日。

1. 天内秒：（Second Of Day，SOD） 一天中的第几秒，其取值范围为[1,86400]

1. 周内秒：（Second Of Week，SOW） 一周中的第几秒，其取值范围为[1,604800]

1. 周内分：(Hour Of Week，HOW) 一周中的第几小时，其取值范围为[1,168]

2、RTKLIB时间的表示、转换、处理

1. gtime_t结构体：GNSS数据处理对时间精度非常敏感，如果用double类型的TOW，相当于距离上只有0.004m的精度，。出于精度的考虑，RTKLIB将时间表示为gtime_t结构体，用time_t类型表示1970年以来的整秒数，有double类型表示不到1s的时间，time_t随机器而定一般是是无符号__int64 类型，由于整数长度限制，gtime_t不能表示1970年以前和2038以后的时间。

gtime_t只是一种时间表示的形式，来表示GPST、UCT、BDT、GST

typedef struct {        /* time struct */time_t time;        /* time (s) expressed by standard time_t */double sec;         /* fraction of second under 1 s */
} gtime_t;

1. RTKLIB处理gtime_t的函数，在rtkcmn.c中

• str2num () :字符串转数字

RTKLIB中的字符转换数字的函数str2num中有一个特殊的地方，对字符多进行了一步判断，判断其是否为字符’d’或’D’,若符合则将其转换为’E’，其余则不变，进行这一步的目的在于对采用科学计数法表示的数字的判读。C语言中用E表示的科学计数法数字可以识别，而D不能，因此在此处进行转换。

extern double str2num(const char *s, int i, int n)
{double value;char str[256],*p=str;if (i<0||(int)strlen(s)<i||(int)sizeof(str)-1<n) return 0.0;for (s+=i;*s&&--n>=0;s++) *p++=*s=='d'||*s=='D'?'E':*s;*p='\0';return sscanf(str,"%lf",&value)==1?value:0.0;
}

• str2time ()：字符串转gtime_t，string格式： ("... yyyy mm dd hh mm ss ...")

extern int str2time(const char *s, int i, int n, gtime_t *t)
{double ep[6];   //ep数组表示时间：double类型数组，存年月日时分秒char str[256],*p=str;if (i<0||(int)strlen(s)<i||(int)sizeof(str)-1<i) return -1;for (s+=i;*s&&--n>=0;) *p++=*s++;*p='\0';if (sscanf(str,"%lf %lf %lf %lf %lf %lf",ep,ep+1,ep+2,ep+3,ep+4,ep+5)<6)return -1;  //sscanf从字符串中读取年月日时分秒，先存到ep数组中if (ep[0]<100.0) ep[0]+=ep[0]<80.0?2000.0:1900.0;*t=epoch2time(ep);  //再把ep数组转换成gtime_t类型return 0;
}

• epoch2time ()：把epoch时间数组转为gtime_t

格里高利至儒略日转换方法：
JD=floor(365.25*(y+4716))+floor(30.6001*(m+1))+D+h/24-1537.5
若m≤2,则 y=Y-1，m=M+12；
若m＞2,则 y=Y, m=M。
式中：JD为儒略日；Y为年：M为月；D为日；h=H+Min/60+s/3600,H,Min和S分别为时，分和秒；floor()为取整函数，有floor(a) ≤a，例如floor(-2.3)=-3。

extern gtime_t epoch2time(const double *ep)
{const int doy[]={1,32,60,91,121,152,182,213,244,274,305,335};   //每月第一天的doygtime_t time={0};int days,sec,year=(int)ep[0],mon=(int)ep[1],day=(int)ep[2];if (year<1970||2099<year||mon<1||12<mon) return time;/* leap year if year%4==0 in 1901-2099 */days=(year-1970)*365+(year-1969)/4+doy[mon-1]+day-2+(year%4==0&&mon>=3?1:0);sec=(int)floor(ep[5]);time.time=(time_t)days*86400+(int)ep[3]*3600+(int)ep[4]*60+sec;time.sec=ep[5]-sec;return time;
}

• time2epoch ()：把gtime_t转为epoch时间数组

儒略日至格里高利转换方法：
a= floor(julday+0.5);
b=a+1537;
c = floor((b-122.1)/365.25);
d = floor(365.25*c);
e = floor((b-d)/30.6001);
D = floor(b-d- floor(30.6001*e)+ rem(julday+.5,1))； 	%天
H=(rem(julday+.5,1))*24;  								%时
M=e-1-12*floor(e/14); 									%月
Y=c-4715-floor((7+M)/10); 								%年
Rem 函数是取余函数 rem(x,y)=x-y*fix(x/y),其中fix()是向0取整，例如fix(-1.5)=-1, fix(1.5)=1。
注：上面的转换算法仅在1900年3月1日至2100年2月28日期间有效。

extern void time2epoch(gtime_t t, double *ep)
{const int mday[]={ /* # of days in a month */31,28,31,30,31,30,31,31,30,31,30,31,31,28,31,30,31,30,31,31,30,31,30,31,31,29,31,30,31,30,31,31,30,31,30,31,31,28,31,30,31,30,31,31,30,31,30,31};int days,sec,mon,day;/* leap year if year%4==0 in 1901-2099 */days=(int)(t.time/86400);sec=(int)(t.time-(time_t)days*86400);for (day=days%1461,mon=0;mon<48;mon++) {if (day>=mday[mon]) day-=mday[mon]; else break;}ep[0]=1970+days/1461*4+mon/12; ep[1]=mon%12+1; ep[2]=day+1;ep[3]=sec/3600; ep[4]=sec%3600/60; ep[5]=sec%60+t.sec;
}

• time2str()：gtime_t转字符串，格式：string ("yyyy/mm/dd hh:mm:ss.ssss") ，以传入的字符串指针s返回。

• n：小数位数（0~12），前面的年月日时分一定有，

• n取0，输出格式：yyyy/mm/dd hh:mm:ss

• n>0，yyyy/mm/dd hh:mm:ss后面还有n位

extern void time2str(gtime_t t, char *s, int n)
{double ep[6];if (n<0) n=0; else if (n>12) n=12;if (1.0-t.sec<0.5/pow(10.0,n)) {t.time++; t.sec=0.0;};time2epoch(t,ep);	//先把时间转为epoch时间数组sprintf(s,"%04.0f/%02.0f/%02.0f %02.0f:%02.0f:%0*.*f",ep[0],ep[1],ep[2],ep[3],ep[4],n<=0?2:n+3,n<=0?0:n,ep[5]);
}

• time_str()：gtime_t转字符串，类time2str()，区别是转出的字符串直接做返回值，返回的是静态内存的首地址，所以不要乱释放或者使用 。

extern char *time_str(gtime_t t, int n)
{static char buff[64];time2str(t,buff,n);return buff;
}

• time2doy ()：gtime_t转年积日DOY。

extern double time2doy(gtime_t t)
{double ep[6];time2epoch(t,ep);ep[1]=ep[2]=1.0; ep[3]=ep[4]=ep[5]=0.0;return timediff(t,epoch2time(ep))/86400.0+1.0;
}

• timeadd()：给传入的gtime_t增加秒数

extern gtime_t timeadd(gtime_t t, double sec)
{double tt;t.sec+=sec; tt=floor(t.sec); t.time+=(int)tt; t.sec-=tt;return t;
}

• timediff ()：求时间差 t1 - t2

extern double timediff(gtime_t t1, gtime_t t2)
{return difftime(t1.time,t2.time)+t1.sec-t2.sec;
}

• timeget(): 获取系统UTC时间，表示成gtime_t

• getimeofday()：获取到的是自1970-01-01 00:00:00 +0000 (UTC)以来的秒数和微秒数，原型：int gettimeofday(struct timeval *tv, struct timezone *tz);

struct timeval {	//tvtime_t      tv_sec;     /* seconds */suseconds_t tv_usec;    /* microseconds */
};struct timezone {	//tz 是一个过时的设计，填NULL即可int tz_minuteswest;     /* minutes west of Greenwich */int tz_dsttime;         /* type of DST correction */
};

• gmtime()：将time_t转换为可读的UTC时间格式用gmtime函数

• GetSystemTime()：获取系统UTC时间。

typedef struct _SYSTEMTIME {WORD wYear;WORD wMonth;WORD wDayOfWeek;WORD wDay;WORD wHour;WORD wMinute;WORD wSecond;WORD wMilliseconds;
} SYSTEMTIME, *PSYSTEMTIME, *LPSYSTEMTIME;

static double timeoffset_=0.0;        /* time offset (s) */extern gtime_t timeget(void)
{gtime_t time;double ep[6]={0};
#ifdef WIN32SYSTEMTIME ts;GetSystemTime(&ts); /* utc */ep[0]=ts.wYear; ep[1]=ts.wMonth;  ep[2]=ts.wDay;ep[3]=ts.wHour; ep[4]=ts.wMinute; ep[5]=ts.wSecond+ts.wMilliseconds*1E-3;
#elsestruct timeval tv;struct tm *tt;if (!gettimeofday(&tv,NULL)&&(tt=gmtime(&tv.tv_sec))) {ep[0]=tt->tm_year+1900; ep[1]=tt->tm_mon+1; ep[2]=tt->tm_mday;ep[3]=tt->tm_hour; ep[4]=tt->tm_min; ep[5]=tt->tm_sec+tv.tv_usec*1E-6;}
#endiftime=epoch2time(ep);#ifdef CPUTIME_IN_GPST /* cputime operated in gpst */time=gpst2utc(time);
#endifreturn timeadd(time,timeoffset_);
}

• timeset()：设置相对于UTC的时间偏移，只对**timeget()**有影响。

extern void timeset(gtime_t t)
{timeoffset_+=timediff(t,timeget());
}

• timereset()：时间偏移重置为0.0。

extern void timereset(void)
{timeoffset_=0.0;
}

• time2sec()：由gtime_t算SOD和0时0分0秒的gtime_t

static double time2sec(gtime_t time, gtime_t *day)
{double ep[6],sec;time2epoch(time,ep);    //gtime_t转epoch时间数组sec=ep[3]*3600.0+ep[4]*60.0+ep[5];  //根据时分秒算天内秒SODep[3]=ep[4]=ep[5]=0.0;  //时分秒赋值0*day=epoch2time(ep);    //0时0分0秒的gtime_treturn sec;
}

• utc2gmst()：UTC转格林威治平均恒星时，返回弧度

extern double utc2gmst(gtime_t t, double ut1_utc)
{const double ep2000[]={2000,1,1,12,0,0};gtime_t tut,tut0;double ut,t1,t2,t3,gmst0,gmst;tut=timeadd(t,ut1_utc);ut=time2sec(tut,&tut0);t1=timediff(tut0,epoch2time(ep2000))/86400.0/36525.0;t2=t1*t1; t3=t2*t1;gmst0=24110.54841+8640184.812866*t1+0.093104*t2-6.2E-6*t3;gmst=gmst0+1.002737909350795*ut;return fmod(gmst,86400.0)*PI/43200.0; /* 0 <= gmst <= 2*PI */
}

• adjgpsweek():用CPU时间调整GPS周

extern int adjgpsweek(int week)
{int w;(void)time2gpst(utc2gpst(timeget()),&w);	//从CPU获取周数if (w<1560) w=1560; /* use 2009/12/1 if time is earlier than 2009/12/1 */return week+(w-week+1)/1024*1024;	//转为GPS周，并返回
}

• tickget()：

• timeGetTime() ：返回以 毫秒 计的系统时间。该时间为从系统开启算起所经过的时间

extern uint32_t tickget(void)
{
#ifdef WIN32return (uint32_t)timeGetTime();
#elsestruct timespec tp={0};struct timeval  tv={0};#ifdef CLOCK_MONOTONIC_RAW/* linux kernel > 2.6.28 */if (!clock_gettime(CLOCK_MONOTONIC_RAW,&tp)) {return tp.tv_sec*1000u+tp.tv_nsec/1000000u;}else {gettimeofday(&tv,NULL);return tv.tv_sec*1000u+tv.tv_usec/1000u;}
#elsegettimeofday(&tv,NULL);return tv.tv_sec*1000u+tv.tv_usec/1000u;
#endif
#endif /* WIN32 */
}

• sleepms()：线程挂起若干毫秒

extern void sleepms(int ms)
{
#ifdef WIN32if (ms<5) Sleep(1); else Sleep(ms);
#elsestruct timespec ts;if (ms<=0) return;ts.tv_sec=(time_t)(ms/1000);ts.tv_nsec=(long)(ms%1000*1000000);nanosleep(&ts,NULL);
#endif
}

1. gtime_t、GPST、UCT、BDT、GST间的转换函数

RTKLIB内以GPST进行计算处理，其它时间系统的数据需转换为GPST数据才能进行计算。
gtime_t只是一种时间表示的形式，来表示GPST、UCT、BDT、GST

• gpst2time ()：GPST转gtime_t。

time2gpst ()：gtime_t转GPST。

• WN：以第二个参数int指针week返回

• TOW：double类型返回值

extern double time2gpst(gtime_t t, int *week)
{gtime_t t0=epoch2time(gpst0);time_t sec=t.time-t0.time;int w=(int)(sec/(86400*7));if (week) *week=w;return (double)(sec-(double)w*86400*7)+t.sec;
}

extern gtime_t gpst2time(int week, double sec)
{gtime_t t=epoch2time(gpst0);if (sec<-1E9||1E9<sec) sec=0.0;t.time+=(time_t)86400*7*week+(int)sec;t.sec=sec-(int)sec;return t;
}

• gpst2time ()：GST转gtime_t。

time2gst ()：gtime_t转GST。

• WN：以第二个参数int指针week返回

• TOW：double类型返回值

extern double time2gst(gtime_t t, int *week)
{gtime_t t0=epoch2time(gst0);time_t sec=t.time-t0.time;int w=(int)(sec/(86400*7));if (week) *week=w;return (double)(sec-(double)w*86400*7)+t.sec;
}

extern gtime_t gst2time(int week, double sec)
{gtime_t t=epoch2time(gst0);if (sec<-1E9||1E9<sec) sec=0.0;t.time+=(time_t)86400*7*week+(int)sec;t.sec=sec-(int)sec;return t;
}

• bdt2time ()：BDT转gtime_t。

• time2bdt ()：gtime_t转BDT。

• WN：以第二个参数int指针week返回

• TOW：double类型返回值

extern double time2bdt(gtime_t t, int *week)
{gtime_t t0=epoch2time(bdt0);time_t sec=t.time-t0.time;int w=(int)(sec/(86400*7));if (week) *week=w;return (double)(sec-(double)w*86400*7)+t.sec;
}

extern gtime_t bdt2time(int week, double sec)
{gtime_t t=epoch2time(bdt0);if (sec<-1E9||1E9<sec) sec=0.0;t.time+=(time_t)86400*7*week+(int)sec;t.sec=sec-(int)sec;return t;
}

• gpst2utc()：GPST转UTC，跳秒

utc2gpst ()：UTC转GPST

extern gtime_t utc2gpst(gtime_t t)
{int i;for (i=0;leaps[i][0]>0;i++) {if (timediff(t,epoch2time(leaps[i]))>=0.0) return timeadd(t,-leaps[i][6]);}return t;
}

extern gtime_t gpst2utc(gtime_t t)
{gtime_t tu;int i;for (i=0;leaps[i][0]>0;i++) {tu=timeadd(t,leaps[i][6]);if (timediff(tu,epoch2time(leaps[i]))>=0.0) return tu;}return t;
}

3、跳秒相关函数

（1）为了保证导航和定位精度，全球定位系统GPS建立了专门的时间系统———GPS系统时，简称GPST。
（2）GPST属原子时系统，其秒长为国际制秒（SI），与原子时相同，但其起点与国际原子时（IAT）不同。因此GPST与IAT之间存在一个常数差，它们的关系为：
IAT – GPST = 19s
（3）GPST与UTC规定于1980年1月1日0时相一致,其后随着时间成整数倍积累, 至2017年底该差值为18s。GPST由主控站原子钟控制。
GPST = UTC(USNO) + ΔtUTC
ΔtUTC为GPST和UTC之间的闰秒差，在GPS导航电文中播发。

static double leaps[MAXLEAPS+1][7]={ /* leap seconds (y,m,d,h,m,s,utc-gpst) */{2017,1,1,0,0,0,-18},{2015,7,1,0,0,0,-17},{2012,7,1,0,0,0,-16},{2009,1,1,0,0,0,-15},{2006,1,1,0,0,0,-14},{1999,1,1,0,0,0,-13},{1997,7,1,0,0,0,-12},{1996,1,1,0,0,0,-11},{1994,7,1,0,0,0,-10},{1993,7,1,0,0,0, -9},{1992,7,1,0,0,0, -8},{1991,1,1,0,0,0, -7},{1990,1,1,0,0,0, -6},{1988,1,1,0,0,0, -5},{1985,7,1,0,0,0, -4},{1983,7,1,0,0,0, -3},{1982,7,1,0,0,0, -2},{1981,7,1,0,0,0, -1},{0}
};

• read_leaps_text()：从文件中读取跳秒，以GPST形式的epoch时间给

• rewind(fp) ：将文件内部的位置指针重新指向一个流的开头

• define MAXLEAPS 64

• strchr()：字符串查找

static int read_leaps_text(FILE *fp)
{char buff[256],*p;int i,n=0,ep[6],ls;rewind(fp);while (fgets(buff,sizeof(buff),fp)&&n<MAXLEAPS) {if ((p=strchr(buff,'#'))) *p='\0';if (sscanf(buff,"%d %d %d %d %d %d %d",ep,ep+1,ep+2,ep+3,ep+4,ep+5,&ls)<7) continue;    //格式化读取跳秒的epoch时间for (i=0;i<6;i++) leaps[n][i]=ep[i]; //写入跳秒的epoch时间leaps[n++][6]=ls;   //写入跳秒时间改正数}return n;
}

• read_leaps_usno() ：

• USNO：美国海军天文台

static int read_leaps_usno(FILE *fp)
{static const char *months[]={"JAN","FEB","MAR","APR","MAY","JUN","JUL","AUG","SEP","OCT","NOV","DEC"};double jd,tai_utc;char buff[256],month[32],ls[MAXLEAPS][7]={{0}};int i,j,y,m,d,n=0;rewind(fp);while (fgets(buff,sizeof(buff),fp)&&n<MAXLEAPS) {if (sscanf(buff,"%d %s %d =JD %lf TAI-UTC= %lf",&y,month,&d,&jd,&tai_utc)<5) continue;if (y<1980) continue;for (m=1;m<=12;m++) if (!strcmp(months[m-1],month)) break;if (m>=13) continue;ls[n][0]=y;ls[n][1]=m;ls[n][2]=d;ls[n++][6]=(char)(19.0-tai_utc);}for (i=0;i<n;i++) for (j=0;j<7;j++) {leaps[i][j]=ls[n-i-1][j];}return n;
}

• read_leaps()：会调用read_leaps_text()、read_leaps_usno

/* read leap seconds table -----------------------------------------------------
* read leap seconds table
* args   : char    *file    I   leap seconds table file
* return : status (1:ok,0:error)
* notes  : The leap second table should be as follows or leapsec.dat provided
*          by USNO.
*          (1) The records in the table file cosist of the following fields:
*              year month day hour min sec UTC-GPST(s)
*          (2) The date and time indicate the start UTC time for the UTC-GPST
*          (3) The date and time should be descending order.
*-----------------------------------------------------------------------------*/
extern int read_leaps(const char *file)
{FILE *fp;int i,n;if (!(fp=fopen(file,"r"))) return 0;/* read leap seconds table by text or usno */if (!(n=read_leaps_text(fp))&&!(n=read_leaps_usno(fp))) {fclose(fp);return 0;}for (i=0;i<7;i++) leaps[n][i]=0.0;fclose(fp);return 1;
}

二、坐标系统

void ecef2pos(const double *r, double *pos);
void pos2ecef(const double *pos, double *r);
void ecef2enu(const double *pos, const double *r, double *e);
void enu2ecef(const double *pos, const double *e, double *r);
void covenu  (const double *pos, const double *P, double *Q);
void covecef (const double *pos, const double *Q, double *P);
void xyz2enu (const double *pos, double *E);
void eci2ecef(gtime_t tutc, const double *erpv, double *U, double *gmst);
void deg2dms (double deg, double *dms, int ndec);
double dms2deg(const double *dms);

全球定位系统的最基本任务是确定用户在空间的位置。而所谓用户的位置， 实际上是指该用户在特定坐标系的位置坐标，位置是相对于参考坐标系而言的， 为此，首先要设立适当的坐标系。坐标系统是由原点位置、3个坐标轴的指向和 尺度所定义，根据坐标轴指向的不同，可划分为两大类坐标系：天球坐标系和地 球坐标系。由于坐标系相对于时间的依赖性，每一类坐标系又可划分为若干种不同定义 的坐标系。 不管采用什么形式，坐标系之间通过坐标平移、旋转和尺度转换， 可以将一个坐标系变换到另一个坐标系去。

1、基础理论知识

参考博客： GNSS原理与应用（三）——坐标系统与时间系统、 GPS从入门到放弃三 --- GPS坐标系
参考书籍：武大《导航学》课本

1. 大地水准面与地球椭球

• 水准面：海水在重力作用下，呈静止状态，形成的重力等位面（不规则、可以很多）。

• 大地水准面：平均海平面向陆地延伸（不规则，只有一个），不能作为计算和制图的基准面。

• 地球形状：两极稍扁、赤道略鼓 ，北极稍凸、南极稍凹的类似梨形的形体，横切面接近一个圆，纵切面接近一个椭圆，近视一个旋转椭球。

• 地球椭球：椭圆绕其短半轴旋转一周形成旋转椭球，确定一个子午圈即可确定一个地球椭球。用地球椭球代替地球表面，作为计算和制图的基准面。

• 总地球椭球：与全球大地水准面吻合的旋转椭球。

• 参考椭球：用局部资料推算出的地球椭球。

• 椭球定位：确定大地水准面与椭球面的相对关系，使椭球面与地球密合。

• 椭球定向：使旋转椭球短半轴，平行和重合。

1. 天球的基本概念

• 天球：以地球质心为球心，以无穷远为半径形成的球体。

• 天轴：地球自转轴的延伸。

• 天极：天轴与天球表面的交点。

• 天球赤道面：过地球质心与天轴垂直的平面。

• 天球赤道：天球表面与天球赤道面的交线（圈）。

• 时圈：过天轴的平面与天球表面的交线（圈）。

• 黄道：地球公转平面与天球表面的交线（圈）。

• 黄赤交角：天球（地球）赤道面与黄道面的夹角。

• 黄极：过地球质心垂直于黄道面的直线，与天球表面的交点。

• 秋分点：太阳在黄道面上运动（逆时针旋转），由北向南，运动到天球赤道与黄道的交点。

1. 空间直角坐标系与大地坐标系

• 空间直角坐标系XYZ：

• X纵轴表示南北、Y横轴表示东西，XY互换可使用所有三角公式。

• z轴与椭球短半轴重合指向北极N

• x轴为起始大地子午面与椭球赤道面交线

• 大地坐标系BLH

1. 天球坐标系与地球坐标系

• 天球坐标系：坐标系指向不变，方便描述卫星运动。

• 地球坐标系：坐标系随地球自转，方便描述地球上的位置。

1. 参心坐标系与地心坐标系、站心坐标系

• 参心坐标系：原点在参心（参考椭球）

• 地心坐标系：原点在地心（总地球椭球）

• 站心坐标系：原点在测站

1. 岁差、章动、极移

• 岁差：由于天球赤道和天球黄道的长期运动而导致的春分点的进动 ，北天极绕北黄极顺时针转动，周期为25800年。

岁差模型：IAU1976（L77）、IAU2000、IAU2006（P03）、B03、fF03

• 章动：由于月球、太阳和各大行星与地球间的相对位置存在周期性变化，因此作用在地球赤道隆起部分的力矩也在变化，地月系质心绕日公转的轨道面也存在周期性摄动，因此在岁差的基础上还存在各种大小和周期各不相同的微小周期性变化。 瞬时北天极围绕瞬时北黄极旋转，大致成椭圆形状，周期为18.6年。

章动模型：IAU1980、IAU2000
精确模型IAU2000A，简化模型IAU2000B，精确模型精度0.2mas、简化模型精度1mas，对GPS来说1mas引起13cm的卫星位置误差

不改正岁差与章动影响： 瞬时真
改正章动影响： 瞬时平
改正岁差与章动影响： 协议

• 极移：由于地球表面的物质运动（如洋流、海潮等）以及地球内部的物质运动（如地幔的运动），会使极点的位置产生变化 ，极点的位置产生变化。

1. 国际天球坐标参考系ITRS即其参考框架ICRF：国际天球参考系ICRS由国际地球自转服务IERS所建立的国际天球参考框架ICEF来实现的。ICRF框架中坐标轴是指向由甚长基线干涉VLBI所确定的一组河外射电源（控制），在J2000.0的天球赤道来予以定义和维持的。

根据质心选太阳系质心和地球质心分为质心天球参考系（BCRS）和地心天球参考系（GCRS）

1. 国际地球坐标参考系ITRS及其参考框架ITRF：ITRF是由一组IERS测站的坐标，站坐标的年变化率，及相应的地球定向参数EOP实现的。IGS的精密星历就采用这一框架。

WGS-84有时视为一个坐标系统，有时视为一个参考框架，WGS84满足ITRS的规定，理论上说WGG84与ITRF、ITRS一致。WGS-84（BLH）主要用于导航定位、ITRS主要用于大地测量和地球动力学研究。

2、常用坐标系

定位就需要坐标， 坐标当然是相对坐标系而言的，我们描述一个物体的位置，首先就需要建立坐标系。按大类来分，坐标系可以分为 惯性坐标系和非惯性坐标系。惯性坐标系是在空间静止或者做匀速直线运动的坐标系，其他都是非惯性坐标系。GPS涉及到的坐标系大体有五个。

1. 地心惯性坐标系（ECI: Earth Centered Inertial）

• 地心惯性坐标系是太阳系内的一个惯性坐标系，不随地球而转动，也不受地球、太阳运行的章动和岁差的影响。

• 坐标原点位于地心；X轴位于赤道平面内，指向某一特定年(历元时刻)的太阳春分点位置；Z轴指向那一年地球北极的平均位置处；Y轴位于赤道平面内，与X轴垂直，且与X、Z轴构成右手直角坐标系。

• 由于采用的历元时间不同，可以有各种不同的地心惯性坐标系，目前国际上通用的地心惯性坐标系是J2000历元坐标系，它是以公元2000年的春分点为基准的历元坐标系。

1. 地心地固直角坐标系（ECEF: Earth Centered Earth Fixed）

• 地固坐标系固定在地球上而随地球一起在空间做公转和自转运动，因此地球上任一固定点在地球坐标系的坐标就不会由于地球旋转而变化。

• 坐标原点位于地心；X轴指向参考子午面与地球赤道的交点；Z轴与地球自转轴重合并指向地球北极；Y轴位于赤道平面内，与X轴垂直，且与X、Z轴构成右手直角坐标系。

• 因为有极移，所以采用了协议地极，以1900年到1905年间的地极实际位置的平均值作为基准点。

1. 大地坐标系：也叫经纬高坐标系（LLA: Longitude Latitude Altitude）

• 也是地固坐标系。坐标原点位于地心。

• 基于基准椭球体（基准椭球体是定义的与地球几何最吻合的椭球体）。

• 大地纬度 ϕ \phiϕ 是过该点的基准椭球面法线与赤道面的夹角。纬度值在-90°到+90°之间。北半球为正，南半球为负。

• 大地经度 λ \lambdaλ 是过该点的子午面与本初子午面之间的夹角。经度值在-180°到+180°之间。

• 大地高度 h hh 是过该点到基准椭球面的法线距离，基准椭球面以内为负，以外为正。

1. 站心坐标系：也叫东北天坐标系（ENU: East North Up）

• 是以观测站为原点的坐标系，主要用于了解以观察者为中心的其他物体运动规律。

• 三个坐标轴分别指向相互垂直的东向、北向和天向，因而又称东北天坐标系。

• 可用于计算卫星在用户处的观测向量、仰角和方位角。

1. WGS-84: World Geodetic System-1984 Coordinate System

CGCS2000坐标系和WGS84坐标系的区别与联系

• 是一个地心地固直角坐标系。

• 坐标原点为地心，Z轴指向国际时间服务机构（BIH）1984年定义的协议地球极（CTP: Conventional Terrestrial Pole）方向，X轴指向本初子午面和CTP赤道的交点，Y轴与Z轴、X轴垂直构成右手坐标系。

• GPS广播星历是以WGS-84坐标系为基准的。

3、GNSS定位（SPP、RTK、PPP）位置坐标系

摘录自博客： GNSS定位（SPP、RTK、PPP）位置坐标系

通常GNSS定位算法可以输出各种坐标系下的定位结果（大地坐标系LLA、当地坐标系NED、地球固定坐标系ECEF），但是算法内部通常采用ECEF坐标系进行计算。ECEF坐标系的种类有很多，通常大多数算法中默认为WGS84坐标系，而实际各种定位算法的定位结果究竟在哪种ECEF坐标系中呢？

1. 单点定位SPP：由计算公式可以看出，单点定位中定位结果的坐标系，取决于由星历计算出来的卫星ECEF位置的坐标系。通过看各个卫星系统ICD，或者搜索就可以知道GNSS参考系统。

• GPS星历所计算出来的卫星位置是WGS84坐标系；

• GLONASS星历计算出来的卫星位置是PZ-90坐标系；

• GALILEO星历计算出来的卫星位置是GTRE坐标系；

• BDS星历计算出来的卫星位置是CGCS2000坐标；

因此如果是用单系统进行计算，那么计算出来的位置就位于相应的GNSS参考系。比如只用GPS卫星进行计算，那么定位位置在WGS84坐标系中。不过由于本身广播星历所计算出来的卫星位置误差就有几米到几十米的误差，单点定位的精度本身也是米级，这个量级已经大于了坐标系之间的误差。所以多个系统一起进行单点定位，即使认为单点定位位置是在WGS84坐标系下，也是可以的，这一点在RTKLIB的用户手册中也有提及（具体可参见其E.2 Coordiantes System）。

1. 差分定位RTK：无论是伪距差分，还是载波相位差分，实际上是在计算基线向量。在基站位置上，加上基线向量，从而得到用户位置。

在差分定位中，差分定位位置的ECEF坐标系取决于基站的坐标系。那卫星位置的坐标系没有影响吗？有影响，但是非常小。在差分定位中，我们会利用卫星位置来计算LOS（line of sight）。LOS的分母是用户位置到卫星位置之间的距离，分子是用户位置和卫星位置ECEF三个轴分量的差值。如果按卫星高度2万公里算（分母），坐标转换误差即使是10米，结果也是10E-7。即使再乘以基线，误差也最多是毫米级。不同的Network或者不同CORS站，它们的基站位置通常在不同坐标系下。在进行差分定位时，由于我们需要达到厘米级的定位精度，因此我们需要注意基站的坐标系。

1. 精密单点定位ppp：和单点定位相似，PPP的定位结果坐标系取决于精密星历中卫星位置的ECEF坐标系。在精密星历文件的第一行会标注所采用的坐标系。由于精密星历所用的坐标系和WGS-84差别很小，所以很多时候不需要转换。

4、RTKLIB中坐标系统函数

RTKLIB内部中，运算使用的是ECEF坐标系统。

• dms2deg()：度分秒dms—>度deg

deg2dms()：度deg—>度分秒dms

extern void deg2dms(double deg, double *dms, int ndec)
{double sign=deg<0.0?-1.0:1.0,a=fabs(deg);double unit=pow(0.1,ndec);dms[0]=floor(a); a=(a-dms[0])*60.0;dms[1]=floor(a); a=(a-dms[1])*60.0;dms[2]=floor(a/unit+0.5)*unit;if (dms[2]>=60.0) {dms[2]=0.0;dms[1]+=1.0;if (dms[1]>=60.0) {dms[1]=0.0;dms[0]+=1.0;}}dms[0]*=sign;
}

extern double dms2deg(const double *dms)
{double sign=dms[0]<0.0?-1.0:1.0;return sign*(fabs(dms[0])+dms[1]/60.0+dms[2]/3600.0);
}

• ECEF地心地固直角坐标系与大地坐标系LLA互转

RTKLIB的源码中的pos2ecf和ecf2pos函数的计算过程的理论公式

• pos2ecef()：大地坐标（lon,lat,h）转地心空间直角坐标（x,y,z）

• pos：{lat,lon,h} (rad,m)

• r：输出参数：{x,y,z} (m)

extern void pos2ecef(const double *pos, double *r)
{double sinp=sin(pos[0]),cosp=cos(pos[0]),sinl=sin(pos[1]),cosl=cos(pos[1]);double e2=FE_WGS84*(2.0-FE_WGS84),v=RE_WGS84/sqrt(1.0-e2*sinp*sinp);r[0]=(v+pos[2])*cosp*cosl;r[1]=(v+pos[2])*cosp*sinl;r[2]=(v*(1.0-e2)+pos[2])*sinp;
}

• ecef2pos()： 地心空间直角坐标（x,y,z）转大地坐标（lon,lat,h）

extern void ecef2pos(const double *r, double *pos)
{double e2=FE_WGS84*(2.0-FE_WGS84),r2=dot(r,r,2),z,zk,v=RE_WGS84,sinp;for (z=r[2],zk=0.0;fabs(z-zk)>=1E-4;) {zk=z;sinp=z/sqrt(r2+z*z);v=RE_WGS84/sqrt(1.0-e2*sinp*sinp);z=r[2]+v*e2*sinp;}pos[0]=r2>1E-12?atan(z/sqrt(r2)):(r[2]>0.0?PI/2.0:-PI/2.0);pos[1]=r2>1E-12?atan2(r[1],r[0]):0.0;pos[2]=sqrt(r2+z*z)-v;
}

• ECEF地心地固直角坐标系与ENU站心坐标系互转

• xyz2enu()：计算将ECEF中的向量转换到站心坐标系中的转换矩阵。

• pos：{lat,lon} (rad)

• E：33转换矩阵

extern void xyz2enu(const double *pos, double *E)
{double sinp=sin(pos[0]),cosp=cos(pos[0]),sinl=sin(pos[1]),cosl=cos(pos[1]);E[0]=-sinl;      E[3]=cosl;       E[6]=0.0;E[1]=-sinp*cosl; E[4]=-sinp*sinl; E[7]=cosp;E[2]=cosp*cosl;  E[5]=cosp*sinl;  E[8]=sinp;
}

• enu2ecef()：地方坐标(N,E,U)转ECEF坐标（x,y,z）。*参数中要输入(N,E,U)以及其大地坐标(lon,lat)。

extern void enu2ecef(const double *pos, const double *e, double *r)
{double E[9];xyz2enu(pos,E);matmul("TN",3,1,3,1.0,E,e,0.0,r);
}

• ecef2enu()：ECEF坐标（x,y,z）转地方坐标(N,E,U)。*参数中要输入(X,Y,Z)以及其大地坐标(lon,lat)。 地方坐标(N,E,U)也就地方正切坐标。

extern void ecef2enu(const double *pos, const double *r, double *e)
{double E[9];xyz2enu(pos,E);matmul("NN",3,1,3,1.0,E,r,0.0,e);
}

• covecef()：将地方坐标（N,E,U）转换为ECEF坐标的协方差阵

• 先调用xyz2enu()算转换矩阵E，再用协方差传播定律

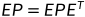
extern void covecef(const double *pos, const double *Q, double *P)
{double E[9],EQ[9];xyz2enu(pos,E);matmul("TN",3,3,3,1.0,E,Q,0.0,EQ);matmul("NN",3,3,3,1.0,EQ,E,0.0,P);
}

• covenu()：将ECEF坐标的协方差阵，转换为地方坐标（N,E,U）的协方差阵

extern void covenu(const double *pos, const double *P, double *Q)
{double E[9],EP[9];xyz2enu(pos,E);matmul("NN",3,3,3,1.0,E,P,0.0,EP);matmul("NT",3,3,3,1.0,EP,E,0.0,Q);
}

• ECI地心惯性坐标系与ECEF地心地固直角坐标系转换

导航卫星定轨在惯性系ECI完成，之后还需要转换到地固系ECEF
参考博客： ITRS 与 GCRS 之间的坐标转换
IAU1976_1980及2000A岁差章动模型的比较
RTKLIB里用的好像是1976岁差模型和1980章动模型

• Rx、Ry、Rz坐标旋转矩阵

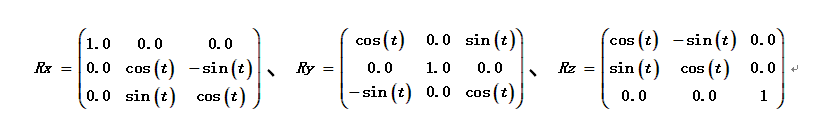
#define Rx(t,X) do { \(X)[0]=1.0; (X)[1]=(X)[2]=(X)[3]=(X)[6]=0.0; \(X)[4]=(X)[8]=cos(t); (X)[7]=sin(t); (X)[5]=-(X)[7]; \
} while (0)#define Ry(t,X) do { \(X)[4]=1.0; (X)[1]=(X)[3]=(X)[5]=(X)[7]=0.0; \(X)[0]=(X)[8]=cos(t); (X)[2]=sin(t); (X)[6]=-(X)[2]; \
} while (0)#define Rz(t,X) do { \(X)[8]=1.0; (X)[2]=(X)[5]=(X)[6]=(X)[7]=0.0; \(X)[0]=(X)[4]=cos(t); (X)[3]=sin(t); (X)[1]=-(X)[3]; \
} while (0)

• eci2ecef()：求ECI坐标(x,y,z)转ECEF坐标(x,y,z)的转换矩阵。

• fabs()：对浮点数取绝对值

• fmod()：用于查找除法的余数，它接受两个数字(分子和分母)，并返回四舍五入为零的分子/分母的浮点余数

extern void eci2ecef(gtime_t tutc, const double *erpv, double *U, double *gmst)
{const double ep2000[]={2000,1,1,12,0,0};static gtime_t tutc_;       //带_:静态变量，保存上一次调用时的值static double U_[9],gmst_;gtime_t tgps;double eps,ze,th,z,t,t2,t3,dpsi,deps,gast,f[5];double R1[9],R2[9],R3[9],R[9],W[9],N[9],P[9],NP[9];int i;trace(4,"eci2ecef: tutc=%s\n",time_str(tutc,3));if (fabs(timediff(tutc,tutc_))<0.01) { /* read cache */for (i=0;i<9;i++) U[i]=U_[i];if (gmst) *gmst=gmst_; return;}tutc_=tutc;/* terrestrial time */  //地面时间tgps=utc2gpst(tutc_);t=(timediff(tgps,epoch2time(ep2000))+19.0+32.184)/86400.0/36525.0;t2=t*t; t3=t2*t;/* astronomical arguments */ast_args(t,f);/* iau 1976 precession */   //岁差ze=(2306.2181*t+0.30188*t2+0.017998*t3)*AS2R;th=(2004.3109*t-0.42665*t2-0.041833*t3)*AS2R;z =(2306.2181*t+1.09468*t2+0.018203*t3)*AS2R;eps=(84381.448-46.8150*t-0.00059*t2+0.001813*t3)*AS2R;Rz(-z,R1); Ry(th,R2); Rz(-ze,R3);matmul("NN",3,3,3,1.0,R1,R2,0.0,R);matmul("NN",3,3,3,1.0,R, R3,0.0,P); /* P=Rz(-z)*Ry(th)*Rz(-ze) *//* iau 1980 nutation */     //章动nut_iau1980(t,f,&dpsi,&deps);Rx(-eps-deps,R1); Rz(-dpsi,R2); Rx(eps,R3);matmul("NN",3,3,3,1.0,R1,R2,0.0,R);matmul("NN",3,3,3,1.0,R ,R3,0.0,N); /* N=Rx(-eps)*Rz(-dspi)*Rx(eps) *//* greenwich aparent sidereal time (rad) */ //格林威治视恒星时gmst_=utc2gmst(tutc_,erpv[2]);gast=gmst_+dpsi*cos(eps);gast+=(0.00264*sin(f[4])+0.000063*sin(2.0*f[4]))*AS2R;/* eci to ecef transformation matrix */Ry(-erpv[0],R1); Rx(-erpv[1],R2); Rz(gast,R3);matmul("NN",3,3,3,1.0,R1,R2,0.0,W );matmul("NN",3,3,3,1.0,W ,R3,0.0,R ); /* W=Ry(-xp)*Rx(-yp) */matmul("NN",3,3,3,1.0,N ,P ,0.0,NP);matmul("NN",3,3,3,1.0,R ,NP,0.0,U_); /* U=W*Rz(gast)*N*P */for (i=0;i<9;i++) U[i]=U_[i];if (gmst) *gmst=gmst_; trace(5,"gmst=%.12f gast=%.12f\n",gmst_,gast);trace(5,"P=\n"); tracemat(5,P,3,3,15,12);trace(5,"N=\n"); tracemat(5,N,3,3,15,12);trace(5,"W=\n"); tracemat(5,W,3,3,15,12);trace(5,"U=\n"); tracemat(5,U,3,3,15,12);
}