本文主要是介绍Python-Level5-day05:二分类支持向量机模型及其三种核函数实现线性分类方法,水果分类案例,朴素贝叶斯实现分类原理及其案例实现,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、支持向量机
1. 基本概念
1)什么是支持向量机
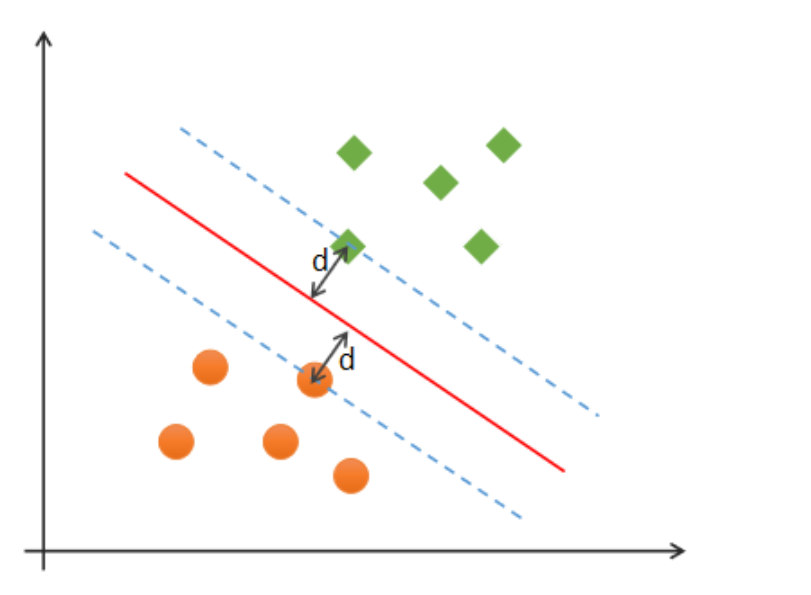
支持向量机(Support Vector Machines)是一种二分类模型,在机器学习、计算机视觉、数据挖掘中广泛应用,主要用于解决数据分类问题,它的目的是寻找一个超平面(高维度空间下的线性模型)来对样本进行分割,分割的原则是间隔最大化(即数据集的边缘点到分界线的距离2d最大化,如下图),最终转化为一个凸二次规划问题来求解。通常SVM用于二元分类问题,对于多元分类可将其分解为多个二元分类问题,再进行分类。所谓“支持向量”,就是下图中虚线穿过的边缘点。支持向量机就对应着能将数据正确划分并且间隔最大的直线(下图中红色直线)。找到一个向量支持起来两边点分类就是支持向量机,只考虑离分界最近点分类线画好,其他自然分类好。
![]()
2)最优分类边界
什么才是最优分类边界?什么条件下的分类边界为最优边界呢?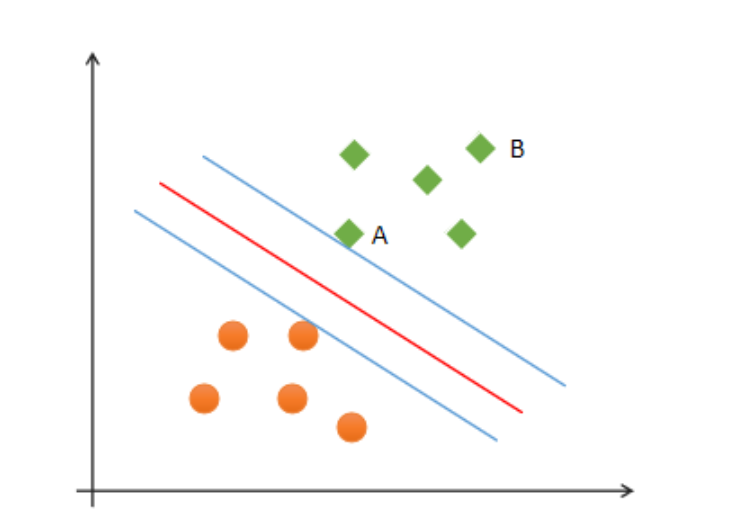
![]() 编辑
编辑
如图中的A,B两个样本点,B点被预测为正类的确信度要大于A点,所以SVM的目标是寻找一个超平面,使得离超平面较近的异类点之间能有更大的间隔,即不必考虑所有样本点,只需让求得的超平面使得离它近的点间隔最大。超平面可以用如下线性方程来描述:
$$
w^T x + b = 0
$$
其中,x=(x_1;x_2;...;x_n),w=(w_1;w_2;...;w_n),b为偏置项. 可以从数学上证明,支持向量到超平面距离为:
$$
\gamma = \frac{1}{||w||}
$$
为了使距离最大,只需最小化||w||即可.
3)SVM最优边界要求
SVM寻找最优边界时,需满足以下几个要求:
(1)正确性:对大部分样本都可以正确划分类别;
(2)安全性:支持向量,即离分类边界最近的样本之间的距离最远;
(3)公平性:支持向量与分类边界的距离相等;
(4)简单性:采用线性方程(直线、平面)表示分类边界,也称分割超平面。如果在原始维度中无法做线性划分,那么就通过升维变换,在更高维度空间寻求线性分割超平面. 从低纬度空间到高纬度空间的变换通过核函数进行。
4)线性可分与线性不可分
① 线性可分
如果一组样本能使用一个线性函数将样本正确分类,称这些数据样本是线性可分的。那么什么是线性函数呢?在二维空间中就是一条直线,在三维空间中就是一个平面,以此类推,如果不考虑空间维数,这样的线性函数统称为超平面。
② 线性不可分
如果一组样本,无法找到一个线性函数将样本正确分类,则称这些样本线性不可分。以下是一个一维线性不可分的示例: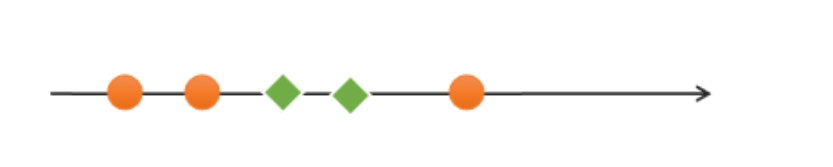
![]()
一维线性不可分
以下是一个二维不可分的示例: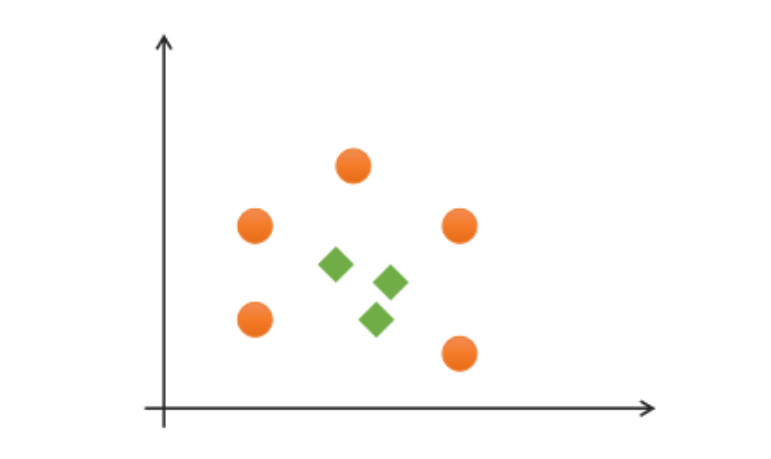
![]() 编
编
二维线性不可分
对于该类线性不可分问题,可以通过升维,将低纬度特征空间映射为高纬度特征空间,实现线性可分,如下图所示: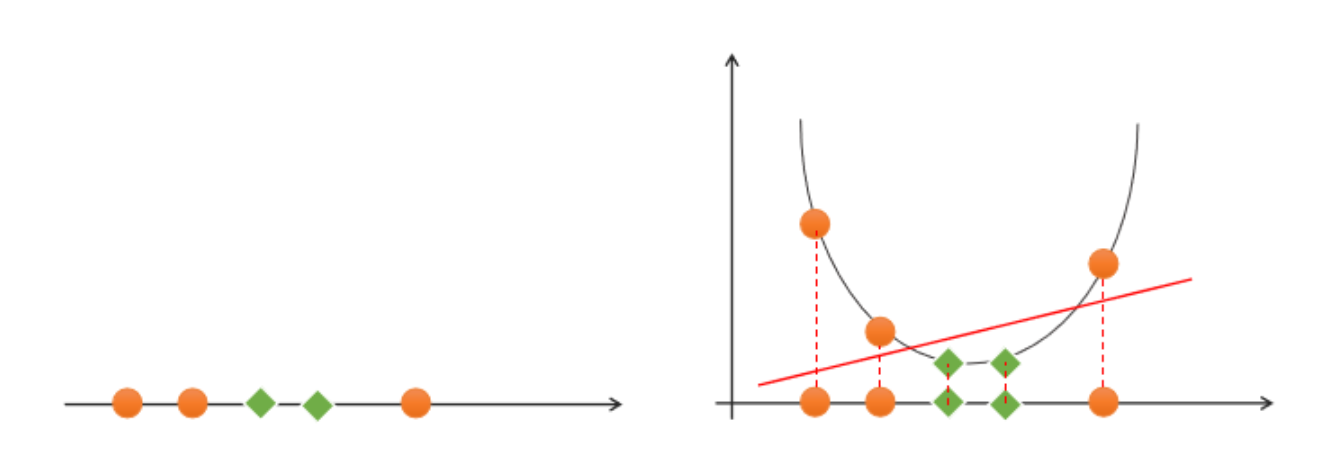
![]()
一维空间升至二维空间实现线性可分
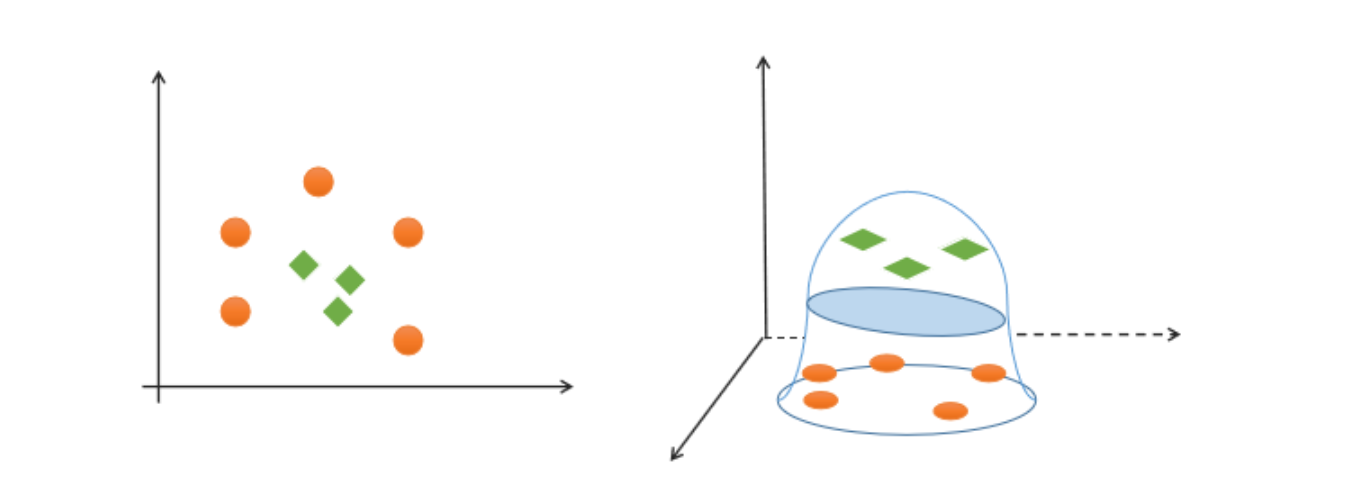
![]()
二维空间升至三维空间实现线性可分
那么如何实现升维?这就需要用到核函数。后面神经网络采用的增加线条的方式进行分类,没有进行升维度。升级维度举例子就是如果你从长相上区分不了双胞胎,就从打乒乓球左右手不同的维度区分。
2. 核函数
通过名为核函数的特征变换,增加新的特征,使得低纬度线性不可分问题变维高纬度线性可分问题。如果低维空间存在K(x,y),x,y∈Χ,使得K(x,y)=ϕ(x)·ϕ(y),则称K(x,y)为核函数,其中ϕ(x)·ϕ(y)为x,y映射到特征空间上的内积,ϕ(x)为X→H的映射函数。以下是几种常用的核函数。
支持向量机5句话总结:1.是一个二分类模型(可以多分类);2.寻找线性分类边界;3.只考虑离分类边界最近样本;4.求间隔2d最大化;5.对于线性不可分,通过核函数升维方式转化线性可分。神经网络分类慢慢替代了它。6.三个核函数种类。
1)线性核函数
线性核函数(Linear)表示不通过核函数进行升维,仅在原始空间寻求线性分类边界,主要用于线性可分问题。
示例代码:
# 支持向量机示例
import numpy as np
import sklearn.model_selection as ms
import sklearn.svm as svm
import sklearn.metrics as sm
import matplotlib.pyplot as mp
x, y = [], []
with open("../data/multiple2.txt", "r") as f:for line in f.readlines():data = [float(substr) for substr in line.split(",")]x.append(data[:-1]) # 输入y.append(data[-1]) # 输出
# 列表转数组
x = np.array(x)
y = np.array(y, dtype=int)
# 线性核函数支持向量机分类器
model = svm.SVC(kernel="linear") # 线性核函数
# model = svm.SVC(kernel="poly", degree=3) # 多项式核函数
# print("gamma:", model.gamma)
# 径向基核函数支持向量机分类器
# model = svm.SVC(kernel="rbf",
# gamma=0.01, # 概率密度标准差
# C=200) # 概率强度
model.fit(x, y)
# 计算图形边界
l, r, h = x[:, 0].min() - 1, x[:, 0].max() + 1, 0.005
b, t, v = x[:, 1].min() - 1, x[:, 1].max() + 1, 0.005
# 生成网格矩阵
grid_x = np.meshgrid(np.arange(l, r, h), np.arange(b, t, v))
flat_x = np.c_[grid_x[0].ravel(), grid_x[1].ravel()] # 合并
flat_y = model.predict(flat_x) # 根据网格矩阵预测分类
grid_y = flat_y.reshape(grid_x[0].shape) # 还原形状
mp.figure("SVM Classifier", facecolor="lightgray")
mp.title("SVM Classifier", fontsize=14)
mp.xlabel("x", fontsize=14)
mp.ylabel("y", fontsize=14)
mp.tick_params(labelsize=10)
mp.pcolormesh(grid_x[0], grid_x[1], grid_y, cmap="gray")
C0, C1 = (y == 0), (y == 1)
mp.scatter(x[C0][:, 0], x[C0][:, 1], c="orangered", s=80)
mp.scatter(x[C1][:, 0], x[C1][:, 1], c="limegreen", s=80)
mp.show()
![]()
绘制图形: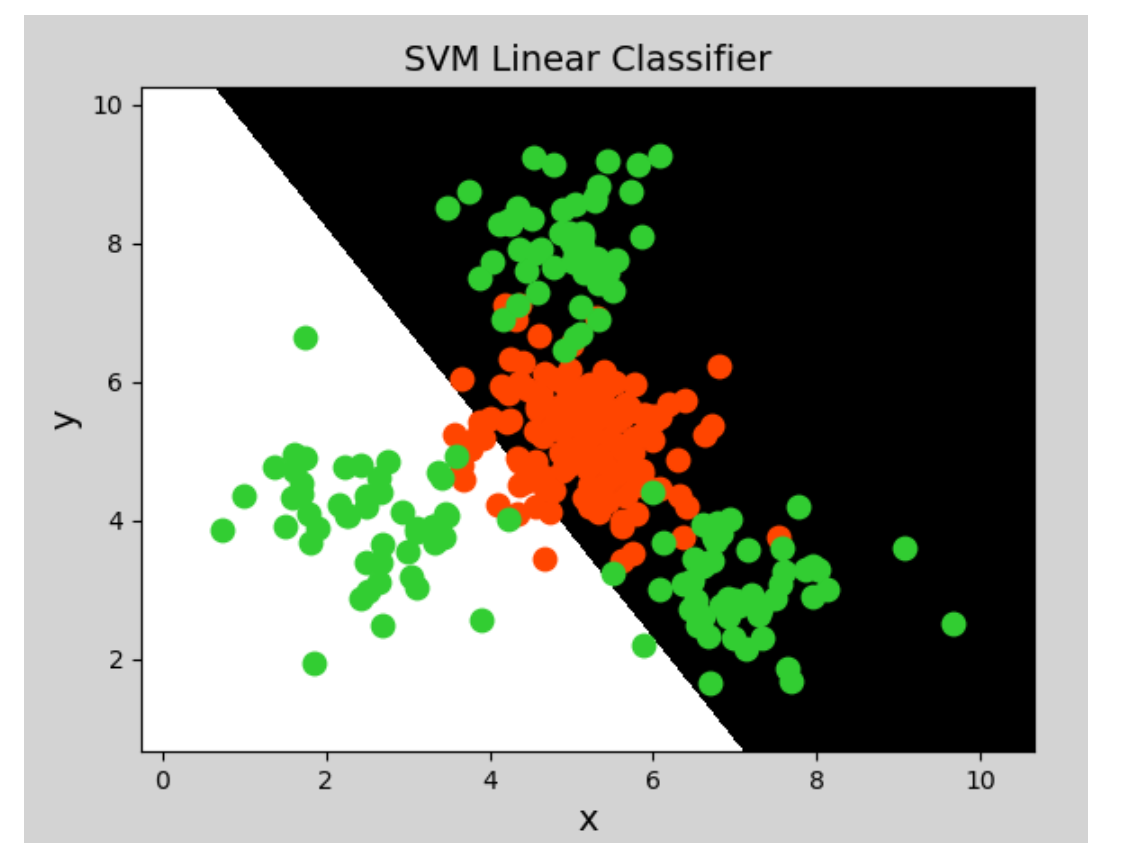
![]() 编辑
编辑
2)多项式核函数
多项式核函数(Polynomial Kernel)用增加高次项特征的方法做升维变换,当多项式阶数高时复杂度会很高,其表达式为:
$$
K(x,y)=(αx^T·y+c)d
$$
其中,α表示调节参数,d表示最高次项次数,c为可选常数。分类边界的模型依然是线性模型,可能是高维度下线性模型。
示例代码(将上一示例中创建支持向量机模型改为一下代码即可):
model = svm.SVC(kernel="poly", degree=3) # 多项式核函数
![]()
生成图像: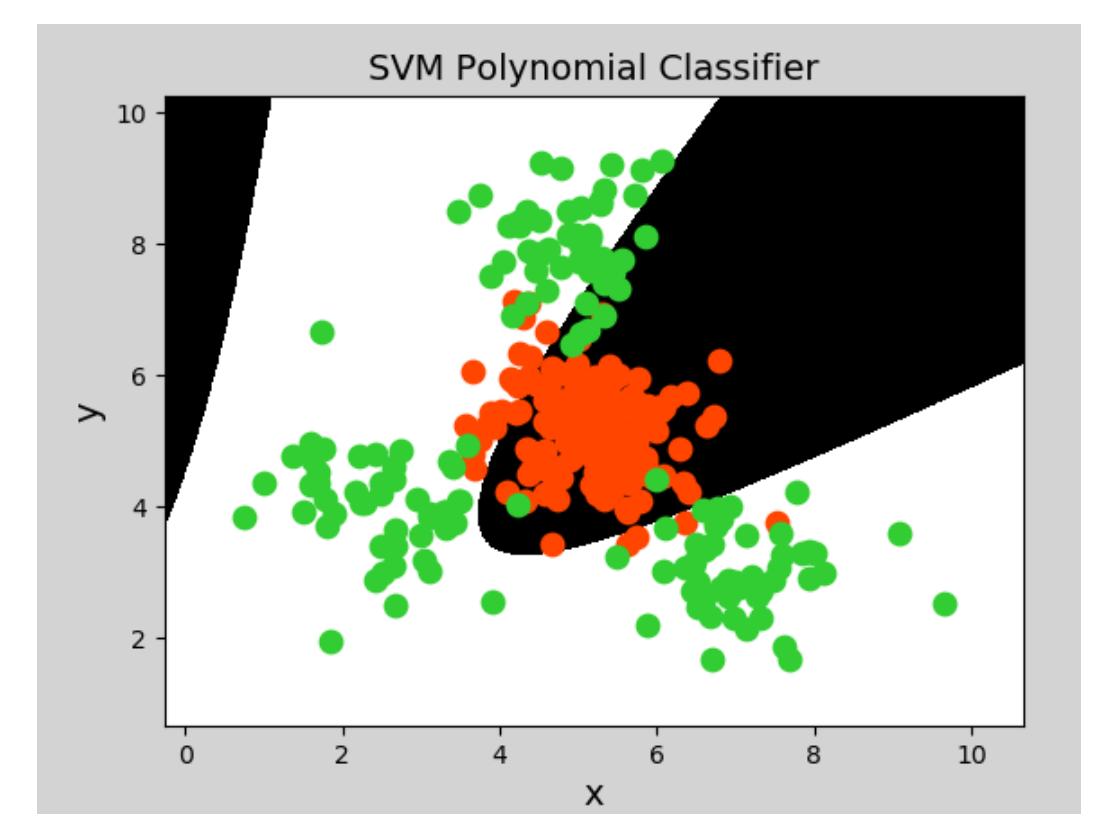
![]()
3)径向基核函数
径向基核函数(Radial Basis Function Kernel)具有很强的灵活性,应用很广泛。与多项式核函数相比,它的参数少,因此大多数情况下,都有比较好的性能。在不确定用哪种核函数时,可优先用它。由于类似于高斯函数,所以也称其为高斯核函数。表达式如下: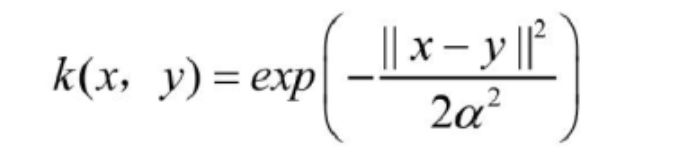
![]()
其中,α^2越大,高斯核函数变得越平滑,即得到一个随输入x变化较缓慢,模型的偏差和方差大,泛化能力差,容易过拟合。α^2越小,高斯核函数变化越剧烈,模型的偏差和方差越小,模型对噪声样本比较敏感。
示例代码(将上一示例中分类器模型改为如下代码即可):
# 径向基核函数支持向量机分类器 model = svm.SVC(kernel="rbf",gamma=0.01, # 概率密度标准差C=600) # 概率强度,该值越大对错误分类的容忍度越小,分类精度越高,但泛化能力越差;该值越小,对错误分类容忍度越大,但泛化能力强
![]()
生成图像:分类边界的模型依然是线性模型,可能是高维度下线性模型。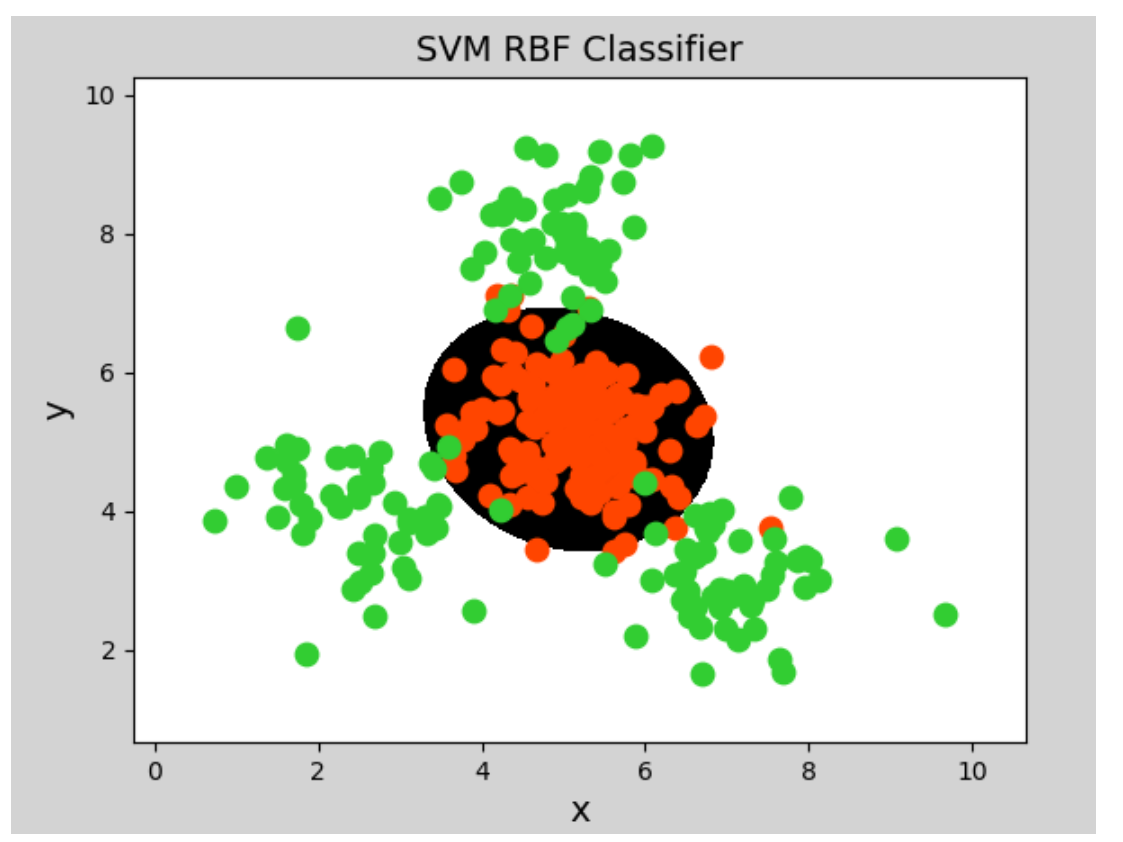
![]()
3. 总结
(1)支持向量机是二分类模型
(2)支持向量机通过寻找最优线性模型作为分类边界
(3)边界要求:正确性、公平性、安全性、简单性
(4)可以通过核函数将线性不可分转换为线性可分问题,核函数包括:线性核函数、多项式核函数、径向基核函数
(5)支持向量机适合少量样本的分类
传统机器学习是人制定算法提取特征,深度学习是模型提取。因此特征值提取直接决定分类器分出的准确率,前期先用支持向量机分类器,后期直接用神经网络分类。人工的特征提取算法也很难以理解,提取强特征,舍弃弱特征。
# 02_fruits_svm_demo.py
# 利用SVM实现图像分类
"""人工算法提取出128个特征放入分类器训练。
图像分类原理:先对图片进行特征提取(实现数据降维度,留下强特征,不是所有特征都有用)形成特征图或者特征向量,把特征图给分类模型(支持向量机)分类产生分类结果。整个过程特征提取与分类器模型最重要特征提取到深度学习阶段直接卷积神经网络提取,不用人工算法提取,及其的复杂
"""
import os
import numpy as np
import cv2 as cv
import sklearn.metrics as sm
import sklearn.preprocessing as sp
import sklearn.svm as svm
# 名称和数字的对应关系,打标签
name_dict = {"apple": 0, "banana": 1, "grape": 2}
# 遍历样本目录,将图像路径存、类别入字典中(图像标注,打标签)
def search_samples(dir_path): # 参数为样本目录路径img_samples = {} # key-名称 value-图像路径列表
dirs = os.listdir(dir_path) # 列出目录下所有内容for d in dirs:# 拼接子目录完整路径sub_dir_path = dir_path + "/" + dif not os.path.isdir(sub_dir_path): # 不是目录continue
imgs = os.listdir(sub_dir_path) # 列出子目录下的内容for img_file in imgs: # 遍历文件# 拼接完整图像文件路径img_path = sub_dir_path + "/" + img_file# 将图片路径存入字典if d in img_samples: # 类别已经存在,直接添加img_samples[d].append(img_path)else: # 类别不存在,先创建空列表,再添加img_list = []img_list.append(img_path)img_samples[d] = img_listreturn img_samples # 返回字典
# 遍历训练集
train_samples = search_samples("../data/fruits_tiny/train")
# print(train_samples)
# 根据路径读取图像数据,并提取特征,把特征值放入train_x,作为输入,类别标签为train_y,有监督学习
train_x, train_y = [], []
for label, img_list in train_samples.items():for img_file in img_list: # 遍历每个列表中的图像路径# 读取图像数据 以前在平面下特征是二维的,这里就是128维度了,没有本质上区别。print("读取图像:", img_file) # 图像数据本质是3通道矩阵,对矩阵进行特征提取得到128维度特征向量im = cv.imread(img_file) # 读取im_gray = cv.cvtColor(im, # 图像数据cv.COLOR_BGR2GRAY) # 转灰度图# 缩放统一大小:一般不影响图像内容质量h, w = im_gray.shape[:2] # 取出高度、宽度f = 200 / min(h, w) # 计算缩放比率im_gray = cv.resize(im_gray, None,fx=f, fy=f) # x,y方向的缩放比率# 计算图像特征提取sift = cv.xfeatures2d.SIFT_create()keypoints = sift.detect(im_gray) # 检测关键点_, desc = sift.compute(im_gray, keypoints) # 计算特征值print(desc.shape)
# 每行相加, 特征矩阵合并(降维)成了特征向量(长度128),原特征矩阵是n行128列数据,你可以打印形状来看# 该特征向量作为模型的输入desc = np.sum(desc, axis=0)train_x.append(desc) # 添加到输入train_y.append(name_dict[label]) # 类别数组加入到输出
# 列表转数组
train_x = np.array(train_x)
train_y = np.array(train_y)
print("开始训练......")
model = svm.SVC(kernel="poly", degree=2) # SVM分类器
model.fit(train_x, train_y)
print("训练结束.")
# 测试模型
test_samples = search_samples('../data/fruits_tiny/test')
test_x, test_y = [], []
# 读取测试数据,并计算特征值
for label, filenames in test_samples.items():descs = np.array([])
for img_file in filenames:print("读取测试样本:", img_file)
# 读取原始图像,并转为灰度图像image = cv.imread(img_file)gray = cv.cvtColor(image, cv.COLOR_BGR2GRAY)
# 调整大小h, w = gray.shape[:2]f = 200 / min(h, w)gray = cv.resize(gray, None, fx=f, fy=f)
# 计算特征矩阵sift = cv.xfeatures2d.SIFT_create()keypoints = sift.detect(gray)_, desc = sift.compute(gray, keypoints)
# 添加测试输入、输出数组desc = np.sum(desc, axis=0) # 0-列方向test_x.append(desc)test_y.append(name_dict[label]) # 标签
test_x = np.array(test_x)
test_y = np.array(test_y)
# 使用测试集的数据执行预测
print("开始预测......")
pred_test_y = model.predict(test_x)
print("预测结束.")
# 打印分类报告
print(sm.classification_report(test_y, pred_test_y))
一、朴素贝叶斯
朴素贝叶斯是一组功能强大且易于训练的分类器,它使用贝叶斯定理来确定给定一组条件的结果的概率预测需要的概率,“朴素”的含义是指所给定的条件都能独立存在和发生. 朴素贝叶斯是多用途分类器,能在很多不同的情景下找到它的应用,例如垃圾邮件过滤、自然语言处理等.
1. 概率
1)定义
概率是反映随机事件出现的可能性大小. 随机事件是指在相同条件下,可能出现也可能不出现的事件. 例如:
(1)抛一枚硬币,可能正面朝上,可能反面朝上,这是随机事件. 正/反面朝上的可能性称为概率;
(2)掷骰子,掷出的点数为随机事件. 每个点数出现的可能性称为概率;
(3)一批商品包含良品、次品,随机抽取一件,抽得良品/次品为随机事件. 经过大量反复试验,抽得次品率越来越接近于某个常数,则该常数为概率.
我们可以将随机事件记为A或B,则P(A), P(B)表示事件A或B的概率.
2)联合概率与条件概率
① 联合概率
指包含多个条件且所有条件同时成立的概率,记作P ( A , B ) ,或P(AB),或P(A \bigcap B)
② 条件概率
已知事件B发生的条件下,另一个事件A发生的概率称为条件概率,记为:P(A|B)
③ 事件的独立性
事件A不影响事件B的发生,称这两个事件独立,记为:
$$
P(AB)=P(A)P(B)
$$
因为A和B不相互影响,则有:
$$
P(A|B) = P(A)
$$
可以理解为,给定或不给定B的条件下,A的概率都一样大.
3)先验概率与后验概率
① 先验概率
先验概率也是根据以往经验和分析得到的概率,例如:在没有任何信息前提的情况下,猜测对面来的陌生人姓氏,姓李的概率最大(因为全国李姓为占比最高的姓氏),这便是先验概率.由因求果
② 后验概率
后验概率是指在接收了一定条件或信息的情况下的修正概率,例如:在知道对面的人来自“牛家村”的情况下,猜测他姓牛的概率最大,但不排除姓杨、李等等,这便是后验概率.现在拉肚子是吃瓜导致吗 由果求因。
③ 两者的关系
事情还没有发生,求这件事情发生的可能性的大小,是先验概率(可以理解为由因求果:喝凉水拉肚子可能性). 事情已经发生,求这件事情发生的原因是由某个因素引起的可能性的大小,是后验概率(由果求因:来肚子由于喝凉水概率). 先验概率与后验概率有不可分割的联系,后验概率的计算要以先验概率为基础.
2. 贝叶斯定理
1)定义
贝叶斯定理由英国数学家托马斯.贝叶斯 ( Thomas Bayes)提出,用来描述两个条件概率之间的关系,定理描述为:
$$
P(A|B) = \frac{P(A)P(B|A)}{P(B)}
$$
其中,P(A)和P(B)是A事件和B事件发生的概率. P(A|B)称为条件概率,表示B事件发生条件下,A事件发生的概率. 推导过程:
$$
P(A,B) =P(B)P(A|B)\\ P(B,A) =P(A)P(B|A)
$$
其中P(A,B)称为联合概率,指事件B发生的概率,乘以事件A在事件B发生的条件下发生的概率. 因为P(A,B)=P(B,A), 所以有:
$$
P(B)P(A|B)=P(A)P(B|A)
$$
两边同时除以P(B),则得到贝叶斯定理的表达式. 其中,P(A)是先验概率,P(A|B)是已知B发生后A的条件概率,也被称作后验概率.
2)贝叶斯定理示例
【示例一】计算诈骗短信的概率
| 事件 | 概率 | 表达式 |
|---|---|---|
| 所有短信中,诈骗短信 | 5% | P(A)= 0.05 |
| 所有短信中,含有“中奖”两个字 | 4% | P(B)= 0.04 |
| 所有短信中,是诈骗短信,并且含有“中奖”两个字 | 50% | P(B|A) = 0.5 |
求:收到一条新信息,含有“中奖”两个字,是诈骗短信的概率?
P(A|B) = P(A) P(B|A) / P(B) = 0.05 * 0.5 / 0.04 = 0.625
【示例二】计算喝酒驾车的概率
| 事件 | 概率 | 表达式 |
|---|---|---|
| 所有客人中,驾车 | 20% | P(A)= 0.2 |
| 所有客人中,喝酒 | 10% | P(B)= 0.1 |
| 所有客人中,开车并且喝酒 | 5% | P(B|A)= 0.05 |
求:喝过酒仍然会开车的人的比例是多少?
P(A|B) = P(A) P(B|A) / P(B) = 0.2 * 0.05 / 0.1 = 0.1
3. 朴素贝叶斯分类器
1)分类原理
朴素贝叶斯分类器就是根据贝叶斯公式计算结果进行分类的模型,“朴素”指事件之间相互独立无影响. 例如:有如下数据集:
| Text | Category |
|---|---|
| A great game(一个伟大的比赛) | Sports(体育运动) |
| The election was over(选举结束) | Not sports(不是体育运动) |
| Very clean match(没内幕的比赛) | Sports(体育运动) |
| A clean but forgettable game(一场难以忘记的比赛) | Sports(体育运动) |
| It was a close election(这是一场势均力敌的选举) | Not sports(不是体育运动) |
求:”A very close game“ 是体育运动的概率?如果是决策树就根据样本相似性划分到哪一个类别,但这里数据集不是样本。就需要贝叶斯定理。数学上表示为 P(Sports | a very close game). 根据贝叶斯定理,实现分类。是运动的概率可以表示为:
$$
P(Sports | a \ very \ close \ game) = \frac{P(a \ very \ close \ game | sports) * P(sports)}{P(a \ very \ close \ game)}
$$
不是运动概率可以表示为:
$$
P(Not \ Sports | a \ very \ close \ game) = \frac{P(a \ very \ close \ game | Not \ sports) * P(Not \ sports)}{P(a \ very \ close \ game)}
$$
概率更大者即为分类结果. 由于分母相同,即比较分子谁更大即可. 我们只需统计”A very close game“ 多少次出现在Sports类别中,就可以计算出上述两个概率. 但是”A very close game“ 并没有出现在数据集中,所以这个概率为0,要解决这个问题,就假设每个句子的单词出现都与其它单词无关(事件独立即朴素的含义),所以,P(a very close game)可以写成:
$$
P(a \ very \ close \ game) = P(a) * P(very) * P(close) * P(game)
$$
$$
P(a \ very \ close \ game|Sports)= \\ P(a|Sports)*P(very|Sports)*P(close|Sports)*P(game|Sports)
$$
统计出“a", "very", "close", "game"出现在"Sports"类别中的概率,就能算出其所属的类别. 具体计算过程如下:
-
第一步:计算总词频:Sports类别词语总数11,Not Sports类别词语总数9,词语总数14
-
第二步:计算每个类别的先验概率
# Sports和Not Sports概率 P(Sports) = 3 / 5 = 0.6 P(Not Sports) = 2 / 5 = 0.4 # Sports条件下各个词语概率 P(a | Sports) = (2 + 1) / (11 + 14) = 0.12 P(very | Sports) = (1 + 1) / (11 + 14) = 0.08 P(close | Sports) = (0 + 1) / (11 + 14) = 0.04 P(game | Sports) = (2 + 1) / (11 + 14) = 0.12 # Not Sports条件下各个词语概率 P(a | Not Sports) = (1 + 1) / (9 + 14) = 0.087 P(very | Not Sports) = (0 + 1) / (9 + 14) = 0.043 P(close | Not Sports) = (1 + 1) / (9 + 14) = = 0.087 P(game | Not Sports) = (0 + 1) / (9 + 14) = 0.043
其中,分子部分加1,是为了避免分子为0的情况;分母部分都加了词语总数14,是为了避免分子增大的情况下计算结果超过1的可能.
-
第三步:将先验概率带入贝叶斯定理,计算概率:
是体育运动的概率:
$$
P(a \ very \ close \ game|Sports) * P(Sport)= \\ P(a|Sports)*P(very|Sports)*P(close|Sports)*P(game|Sports)*P(Sports)= \\ 0.12 * 0.08 * 0.04 * 0.12 * 0.6 = 0.000027648
$$
不是体育运动的概率:
$$
P(a \ very \ close \ game|Not \ Sports) * P(Not Sport)= \\ P(a|Not \ Sports)*P(very|Not \ Sports)*P(close|Not \ Sports)*P(game|Not \ Sports)*P( NotSports)= \\ 0.087 * 0.043 * 0.087 * 0.043 * 0.4 = 0.0000055984
$$
分类结果:P(Sports) = 0.000027648 , P(Not Sports) = 0.0000055984, 是体育运动.
2)实现朴素贝叶斯分类器
在sklearn中,提供了三个朴素贝叶斯分类器,分别是:
-
GaussianNB(高斯朴素贝叶斯分类器):适合用于样本的值是连续的,数据呈正态分布的情况(比如人的身高、城市家庭收入、一次考试的成绩等等)
-
MultinominalNB(多项式朴素贝叶斯分类器):适合用于大部分属性为离散值的数据集
-
BernoulliNB(伯努利朴素贝叶斯分类器):适合用于特征值为二元离散值或是稀疏的多元离散值的数据集
该示例中,样本的值为连续值,且呈正态分布,所以采用GaussianNB模型. 代码如下:
# 朴素贝叶斯分类示例
# 朴素贝叶斯:通过贝叶斯定理,假设事件的出现是独立的,
# 计算给定某个条件下,属于某个类别的概率
import numpy as np
import sklearn.naive_bayes as nb
import matplotlib.pyplot as mp
# 输入,输出
x, y = [], []
# 读取数据文件
with open("../data/multiple1.txt", "r") as f:for line in f.readlines():data = [float(substr) for substr in line.split(",")]x.append(data[:-1]) # 输入样本:取从第一列到倒数第二列y.append(data[-1]) # 输出样本:取最后一列
x = np.array(x)
y = np.array(y, dtype=int)
# 创建高斯朴素贝叶斯分类器对象
model = nb.GaussianNB()
model.fit(x, y) # 训练
# 计算显示范围
left = x[:, 0].min() - 1
right = x[:, 0].max() + 1
buttom = x[:, 1].min() - 1
top = x[:, 1].max() + 1
grid_x, grid_y = np.meshgrid(np.arange(left, right, 0.01),np.arange(buttom, top, 0.01))
mesh_x = np.column_stack((grid_x.ravel(), grid_y.ravel()))
mesh_z = model.predict(mesh_x)
mesh_z = mesh_z.reshape(grid_x.shape)
mp.figure('Naive Bayes Classification', facecolor='lightgray')
mp.title('Naive Bayes Classification', fontsize=20)
mp.xlabel('x', fontsize=14)
mp.ylabel('y', fontsize=14)
mp.tick_params(labelsize=10)
mp.pcolormesh(grid_x, grid_y, mesh_z, cmap='gray')
mp.scatter(x[:, 0], x[:, 1], c=y, cmap='brg', s=80)
mp.show()
执行结果: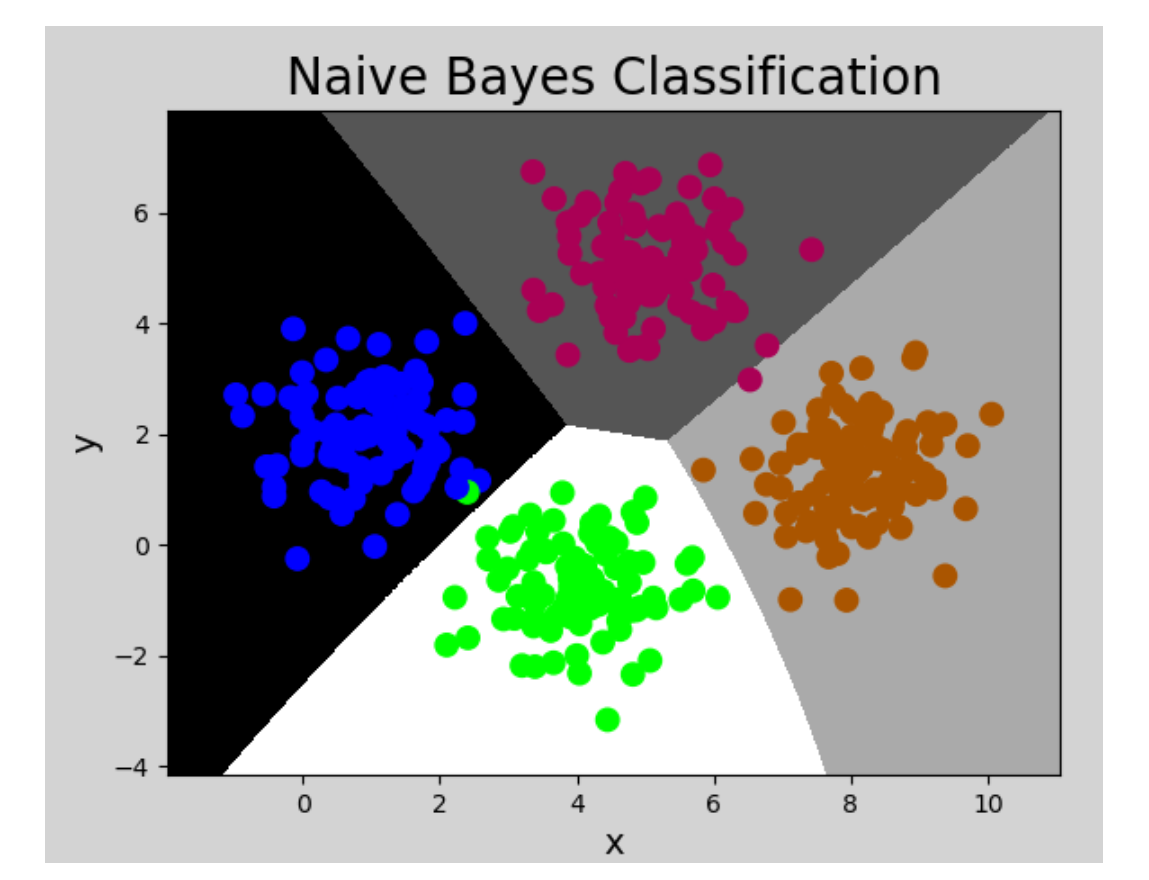
![]()
4. 总结
1)什么是朴素贝叶斯:朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法。“朴素”的含义为:假设问题的特征变量都是相互独立地作用于决策变量的,即问题的特征之间都是互不相关的。
2)朴素贝叶斯分类的特点
① 优点
-
逻辑性简单
-
算法较为稳定。当数据呈现不同的特点时,朴素贝叶斯的分类性能不会有太大的差异。
-
当样本特征之间的关系相对比较独立时,朴素贝叶斯分类算法会有较好的效果。
② 缺点
-
特征的独立性在很多情况下是很难满足的,因为样本特征之间往往都存在着相互关联,如果在分类过程中出现这种问题,会导致分类的效果大大降低。
3)什么情况下使用朴素贝叶斯:根据先验概率计算后验概率的情况,且样本特征之间独立性较强即朴素。
这篇关于Python-Level5-day05:二分类支持向量机模型及其三种核函数实现线性分类方法,水果分类案例,朴素贝叶斯实现分类原理及其案例实现的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



