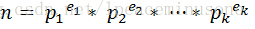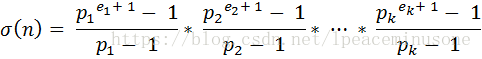LightOJ - 1336 Sigma Function （因子和）

Sigma function is an interesting function in Number Theory. It is denoted by the Greek letter Sigma (σ). This function actually denotes the sum of all divisors of a number. For example σ(24) = 1+2+3+4+6+8+12+24=60. Sigma of small numbers is easy to find but for large numbers it is very difficult to find in a straight forward way. But mathematicians have discovered a formula to find sigma. If the prime power decomposition of an integer is

Then we can write,

For some n the value of σ(n) is odd and for others it is even. Given a value n, you will have to find how many integers from 1 to n have even value of σ.


Input
Input starts with an integer T (≤ 100), denoting the number of test cases.


Each case starts with a line containing an integer n (1 ≤ n ≤ 1012).


Output
For each case, print the case number and the result.


Sample Input
4
3
10
100
1000
Sample Output
Case 1: 1
Case 2: 5
Case 3: 83

Case 4: 947

https://blog.csdn.net/strangedbly/article/details/50908522

#include<map>
#include<stack>
#include<queue>
#include<math.h>
#include<vector>
#include<string>
#include<stdio.h>
#include<iostream>
#include<string.h>
#include<algorithm>
#define mem(a,b) memset(a,b,sizeof(a))
#define maxn 1100000
#define maxm 1000000000005
#define mod 1000000007
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
int main(){int t,test=0;scanf("%d",&t);while(t--){ll n;scanf("%lld",&n);ll ans=0;ans=(ll)sqrt(n*1.0);ans+=(ll)sqrt(n/2.0);printf("Case %d: %lld\n",++test,n-ans);}
}