本文主要是介绍Smartcard中T0协议等待时间WT的定义和计算,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Smartcard测试中,基本上都包含有对等待时间WT(waiting time)的极限测试,在客户支持中,也常常遇到WT不能通过测试的问题,大部分情况是由于卡通信中WT没有正确设置的缘故。
本来想将所有的关于WT的东西都列出来,包括GT, WT, CWT, BWT, BGT等,懒散了一下,这里只说T0协议下WT的计算。
本文推理和计算中涉及到ISO-7816标准和一些数学公式,会让人没有那么赖心看下去,如果你只关心结论,请跳转到:
- 第2.3节,看关于等待时间WT的一些结论
- 第3节,查看T0卡通信时解析ATR并计算工作等待时间WT的实例
这里所有关于时间的定义都来自标准ISO/IEC 7816-3:2006(E)
ISO/IEC 7816-3:2006(E)
Identification cards — Integrated circuit cards — Part 3:
Cards with contacts — Electrical interface and transmission protocols
1. 等待时间WT的定义
第7.2 Character frame中定义了GT和WT

这里指出:
1. 两个连续字符之间最小的上升沿间隔叫做”guart time”,记为GT。
2. 两个连续字符之间最大的上升沿间隔叫做”waiting time”,记为WT。
T0协议时关于WT,有两种:
1. 初始等待时间(initial waiting time,), 即复位应答ATR中的waiting time。
2. 工作等待时间(work waiting time),即卡通信时的waiting time。
下面来看看标准7816-3中关于这两个waiting time的规定。
2. T0卡复位和正常通信时的WT
2.1 复位时的WT
复位时发送ATR使用的WT又叫做初始等待时间(initial waiting time)
第8.1 Characters and coding conventions节指定了initial waiting time的值:

这里指出:
1. 复位传输ATR时,传输传输参数使用默认的Fd = 372, Dd = 1
2. 传输ATR时,GT = 12 etu, WT = 9600 etu
2.2 正常通信时的WT
正常通信时等待时间WT又叫做工作等待时间(work waiting time)
第10.2 Character level (page 28)节指定了T0协议的work waiting time的计算方式:

这里指出:
WT=WI×960×Fif W T = W I × 960 × F i f
其中:
1. WI参数从TC2的bit1~8解析得到,TC2的值0x00留作将来之用,如果TC2不存在,则WI默认为10
2. Fi和f参数可以从TA1解析拿到,bit5-8得到Fi和f,bit1-4得到Di,默认为Fi=372, f=5和Di=1,如下:
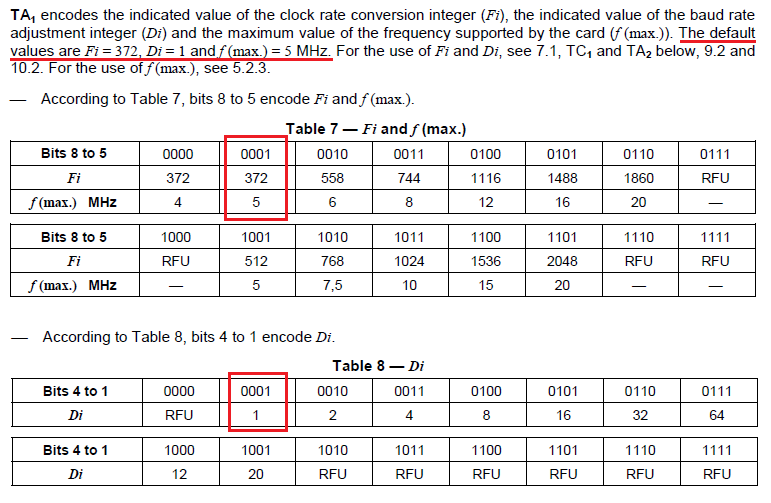
第7.1 Elementary time unit中定义了etu:

所以这里:
Fif=Di×1etu F i f = D i × 1 e t u
WT=WI×960×Fif=WI×960×Di×1etu W T = W I × 960 × F i f = W I × 960 × D i × 1 e t u
如果TC2不存在(WI=0),TA1不存在(Fi=371, f=5, Di=1)有:
WT=10×960×1×1etu=9600etu W T = 10 × 960 × 1 × 1 e t u = 9600 e t u
所以,T0协议工作时的WT和ATR的WT是一样的,都是9600etu。
2.3 WT结论
- ATR传输的
WT = 9600 etu; - T0卡工作时
WT = WI x Di x 960etu,默认情况下WI=10, Di=1,此时WT = 9600etu,跟ATR传输时一样。
3. 实例分析
3.1 卡1
某CA的T0卡发送的原始ATR为:
3B 34 94 00 30 42 30 30对ATR解析后的数据如下:
| - | - |
|---|---|
| TS = 0x3B | Direct Convention |
| T0 = 0x34 | Y(1): b0011, K: 4 (historical bytes) |
| TA(1) = 0x94 | Fi=512, Di=8, 64 cycles/ETU (62500 bits/s at 4.00 MHz, 78125 bits/s for fMax=5 MHz) |
| TB(1) = 0x00 | VPP is not electrically connected |
| Historical bytes | 30 42 30 30 |
| Category indicator byte: 0x30 | (proprietary format) “B00” |
这里存在TA1(Fi=512, f=5, Di=8),但不存在TC2(WI=10),因此WT:
WT=WI×Di×960etu=10×8×960etu=76800etu W T = W I × D i × 960 e t u = 10 × 8 × 960 e t u = 76800 e t u
所以在驱动中,需要将卡工作时的WT设置为76800etu,而不是默认的9600etu。
3.2 卡2
某CA的T0卡发送的原始ATR为:
3F 77 18 00 00 C2 EB 41 02 6C 90 00对ATR解析后的数据如下:
| - | - |
|---|---|
| TS = 0x3F | Inverse Convention |
| T0 = 0x77 | Y(1): b0111, K: 7 (historical bytes) |
| TA(1) = 0x18 | Fi=372, Di=12, 31 cycles/ETU (129032 bits/s at 4.00 MHz, 161290 bits/s for fMax=5 MHz) |
| TB(1) = 0x00 | VPP is not electrically connected |
| TC(1) = 0x00 | Extra guard time: 0 |
| Historical bytes | C2 EB 41 02 6C 90 00 |
| Category indicator byte: 0xC2 | (proprietary format) “.A.l..” |
这里存在TA1(Fi=372, f=5, Di=12),但不存在TC2(WI=10),因此WT:
WT=WI×Di×960etu=10×12×960etu=115200etu W T = W I × D i × 960 e t u = 10 × 12 × 960 e t u = 115200 e t u
所以在驱动中,需要将卡工作时的WT设置为115200etu,而不是默认的9600etu。
3.3 卡3
某CA的T0卡发送的原始ATR为:
3B 64 00 02 30 42 30 30对ATR解析后的数据如下:
| - | - |
|---|---|
| TS = 0x3B | Direct Convention |
| T0 = 0x64 | Y(1): b0110, K: 4 (historical bytes) |
| TB(1) = 0x00 | VPP is not electrically connected |
| TC(1) = 0x02 | Extra guard time: 2 |
| Historical bytes | 30 42 30 30 |
| Category indicator byte: 0x30 | (proprietary format) “B00” |
这里TA1和TC2都不存在,所以Fi, f, Di 和 WI都取默认值。
即:
Fi=372;f=5;Di=1;WI=10; F i = 372 ; f = 5 ; D i = 1 ; W I = 10 ;
WT=WI×Di×960etu=10×1×960etu=9600etu W T = W I × D i × 960 e t u = 10 × 1 × 960 e t u = 9600 e t u
所以在驱动中,卡工作时的WT跟ATR传输时的一样,都是9600etu。
4. ATR解析的福利
最后送上一个福利。
看了第3节,可见,计算etu的关键是要先解析收到的ATR,但你可能不了解7816-3标准,也不清楚ATR如何解析,那怎么办啊?
没有关系,一个名为“Smart card ATR parsing”的网站为你解析ATR,省了多少烦恼,我第一次发现的时候开心得不行。
好了,地址在:[Smart card ATR parsing] (https://smartcard-atr.appspot.com/)
赶快去体验吧!
这篇关于Smartcard中T0协议等待时间WT的定义和计算的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





