CSP 2021-04-2 邻域均值

2023-10-14 20:33

文章标签 csp 04 均值 2021 邻域

本文主要是介绍CSP 2021-04-2 邻域均值，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

问题描述
试题编号： 202104-2
试题名称：邻域均值
时间限制： 1.0s
内存限制： 512.0MB
在这里插入图片描述

样例输入

4 16 1 6
0 1 2 3
4 5 6 7
8 9 10 11
12 13 14 15

样例输出

样例输入

11 8 2 2
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 7 0 0 0 7 0 0 7 7 0
7 0 7 0 7 0 7 0 7 0 7
7 0 0 0 7 0 0 0 7 0 7
7 0 0 0 0 7 0 0 7 7 0
7 0 0 0 0 0 7 0 7 0 0
7 0 7 0 7 0 7 0 7 0 0
0 7 0 0 0 7 0 0 7 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0

样例输出

评测用例规模与约定

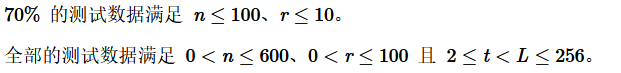
在这里插入图片描述

思路：

后三个测试数据挺大的，暴力最多解决前七个点，需要优化求解
用前缀和可以大大减少时间
（row1，row2）是每个点判断范围的行的范围
（line1，line2）是每个点判断范围的列的范围

ACWING上学的，可以用二维前缀和做，比一维前缀和又方便了很多，但还是要找到方框范围的起点终点的坐标

更新的AC代码：

#include<bits/stdc++.h>
using namespace std;
const int N = 610;
int d[N][N];
int n,L,r,t;
int sum[N][N];
int res = 0;
int main(){scanf("%d %d %d %d",&n,&L,&r,&t);int x;for(int i = 0;i < n;i++)for(int  j = 0;j < n;j++){scanf("%d",&x);sum[i][j] = x + sum[i-1][j] + sum[i][j-1]-sum[i-1][j-1];}int beginx,beginy,endx,endy;for(int i = 0;i < n;i++){for(int j = 0;j < n;j++){beginx = max(i-r,0);	//起点的坐标beginy = max(j-r,0);endx = min(i+r,n-1);	//终点的坐标endy = min(j+r,n-1);int num = (endx-beginx+1) * (endy-beginy+1);	//方框范围内的数字个数float cnt = 0;cnt = sum[endx][endy] - sum[endx][beginy-1] - sum[beginx-1][endy] + sum[beginx-1][beginy-1];	//二维前缀和cnt = (1.0)*cnt / num;if(cnt <= t)res++;}}printf("%d",res);		}

AC代码：

#include<bits/stdc++.h>
using namespace std;
int sum[1010][1010]={0};
int main(){ios::sync_with_stdio(false);int n,L,r,t;cin >> n >> L >> r >> t;int a[n+1][n+1];for(int i = 1;i <= n;i++){for(int j = 1;j <= n;j++){cin >> a[i][j];if(j == 1)sum[i][j] = a[i][j];else{sum[i][j] = a[i][j] + sum[i][j-1];}}}int line1,line2,row1,row2,cnt=0;for(int i = 1;i <= n;i++){for(int j = 1;j <= n;j++){row1 = i - r > 0 ? i-r : 1;row2 = i + r > n ? n : i+r;line1 = j - r > 0 ? j-r : 1;line2 = j + r > n ? n : j+r;int ans = 0;for(int k = row1;k <= row2;k++){if(line1==1)//如果范围第一列就是全矩阵第一列的话，直接累加sum[k][line2]ans += sum[k][line2];else ans += sum[k][line2] - sum[k][line1-1];}int num = (row2-row1+1)*(line2-line1+1);if(ans*1.0/num <= t){cnt++;}}}cout << cnt << endl;
}